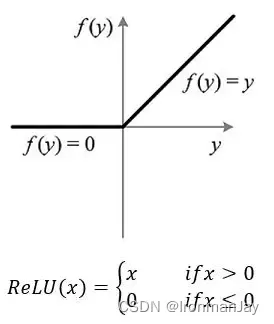基于CNN的MINIST手写数字识别项目代码以及原理详解
文章目录
- 项目简介
- 项目开发软件环境
- 项目开发硬件环境
- 前言
- 一、数据加载的作用
- 二、Pytorch进行数据加载所需工具
-
- 2.1 Dataset
- 2.2 Dataloader
- 2.3 Torchvision
- 2.4 Torchtext
- 2.5 加载项目需要使用的库
- 三、加载MINIST数据集
-
- 3.1 数据集简介
- 3.2 数据预处理
- 3.3 加载数据集
- 四、模型构建
- 五、CrossEntropyLoss
-
- 5.1 Softmax
- 5.2 Log
- 5.3 NLLLoss
- 六、优化器
- 七、模型训练
- 八、加载模型
- 九、模型测试
- 十、自定义手写数字识别测试
- 十一、项目结构图
- 十二、全部代码
- 总结
项目简介
本项目名为:基于CNN的MINIST手写数字识别项目。本项目完整的实现了MINIST手写数字的识别,模型的准确率高达 97 % 97\% 97%,损失率仅为 1 % 1\% 1%。利用训练好的模型去测试自定义手写数字,也可以准确识别!
项目开发软件环境
- Windows 11
- PyCharm 2022.1
- Python 3.7.0
- Matplotlib 3.1.1
- Torch 1.13.0
- Torchvision 0.14.0
- Pillow 6.2.0
- Numpy 1.17.2
项目开发硬件环境
- CPU:Intel® Core™ i7-8750H CPU @ 2.20GHz 2.20 GHz
- RAM:24GB
- GPU:NVIDIA GeForce GTX 1060
前言
本篇博文从整个项目数据集的导入到模型的构建以及最终的模型训练与测试和自定义手写数字识别,均进行了极为细致的代码分析。不仅如此,本文还将整个项目用到的所有技术以及知识点和原理都进行了极为详细的解释,利用图片以及公式力争将原理讲述的通俗易懂。通过本文,不仅可以学会手写数字识别项目的搭建过程,还可以搞懂CNN在手写数字识别项目中的应用以及背后的原理。当然,由于本人水平问题,可能有些问题解释的并不是很清晰,如有问题,还请读者与我反馈。最近也在学习这方面的知识点,读者感兴趣也可和我多交流!下面就正式开始本篇博文的内容!
一、数据加载的作用
因为在深度学习中,训练的数据通常数量十分巨大,不能一次性的把全部数据都传到模型中进行训练,所以要利用数据加载,将源数据的顺序打乱,进行分批和预处理后,最后将处理好的数据传给模型进行训练,这样才能保证模型训练的准确性。
通常情况下,加载好的数据一般每一行是一个训练样本,每一列为一个样本特征。
二、Pytorch进行数据加载所需工具
2.1 Dataset
Dataset是用来创建数据集的函数(一般称为数据集类),一般情况下,我们的数据集首先传给Dataset,封装为数据集类。可以使用Dataset自定义数据集的内容和标签,如何使用Dataset呢?只需要使用如下语句引入即可:
from torch.utils.data import Dataset
引入Dataset后,我们就可以自定义我们数据集的数据了。其实Dataset没什么复杂的,说白了就是将我们的数据集给规范化的封装起来了,需要使用的时候调用Dataset返回相应的数据信息即可。如果我们要自定义一个Dataset供我们使用,通常要完成以下三个函数(也可以不重写,直接调用,也可以返回数据集相应的信息):
__init__:初始化数据内容和标签
def __init__(self, Data, Label):
self.Data = Data
self.Label = Label
__getitem__:获取数据内容和标签
def __getitem__(self, index):
data = torch.Tensor(self.Data[index])
label = torch.Tensor(self.Label[index])
return data, label
__len__:获取数据集大小
def __len__(self):
return len(self.Data)
2.2 Dataloader
Dataloader又称为数据加载类,其作用是接收来自Dataset已经加载好的数据集,对原数据集进行顺序打乱、分批等操作。要使用Dataloader只需要使用如下语句引入即可:
from torch.utils.data import DataLoader
Dataloader的一些重要参数的含义如下:
- dataset:从Dataset中传入的原始数据集类
- batch_size:每批数据的大小
- shuffle:是否打乱数据集
- num_workers:工作的线程数
2.3 Torchvision
Torchvision是Pytorch的一个图形库,主要用来构建计算机视觉模型。其中主要API如下:
torchvision.models:包含常用的模型结构(包含预训练模型),例如AlexNet、VGG、ResNet等torchvision.datasets:一些加载数据的函数以及常用的数据集接口torchvision.transforms:常用的图片变换,例如裁剪、旋转等torchvision.utils:一些工具类
2.4 Torchtext
Torchtext是Pytorch处理文本的一个工具包。首先将不同类型的文件转换为Datasets,然后再将Dataset传向Iterator进行迭代、打包等其他处理。其中主要API如下:
torchtext.data.Example:表示一个样本、数据和标签torchtext.vocab.Vocab:表示词汇表,可以导入一些预训练词向量torchtext.data.Datasets:将文本数据封装为数据集类torchtext.datasets:包含常用的本文数据集torchtext.data.Iterator:用来生成batch的迭代器
2.5 加载项目需要使用的库
import matplotlib.pyplot as plt
import torch
from torchvision.datasets import MNIST
from torchvision import transforms
from torch.utils.data import DataLoader
from torch import nn
import os
from PIL import Image
import numpy as np
三、加载MINIST数据集
3.1 数据集简介
MINIST数据集由28×28灰度手写数字图像组成,共70000张图片,其中包括训练集图片60000张和测试集图片10000张,共有十个分类:0、1、2、3、4、5、6、7、8、9。
3.2 数据预处理
此步骤使用transforms将以下两步合并在一起,加载数据集的时候就按照此规则进行处理
-
将灰度图片像素值(0~255)转为Tensor(0~1),方便后续处理
-
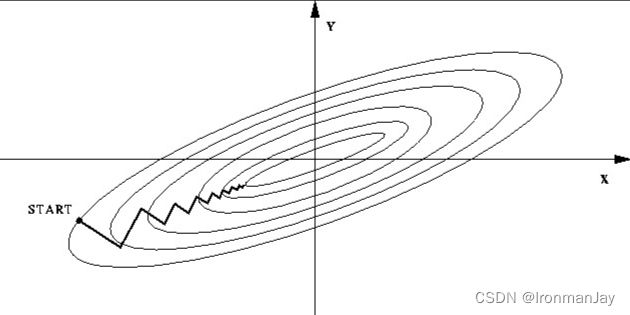
将数据归一化,即均值为0,标准差为1。关于归一化在梯度下降中的应用可见下两图,
由以上两图可见,数据归一化的优点包括:
- 加快梯度下降求最优解的速度
- 加快训练网络的收敛性
- 提高精度
可以使用以下Python代码实现将数据转为Tensor和归一化的预处理
# 预处理:将两个步骤整合在一起
transform = transforms.Compose({
transforms.ToTensor(), # 转为Tensor,范围改为0-1
transforms.Normalize((0.1307,),(0.3081)) # 数据归一化,即均值为0,标准差为1
})
3.3 加载数据集
我们可以使用如下代码加载数据集
# 训练数据集
train_data = MNIST(root='./data',train=True,download=True,transform=transform)
train_loader = DataLoader(train_data,shuffle=True,batch_size=64)
# 测试数据集
test_data = MNIST(root='./data',train=False,download=True,transform=transform)
test_loader = DataLoader(test_data,shuffle=False,batch_size=64)
这里的参数需要说明一下:
- root:表明加载的数据存储到哪里
- train:表示是否是训练集,如果是训练集,此参数就是True,反之(是验证集或训练集)就是False
- download:表明是否需要下载,如果需要下载,此参数就是True,反之(本地存在)就是False
- transform:指示加载的数据集应用的数据预处理的规则
当数据集加载好后,我们可以打印一下,发现已经成功加载数据集了。
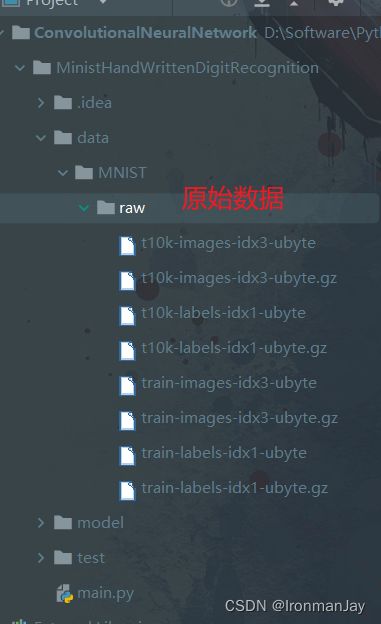
也可以看项目的目录,如下所示,可见数据已经加载完毕。
四、模型构建
# 模型
class Model(nn.Module):
def __init__(self):
super(Model,self).__init__()
self.linear1 = nn.Linear(784,256)
self.linear2 = nn.Linear(256,64)
self.linear3 = nn.Linear(64,10) # 10个手写数字对应的10个输出
def forward(self,x):
x = x.view(-1,784) # 变形
x = torch.relu(self.linear1(x))
x = torch.relu(self.linear2(x))
x = torch.relu(self.linear3(x))
return x
可以看到,共使用三层卷积层。因为每张图片的尺寸都是28,所以初始输入就是784个特征,经过三层卷积后,最终得到10分类,也就对应10种数字。
其中使用的激活函数为Relu激活函数,在此简单介绍一下Relu激活函数:
- Relu的全称为修正线性单元(Rectified Linear Unit) ,其函数图像如下所示,可以看到:
- 当 x < = 0 x <= 0 x<=0时, R e L U = 0 ReLU = 0 ReLU=0
- 当 x > 0 x > 0 x>0时, R e L U = x ReLU = x ReLU=x
-
Relu的导数图像如下图所示,可以看到:
- 当 x < = 0 x <= 0 x<=0时, R e L U ReLU ReLU的导数为 0 0 0
- 当 x > 0 x > 0 x>0时, R e L U ReLU ReLU的导数为 1 1 1
-
Relu的优点如下:
- 由Relu的原始图像和导数图像可知,Relu可能使部分神经元的值变为0,可以使神经元“死亡”,降低神经网络复杂性,从而有效缓解过拟合的问题
- 由于当 x > 0 x>0 x>0时,Relu的梯度恒为1,所以随着神经网络越来越复杂,不会导致梯度累乘后变得很大或很小,从而不会发生梯度爆炸或梯度消失问题
- Relu的计算非常简单,就是取0或者值本身,提高了神经网络的效率
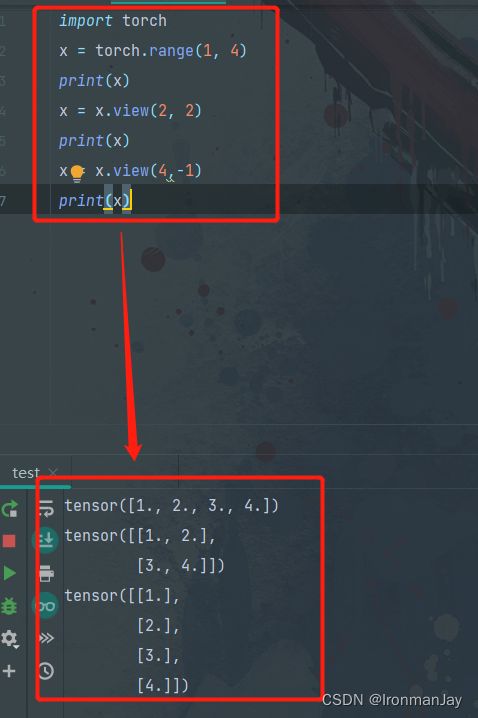
另外,还需要注意 v i e w ( ) view() view()这个函数,其目的是对tensor进行reshape,将向量铺平,可以看到,输入数据被解析为784维的特征,方便后续计算以及传入全连接层。关于 v i e w ( ) view() view()函数的用法可见如下示例:
五、CrossEntropyLoss
CrossEntropyLoss是手写数字分类问题的最后一步,其中主要包括三个步骤:
- Softmax
- Log
- NLLLoss
当我们构建好模型后,还需要对其进行损失判断以及优化,Pytorch中使用CrossEntropyLoss来完成以上步骤。下面会详细解释其中细节。
# CrossEntropyLoss
model = Model()
criterion = nn.CrossEntropyLoss() # 交叉熵损失,相当于Softmax+Log+NllLoss
5.1 Softmax
Softmax回归是一个线性多分类模型,在MINIST手写数字识别问题中,Softmax最终会给出预测值对于10个类别(0~9)出现的概率,最终模型的预测结果就是概率最大的类别。Softmax计算公式如下:
Softmax ( z i ) = exp ( z i ) ∑ j exp ( z j ) \operatorname{Softmax}\left(z_{i}\right)=\frac{\exp \left(z_{i}\right)}{\sum_{j} \exp \left(z_{j}\right)} Softmax(zi)=∑jexp(zj)exp(zi)
其中分子的 z i z_i zi是多分类中的第 i i i类的输出值,分母将所有类别的输出值求和,使用指数函数来将其转换为概率,最终将神经网络上一层的原始数据归一化到 [ 0 , 1 ] [0,1] [0,1],使用指数函数的原因是因为上一层的数据有正有负,所以使用指数函数将其变为大于0的值。具体转换过程如下图所示,可以通过判断哪类的输出概率最大,来判断最后的分类结果。
5.2 Log
经过Softmax后,还要将其结果取Log(对数),目的是将乘法转化为加法,从而减少计算量,同时保证函数的单调性,因为 l n ( x ) ln(x) ln(x)单调递增且:
l n ( x ) × l n ( y ) = l n ( x + y ) ln(x)×ln(y) = ln(x+y) ln(x)×ln(y)=ln(x+y)
5.3 NLLLoss
最终使用NLLLoss计算损失,损失函数定义为:
Loss ( Y ^ , Y ) = − Y log Y ^ \operatorname{Loss}(\hat{Y}, Y)=-Y \log \hat{Y} Loss(Y^,Y)=−YlogY^
其中的参数含义:
- Y ^ \hat{Y} Y^表示Softmax经过Log后的值
- Y Y Y为训练数据对应target的One-hot编码,表示此训练数据对应的target。
在这里简单提一嘴Ont-hot编码(独热编码)的概念,其实就是某个值有效,对应位置就是1,否则就是0,每一个One-hot编码对应一种状态,在手写数字识别中,可以使用One-hot的不同编码来分别对应每一种数字。
需要注意,此过程不需要手动进行One-hot编码,因为NLLLoss已经帮我们自动完成了,在训练计算损失的时候,它会自动的取出样本target值对应的下标位置,此位置在One-hot中为1,其余位置因为不表示,所以在One-hot中为0。整个过程如下图所示。
这样我们通过一系列的操作就得到了测试数据与target的损失值,后续就可以根据计算得到的损失值,去不断地迭代优化参数,直到损失值达到最低。
六、优化器
优化器使用的是SGD(随机梯度下降),学习率为0.8,学习率可能受到不同机器以及其他各方面的影响,会有所不同,不断调整多训练几次就好了。
optimizer = torch.optim.SGD(model.parameters(),0.8) # 第一个参数是初始化参数值,第二个参数是学习率
首先我们要明白什么是梯度下降算法,梯度下降算法是为了找到最优的参数值,使得损失函数最小,假设损失函数定义为:
J ( x ) = 1 n ∑ i = 1 n J ( x i ) J(x)=\frac{1}{n} \sum_{i=1}^{n} J\left(x_{i}\right) J(x)=n1i=1∑nJ(xi)
根据高等数学的知识可知,对于损失函数 J ( x ) J(x) J(x)来说, x x x是变量,要求损失函数 J ( x ) J(x) J(x)的最小值,应让损失函数 J ( x ) J(x) J(x)对 x x x求偏导,表示损失函数在 x x x处的梯度:
∇ J ( x ) = 1 n ∇ ∑ i = 1 n J ( x i ) \nabla J(x)=\frac{1}{n} \nabla \sum_{i=1}^{n} J\left(x_{i}\right) ∇J(x)=n1∇i=1∑nJ(xi)
然后更新 x x x:
x = x − ε ∇ J ( x ) x=x-\varepsilon\nabla J(x) x=x−ε∇J(x)
其中 ε \varepsilon ε就是我们常说的学习率,通过调整学习率最终得到最优的 x x x,使得:
∇ J ( x ) = 0 \nabla J(x)=0 ∇J(x)=0
此时梯度为0,说明已经达到极值点,也就是损失函数最小的点,此时的 x x x就是我们要求的最优参数。
那么这里为什么选用随机梯度下降算法作为优化器呢?因为我们的样本非常多,在进行参数优化时,如果对所有的样本都求梯度,那么开销会非常大,所以使用随机梯度算法,每次随机采样不同的少量样本进行参数优化,这样可以降低时间复杂度。
七、模型训练
到目前为止,我们已经完成了CrossEntropyLoss与优化器的定义,下面该准备训练模型了。
# 模型训练
def train():
for index,data in enumerate(train_loader):
input,target = data # input为输入数据,target为标签
optimizer.zero_grad() # 梯度清零
y_predict = model(input) # 模型预测
loss = criterion(y_predict,target) # 计算损失
loss.backward() # 反向传播
optimizer.step() # 更新参数
if index % 100 == 0: # 每一百次保存一次模型,打印损失
torch.save(model.state_dict(),"./model/model.pkl") # 保存模型
torch.save(optimizer.state_dict(),"./model/optimizer.pkl") # 保存优化器
print("损失值为:%.2f" % loss.item())
模型训练过程的步骤一般是固定的,主要包括:
-
获取训练数据以及其对于标签
测试的时候不需要数据对应的标签,但是训练的时候需要数据对应的标签,因为这样才能使用损失函数计算预测值与真实值之间的误差,从而最优化参数
-
梯度清零
因为训练的时候是分批次的,如果不设置梯度清零,就会将上一批次的梯度累加到当前批次,可能会造成模型预测不准确,所以每个批次都需要设置梯度清零
-
模型预测
利用之前建立好的模型对输入数据进行预测,得到预测值,其中包括最大预测值与其对应的数字下标
-
计算损失
利用之前创建好的CrossEntropyLoss计算损失值
-
反向传播
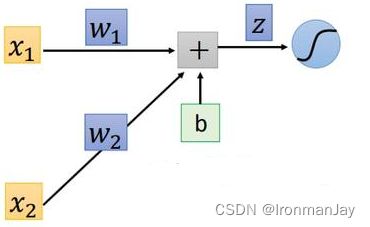
在这里简单介绍一些关于反向传播的内容,让我们以一个简单的神经网络中的神经元为例:
输入值会通过 z = w 1 x 1 + w 2 x 2 + b z=w_1x_1+w_2x_2+b z=w1x1+w2x2+b拟合真实值,最后 z z z会被代入到激活函数中(如Relu、Sigmoid等)得到:
a = σ ( z ) a=\sigma(z) a=σ(z)
再利用激活后的值 σ \sigma σ得与真实值的误差,也就是我们常说的损失函数 L ( z ) L(z) L(z),而应用反向传播的目的就是修正 z z z中的权值 w w w,使 L ( z ) L(z) L(z)达到最小,很明显,应用高等数学的知识,我们应让 L L L对 w w w求偏导以寻找最优的 w w w使 L L L最小,即:
∂ L ∂ w = ∂ L ∂ z ∂ z ∂ w \frac{\partial \mathrm{L}}{\partial \mathrm{w}}=\frac{\partial \mathrm{L}}{\partial \mathrm{z}}\frac{\partial \mathrm{z}}{\partial \mathrm{w}} ∂w∂L=∂z∂L∂w∂z
其中, ∂ z ∂ w \frac{\partial \mathrm{z}}{\partial \mathrm{w}} ∂w∂z就是 z z z对 w w w求导,即
∂ z ∂ w 1 = x 1 ∂ z ∂ w 2 = x 2 \frac{\partial \mathrm{z}}{\partial \mathrm{w_1}}=x_1\\ \frac{\partial \mathrm{z}}{\partial \mathrm{w_2}}=x_2 ∂w1∂z=x1∂w2∂z=x2
那 ∂ L ∂ z \frac{\partial \mathrm{L}}{\partial \mathrm{z}} ∂z∂L又是多少呢?这个计算过程就是我们常说的反向传播,计算过程如下:
∂ L ∂ z = ∂ L ∂ a ∂ a ∂ z = ∂ L ∂ a σ ′ ( z ) \frac{\partial \mathrm{L}}{\partial \mathrm{z}}=\frac{\partial \mathrm{L}}{\partial \mathrm{a}}\frac{\partial \mathrm{a}}{\partial \mathrm{z}} =\frac{\partial \mathrm{L}}{\partial \mathrm{a}}\sigma^{\prime}(\mathrm{z}) ∂z∂L=∂a∂L∂z∂a=∂a∂Lσ′(z)
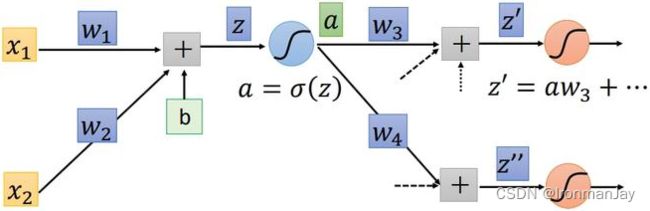
如果此时的神经网络变得稍微复杂一些,将刚才得到的 a a a,作为输入数据,结合参数 w 3 、 w 4 w_3、w_4 w3、w4等,传到另一个神经元进行同样的运算,如下图所示:
其中, ∂ a ∂ z \frac{\partial \mathrm{a}}{\partial \mathrm{z}} ∂z∂a非常容易就可以求得,为了计算 ∂ L ∂ z \frac{\partial \mathrm{L}}{\partial \mathrm{z}} ∂z∂L,需要计算 ∂ L ∂ a \frac{\partial \mathrm{L}}{\partial \mathrm{a}} ∂a∂L,此时的 ∂ L ∂ a \frac{\partial \mathrm{L}}{\partial \mathrm{a}} ∂a∂L为:
∂ L ∂ a = ∂ L ∂ z ′ ∂ z ′ ∂ a + ∂ L ∂ z ′ ′ ∂ z ′ ′ ∂ a = w 3 ∂ L ∂ z ′ + w 4 ∂ L ∂ z ′ ′ \frac{\partial \mathrm{L}}{\partial \mathrm{a}}=\frac{\partial \mathrm{L}}{\partial \mathrm{z}^{\prime}}\frac{\partial \mathrm{z}^{\prime}}{\partial \mathrm{a}} +\frac{\partial \mathrm{L}}{\partial \mathrm{z}^{\prime \prime}}\frac{\partial \mathrm{z}^{\prime \prime}}{\partial \mathrm{a}} =\mathrm{w}_{3} \frac{\partial \mathrm{L}}{\partial \mathrm{z}^{\prime}}+\mathrm{w}_{4} \frac{\partial \mathrm{L}}{\partial \mathrm{z}^{\prime \prime}} ∂a∂L=∂z′∂L∂a∂z′+∂z′′∂L∂a∂z′′=w3∂z′∂L+w4∂z′′∂L
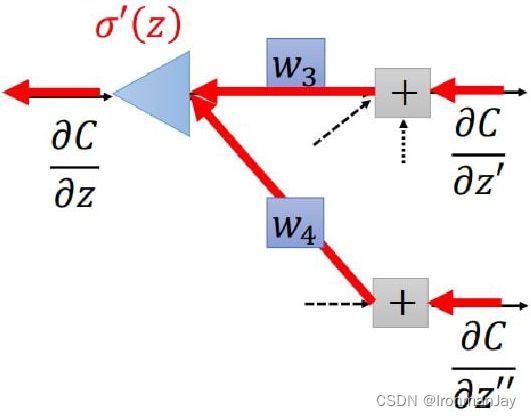
将求得的 ∂ L ∂ a \frac{\partial \mathrm{L}}{\partial \mathrm{a}} ∂a∂L代入 ∂ L ∂ z = ∂ L ∂ a ∂ a ∂ z = ∂ L ∂ a σ ′ ( z ) \frac{\partial \mathrm{L}}{\partial \mathrm{z}}=\frac{\partial \mathrm{L}}{\partial \mathrm{a}}\frac{\partial \mathrm{a}}{\partial \mathrm{z}} =\frac{\partial \mathrm{L}}{\partial \mathrm{a}}\sigma^{\prime}(\mathrm{z}) ∂z∂L=∂a∂L∂z∂a=∂a∂Lσ′(z)中,得到:
∂ L ∂ z = σ ′ ( z ) [ w 3 ∂ L ∂ z ′ + w 4 ∂ L ∂ z ′ ′ ] \frac{\partial \mathrm{L}}{\partial \mathrm{z}}=\mathrm{\sigma}^{\prime}(\mathrm{z})\left[\mathrm{w}_{3} \frac{\partial \mathrm{L}}{\partial \mathrm{z}^{\prime}}+\mathrm{w}_{4} \frac{\partial \mathrm{L}}{\partial \mathrm{z}^{\prime \prime}}\right] ∂z∂L=σ′(z)[w3∂z′∂L+w4∂z′′∂L]
这样就可以得到关于 w i ( 1 ≤ i ≤ 4 ) w_i(1≤i≤4) wi(1≤i≤4)的梯度,再应用之前讲过的随机梯度下降算法,得到最优参数。整个过程如下图所示:
因为整体是从后向前计算,所以此算法又被称为反向传播算法。
-
更新参数
利用之前定义的随机梯度下降优化器,并结合反向传播得到的参数与学习率更新参数,可以更好的拟合数据,使损失值更小
-
保存模型
将模型保存为字典形式,随着测试轮数的增加,模型的准确率会越来越高,后续就可以直接使用训练好的模型进行预测
-
保存优化器
有时候我们还需要优化器的相关内容,所以也将优化器以字典形式保存
-
打印损失
为了可视化模型的训练准确率,我们还需要打印模型的损失值,随着训练轮数的增加,模型的损失值会越来越低,而准确率会越来越高
八、加载模型
训练完模型后,就要准备测试模型的分类准确性了,所以每次在测试模型之前,都要将之前训练好的模型加载好,以便测试。注意加载的模型就是之前训练保存的模型,名字和位置不要打错。
# 加载模型
if os.path.exists('./model/model.pkl'):
model.load_state_dict(torch.load("./model/model.pkl")) # 加载保存模型的参数
九、模型测试
当我们训练并加载好模型后,就可以进行模型的测试了,这部分比较简单,就是取出数据,进行预测,然后计算准确率。
# 模型测试
def test():
correct = 0 # 正确预测的个数
total = 0 # 总数
with torch.no_grad(): # 测试不用计算梯度
for data in test_loader:
input,target = data
output=model(input) # output输出10个预测取值,其中最大的即为预测的数
probability,predict=torch.max(output.data,dim=1) # 返回一个元组,第一个为最大概率值,第二个为最大概率值的下标
total += target.size(0) # target是形状为(batch_size,1)的矩阵,使用size(0)取出该批的大小
correct += (predict == target).sum().item() # predict和target均为(batch_size,1)的矩阵,sum()求出相等的个数
print("准确率为:%.2f" % (correct / total))
虽然这部分较简单,但是仍有一些需要注意的细节,具体的步骤如下:
-
取消梯度计算
因为梯度计算是为了在训练的时候最优化参数的,而测试的时候,我们是利用训练的模型进行预测,所以不需要最优化参数,也就不需要进行梯度计算。在Pytorch中使用
torch.no_grad()取消梯度计算 -
读取测试数据
直接使用
for循环从测试数据中读取数据,分别包括:- 原始图片
- 对应的target,即真实值标签
-
预测分类
直接使用之前训练好的模型进行预测,取出概率值最大的元组,其中分别包括:
- 最大概率值
- 最大概率值的下标
这个下标就对应0~9个数字,哪个位置概率值最大,就说明分类的结果就是对应的数字
-
计算准确率
分别求出此批次的总数以及预测成功的个数,用预测成功的个数除以此批次的总数就是本批次预测的准确率,计算后打印即可
做好以上准备工作后,我们就可以在主函数中进行手写数字的识别,代码如下:
# 主函数
if __name__ == '__main__':
# 训练与测试
for i in range(5): # 训练和测试进行五轮
train()
test()
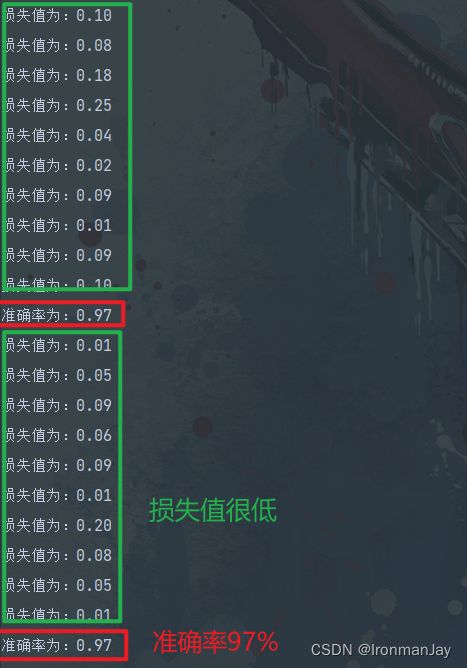
训练和测试的轮数可以自己指定,我设置为五轮,每轮首先进行模型的训练,然后使用此轮训练好的模型计算其准确率,随着训练与测试轮数的增加,模型的准确率也会逐步升高并趋于稳定。最后我们可以执行主函数来进行模型的多轮训练与预测。下图是我训练与测试的结果,可以看到模型的损失率只有 1 % 1\% 1%,而模型的准确率高达 97 % 97\% 97%,这证明我们的模型效果不错。
最终我们也将训练好的模型保存到项目中了,这也方面日后的模型测试使用,使用的时候直接调用即可。
十、自定义手写数字识别测试
如果想自己手写一个数字,看训练好的模型能否识别该怎么办呢?首先我们需要自己手写一个数字。这里有一个坑,因为训练数据都是黑底白字,所以自定义手写数字图片也应该是黑底白字,如果时白底黑字会识别出错,当然还要注意图片尺寸,应该是28*28。最后将自定义手写数字图片保存到项目中即可。
剩下的步骤就和模型测试差不多了,只是需要读取我们自己手写的图片,也是Python基础语法,细节可以看代码,剩下的部分就和模型测试没区别了,最后打印一下预测值以及自定义手写图片即可。
def test_mydata():
image = Image.open('./test/test_one.png') # 读取自定义手写图片
image = image.resize((28,28)) # 裁剪尺寸为28*28
image = image.convert('L') # 转换为灰度图像
transform = transforms.ToTensor()
image = transform(image)
image = image.resize(1,1,28,28)
output = model(image)
probability,predict=torch.max(output.data,dim=1)
print("此手写图片值为:%d,其最大概率为:%.2f" % (predict[0],probability))
plt.title('此手写图片值为:{}'.format((int(predict))),fontname="SimHei")
plt.imshow(image.squeeze())
plt.show()
最后在主函数中调用自定义测试函数即可,因为使用的是训练好的模型,所以就不需要再训练了。
# 主函数
if __name__ == '__main__':
# 自定义测试
test_mydata()
当我们运行主函数后,运行结果如下图所示,分别打印了模型预测值以及预测值的最大概率,还将读取的图片展示出来了,具体细节可见下图:
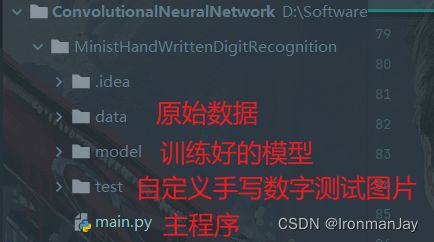
十一、项目结构图
本项目结构较简单,并没有什么不好理解的地方,为了方便读者对照查看项目,特将项目结构图列于如下,其中主要包括:
- 原始数据
- 训练好的模型
- 自定义手写数字测试图片
- 主程序
十二、全部代码
整体代码量不大,也都比较简单,为了方便读者使用于对照,特将全部代码展示如下:
import matplotlib.pyplot as plt
import torch
from torchvision.datasets import MNIST
from torchvision import transforms
from torch.utils.data import DataLoader
from torch import nn
import os
from PIL import Image
import numpy as np
# 预处理:将两个步骤整合在一起
transform = transforms.Compose({
transforms.ToTensor(), # 转为Tensor,范围改为0-1
transforms.Normalize((0.1307,),(0.3081)) # 数据归一化,即均值为0,标准差为1
})
# 训练数据集
train_data = MNIST(root='./data',train=True,download=False,transform=transforms.ToTensor())
train_loader = DataLoader(train_data,shuffle=True,batch_size=64)
# 测试数据集
test_data = MNIST(root='./data',train=False,download=False,transform=transforms.ToTensor())
test_loader = DataLoader(test_data,shuffle=False,batch_size=64)
# 模型
class Model(nn.Module):
def __init__(self):
super(Model,self).__init__()
self.linear1 = nn.Linear(784,256)
self.linear2 = nn.Linear(256,64)
self.linear3 = nn.Linear(64,10) # 10个手写数字对应的10个输出
def forward(self,x):
x = x.view(-1,784) # 变形
x = torch.relu(self.linear1(x))
x = torch.relu(self.linear2(x))
x = torch.relu(self.linear3(x))
return x
# CrossEntropyLoss
model = Model()
criterion = nn.CrossEntropyLoss() # 交叉熵损失,相当于Softmax+Log+NllLoss
optimizer = torch.optim.SGD(model.parameters(),0.8) # 第一个参数是初始化参数值,第二个参数是学习率
# 模型训练
def train():
for index,data in enumerate(train_loader):
input,target = data # input为输入数据,target为标签
optimizer.zero_grad() # 梯度清零
y_predict = model(input) # 模型预测
loss = criterion(y_predict,target) # 计算损失
loss.backward() # 反向传播
optimizer.step() # 更新参数
if index % 100 == 0: # 每一百次保存一次模型,打印损失
torch.save(model.state_dict(),"./model/model.pkl") # 保存模型
torch.save(optimizer.state_dict(),"./model/optimizer.pkl")
print("损失值为:%.2f" % loss.item())
# 加载模型
if os.path.exists('./model/model.pkl'):
model.load_state_dict(torch.load("./model/model.pkl")) # 加载保存模型的参数
# 模型测试
def test():
correct = 0 # 正确预测的个数
total = 0 # 总数
with torch.no_grad(): # 测试不用计算梯度
for data in test_loader:
input,target = data
output=model(input) # output输出10个预测取值,其中最大的即为预测的数
probability,predict=torch.max(output.data,dim=1) # 返回一个元组,第一个为最大概率值,第二个为最大值的下标
total += target.size(0) # target是形状为(batch_size,1)的矩阵,使用size(0)取出该批的大小
correct += (predict == target).sum().item() # predict和target均为(batch_size,1)的矩阵,sum()求出相等的个数
print("准确率为:%.2f" % (correct / total))
# 自定义手写数字识别测试
def test_mydata():
image = Image.open('./test/test_one.png') # 读取自定义手写图片
image = image.resize((28,28)) # 裁剪尺寸为28*28
image = image.convert('L') # 转换为灰度图像
transform = transforms.ToTensor()
image = transform(image)
image = image.resize(1,1,28,28)
output = model(image)
probability,predict=torch.max(output.data,dim=1)
print("此手写图片值为:%d,其最大概率为:%.2f" % (predict[0],probability))
plt.title('此手写图片值为:{}'.format((int(predict))),fontname="SimHei")
plt.imshow(image.squeeze())
plt.show()
# 主函数
if __name__ == '__main__':
# 自定义测试
test_mydata()
# 训练与测试
# for i in range(5): # 训练和测试进行两轮
# train()
# test()
总结
以上就是本篇博客的全部内容了,可以看到,虽然项目比较简单,是一个关于CNN的入门项目,但是要明白其中的原理却仍有一些难度,学习一样东西,我们不仅要知其然,还要知其所以然,故本篇博文从各个方面剖析了关于CNN在本项目中的应用原理。洋洋洒洒写了将近2万字,还希望对读者有帮助,那么本篇博客就到此为止了,后续还会有更多关于此方面的博客,敬请期待!