【经典问题：HanoiTower（汉诺塔）】
HanoiTower
- HanoiTower问题描述
- 模拟推导
- 问题的两种形式
-
- 求解移动总次数
- 打印详细的移动过程
HanoiTower问题描述
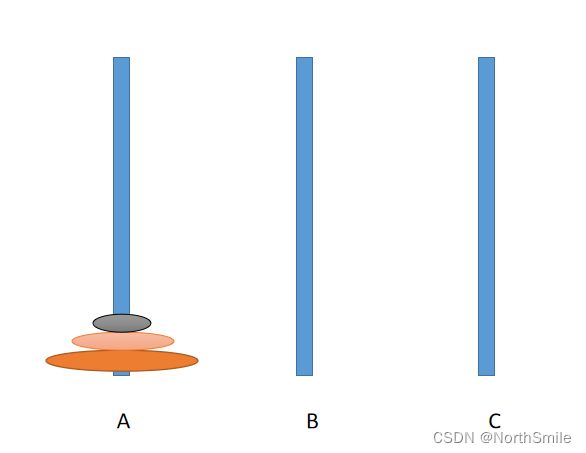
汉诺塔问题：给定A，B，C三根柱子，A为源柱，C为目标柱，B作为中转站起辅助作用，在一开始A柱上放置了N个盘子，这N个盘子自顶向下尺寸由小到大，我们的目的是，将A柱上的所有盘子均移动到C柱上，且C柱上最后盘子呈现的放置效果和A中一样。在整个移动的过程中，对于移动操作有两个限制：1）每次只能移动一个盘子；2）盘子叠放时，必须小的在上，大的在下。
这里给出一个N=3时的汉诺塔示意图：
我们的目的就是将A中的三个盘子都移动到C中，最后呈现出入下所示的效果：
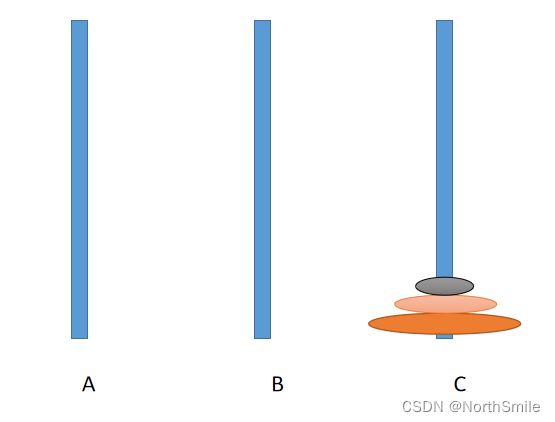
这里面B柱的作用很重要，你可以想一下：给你一瓶康师傅红茶A和一瓶康师傅绿茶C，我现在让你把红茶装在绿茶瓶子C里，而绿茶装在红茶瓶子A里，你要怎么做？是不是需要先把红茶倒在一个空瓶B中，然后将绿茶倒到现在已经空的红茶瓶子A中，最后将B瓶中的红茶装到空的绿茶瓶子C中，就完成了交换工作呢，这里B就是辅助完成交换工作的角色。
模拟推导
这里分别以N=1,2，3三种基础汉诺塔为例，进行移动的模拟过程，需要提前说明我们将A中所有盘子自顶向下编号为①，②,…：
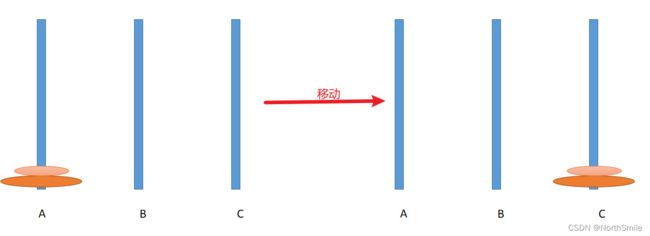
1）N=1，此时A中只有一个盘子①，此时只需要一步操作（1），①：A->C即可完成整个移动过程；
2）N=2，此时A中有两个盘子，且自顶向下，根据盘子尺寸编号为①，②，此时移动过程如下：
- （1）①：A->B，；
- （2）②：A->C，完成最大盘②的移动工作；
- （3）①：B->C，完成①盘的移动过程，也就是完成了完整的移动过程；
3）N=3，此时A中有三个盘子，且自顶向下，根据盘子尺寸编号为①，②，③此时移动过程如下：
- （1）①：A->C，；
- （2）②：A->B，C柱作为辅助；
- （3）①：C->B，C柱作为辅助，此时①②盘均在B柱中；
- （4）③：A->C，此时最大的盘子③已经移动到目标柱C中了；
- （5）①：B->A，A柱作为辅助；
- （6）②：B->C，完成②盘的移动工作；
- （7）①：A->C，A柱作为辅助，完成①盘的移动工作，也完成了整个移动过程；
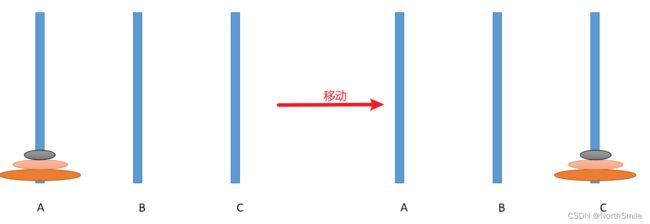
到这里应该对这个问题有了一个明显的体会了，至少已经知道如何去移动这些盘子了，那么由此会引出一些问题，比如给定盘子数量N，那么至少需要多少步操作可以完成A到C的迁移工作呢，等等。
问题的两种形式
最常见的两种相关问题形式如下，一个是求最少移动次数，另一个是打印出具体的移动过程，我们分别来看一下这些问题：
求解移动总次数
我记得我第一次碰到这个问题应该是高中数学学习数学归纳法那里吧。这个问题比较简单，只需要分别模拟N=1,2，3时的移动过程，找到盘子数量与移动次数之间的关系表达式即可求解该问题。
那么来看一下，上一节我已经完整描述了他们各自的移动过程，有以下结论：
| 盘子数量N | 移动次数hanoi(N) |
|---|---|
| N=1 | hanoi(1)=1 |
| N=2 | hanoi(2)=3 |
| N=3 | hanoi(1)=7 |
大家有没有发现什么规律呢？我用公式来描述这个规律如下：
也就是说除了只有一个盘子这种特殊情况以外，其他情况时N个盘子对应的移动次数都和N-1盘子对应的情况有关，这显然是一个递归调用过程：
给出Java代码：
public int hanoi(int n) {
// 特殊情况：n=1
if (n==1){
return 1;
}
// 其他情况：
return 2*hanoi(n-1)+1;
}
打印详细的移动过程
上面的问题只能得到移动次数，但是具体怎么移动的我们并不清楚，而汉诺塔相关的另一问题就是，打印出具体详细的移动过程，类似如下信息：
给出Java代码：
还是递归的思想，递归的核心是什么？我们要知道我们定义的这个递归函数的语义：这个函数是用来干什么的，它的输入是什么，它能实现什么功能呢？这是写出一个递归函数所要掌握的能力。
比如这里递归函数是hanoi(int n,char A,char B,char C)，那么A表示源地址，C表示目标地址，B作为辅助的中转站存在，我通过这个函数可以将源A中的所有盘子移动到目的C中。而整个移动过程可以分为以下三大步：
- 将A中最大盘上面的n-1个盘子全部移动到B中，暂时存放，此时C起到辅助的作用；
- 将最大盘n直接移动到目的位置C中；
- 将B中的n-1个盘子移动到C中，完成整个移动过程，在此期间A作为辅助出现，防止移动操作违背移动规则；
public int steps=0; // 记录移动次数
/**
* 将源柱A中的n个盘子移动到目标柱C中，B柱作为辅助
* @param n 盘子数量
* @param A 源柱
* @param B 辅助
* @param C 目标柱
*/
public void hanoi(int n,char A,char B,char C) {
// 特殊情况，一步操作
if (n==1){
steps++;
printMovePath(1,A,C);
return;
}
// 将A上的n-1个盘子移动到B中，C作为辅助
hanoi(n-1,A,C,B);
// 将A中的第n个盘子直接移动到C中
steps++;
printMovePath(n,A,C);
// 将B上的n-1个盘子移动到C中，A作为辅助
hanoi(n-1,B,A,C);
}
// 将目标src中的编号为n的盘子移动到dst中
public void printMovePath(int n, char src, char dst) {
System.out.printf("第%d次移动，移动盘子%d：%c->%c\n",steps,n,src,dst);
}
n=3时的移动过程如图所示：
