【RE-GCN_2021.04】基于进化表示学习的时态知识图谱推理

提示：

---

摘要

Knowledge Graph (KG) reasoning that predicts missing facts for incomplete KGs has been widely explored. However, reasoning over Temporal KG (TKG) that predicts facts in the future is still far from resolved. The key to predict future facts is to thoroughly understand the historical facts. A TKG is actually a sequence of KGs corresponding to different timestamps, where all concurrent facts in each KG exhibit structural dependencies and temporally adjacent facts carry informative sequential patterns. To capture these properties effectively and efficiently, we propose a novel Recurrent Evolution network based on Graph Convolution Network (GCN), called RE-GCN, which learns the evolutional representations of entities and relations at each timestamp by modeling the KG sequence recurrently. Specifically, for the evolution unit, a relation-aware GCN is leveraged to capture the structural dependencies within the KG at each timestamp. In order to capture the sequential patterns of all facts in parallel, the historical KG sequence is modeled auto-regressively by the gate recurrent components. Moreover, the static properties of entities such as entity types, are also incorporated via a static graph constraint component to obtain better entity representations. Fact prediction at future timestamps can then be realized based on the evolutional entity and relation representations. Extensive experiments demonstrate that the RE-GCN model obtains substantial performance and efficiency improvement for the temporal reasoning tasks on six benchmark datasets. Especially, it achieves up to 11.46% improvement in MRR for entity prediction with up to 82 times speedup comparing to the state-of-the-artbaseline.
  预测不完整 KG 缺失事实的知识图谱推理已得到广泛探索。然而，预测未来事实的 Temporal KG (TKG) 推理仍远未解决。预测未来事实的关键是要透彻了解历史事实。 TKG 实际上是对应于不同时间戳的一系列 KG，其中每个 KG 中的所有并发事实都表现出结构依赖性，并且时间上相邻的事实携带信息序列模式。为了有效且高效地捕获这些属性，我们提出了一种基于图形卷积网络 (GCN) 的新型循环进化网络，称为 RE-GCN，它通过对 KG 序列进行循环建模来学习每个时间戳的实体和关系的进化表示。具体来说，对于进化单元，利用关系感知 GCN 在每个时间戳捕获知识图谱内的结构依赖性。为了并行捕获所有事实的顺序模式，历史 KG 序列由门循环组件自动回归建模。此外，实体的静态属性（如实体类型）也通过静态图约束组件合并，以获得更好的实体表示。然后可以基于进化实体和关系表示来实现未来时间戳的事实预测。大量实验表明，RE-GCN 模型在六个基准数据集上的时间推理任务中获得了实质性的性能和效率提升。特别是，与最先进的基线相比，实体预测的 MRR 提高了 11.46%，加速高达 82 倍。

CCS CONCEPTS CCS概念
Computing methodologies Temporal reasoning. 计算方法 时序推理

---

关键词
时态知识图谱、演化表示学习、图卷积网络

ACM Reference Format:
Zixuan Li1,2, Xiaolong Jin1,2, Wei Li3, Saiping Guan1,2, Jiafeng Guo1,2, HuaweiShen1,2, Yuanzhuo Wang1,2and Xueqi Cheng1,2. 2018. Temporal Knowl-edge Graph Reasoning Based on Evolutional Representation Learning. InWoodstock ’18: ACM Symposium on Neural Gaze Detection, June 03–05, 2018,Woodstock, NY . ACM, New York, NY, USA, 10 pages. https://doi.org/10.1145/1122445.1122456

一、引言

  知识图谱 (KGs) 促进了许多现实世界的应用 [44]。然而，它们通常是不完整的，这限制了基于 KG 的应用程序的性能和范围。为了缓解这个问题，对试图预测缺失事实的 KG [2, 35] 进行推理是自然语言处理中的一项关键任务。传统上，知识图谱被认为是静态的多关系数据。然而，最近大量基于事件的交互数据 [3] 表现出复杂的时间动态，这就产生了对可以在时间知识图 (TKG) [3、11、12] 上进行表征和推理的方法的需求。 TKG 中的事实可以用（主体实体、关系、客体实体、时间戳）的形式表示。实际上，一个 TKG 可以表示为带有时间戳的 KG 序列，每个 KG 都包含在同一时间戳同时出现的事实。图 1 的左侧部分说明了来自 ICEWS18 [16] 数据集的 TKG 示例。尽管 TKG 无处不在，但对此类数据进行推理的方法在有效性和效率方面都相对缺乏探索。

从时间戳 $t_0到t_T$主要对 TKG 的推理有两个设置，插值和外推 [16]。前者[4，9，21]试图推断从$t_0到t_T$[16]的缺失事实。后者[16，17，33，34]旨在预测时间$t>t_T$的未来事实（事件），更具挑战性。对于TKG来说，根据观察到的历史KG预测未来时间戳的新事实有助于理解事件的隐藏因素和对新出现的事件做出反应[20，25，26]。因此，外推设置下的推理非常重要，并且对许多实际应用都有帮助，例如救灾[31]和财务分析[1]。在本文中，时间推理任务（即在 TKG 上的外推设置下的推理）包含两个子任务，如图 1 右侧所示：

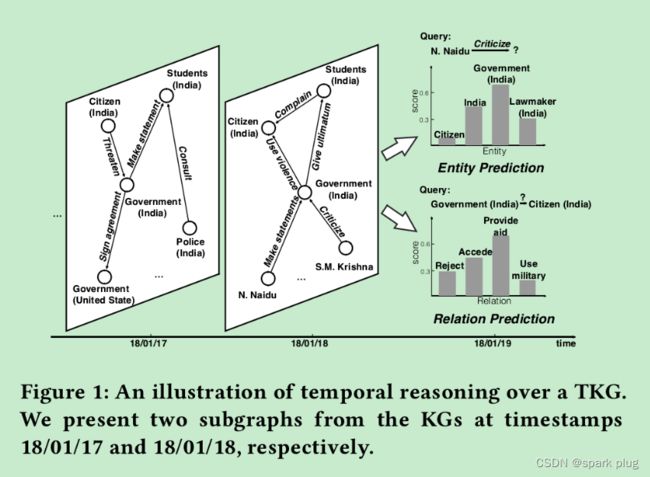
图1：TKG上时间推理的示意图。我们给出了KGs在时间戳18 / 01 / 17和18 / 01 / 18处的两个子图。

• **实体预测：**预测哪个实体在未来的某个时间戳下将与给定实体一起具有给定的关系(e.g., Who will N.Naidu criticize at 18/01/19?);
• 关系预测： 预测两个给定实体在未来某个时间戳下将发生的关系（例如，在 18/01/19 时，政府（印度）和公民（印度）之间会发生什么？）

  为了准确预测未来事实，它要求模型深入研究历史事实。在每个时间戳处，实体通过并发事实相互影响，这些事实形成KG并表现出复杂的结构依赖关系。如图1所示，18年1月18日的并发事实表明，政府（印度）受到许多人的压力，这可能会影响政府（印度）在19年1月18日的行为。此外，体现在时间相邻事实中的每个实体的行为可能带有信息性的顺序模式。如图1所示，奈杜的历史行为反映了他的偏好，并在一定程度上影响了他未来的行为。这两种历史信息的结合，驱动了实体和关系的行为趋势和偏好。

  一些早期的尝试包括 Know-evolve [33] 及其扩展 Dy Rep [34]，通过将历史中所有事实的发生建模为时间点过程来学习进化实体表示。但是，它们无法在相同的时间戳中对并发事实进行建模。最近的一些尝试以启发式的方式为每个单独的查询提取一些相关的历史信息。具体来说，RE-NET [16, 17] 在实体预测的每个查询中提取给定实体的那些直接参与的历史事实，然后对其进行顺序编码。 Cy GNet [43] 对具有相同实体和与实体预测的每个查询的关系的历史事实进行建模，因此主要侧重于预测具有重复模式的事实。由于一个TKG实际上是一个KG序列，现有的方法主要存在三个限制：（1）主要关注给定查询的实体和关系，而忽略了每个时间戳的KG中所有事实之间的结构依赖性； (2) 对每个查询单独编码历史，效率低下； (3) 忽略实体类型等实体的一些静态属性的作用。此外，现有方法仅关注实体预测，而关系预测不能由同一模型同时解决。

  在这项工作中，我们将 TKG 视为一个 KG 序列，并对整个 KG 序列统一建模，将所有历史事实编码为实体和关系表示，以促进实体和关系预测任务。因此，我们提出了一种新的基于 GCN 的循环进化网络，即 RE-GCN，它通过循环建模 KG 序列来学习每个时间戳的实体和关系的进化表示。具体来说，对于每个进化单元，利用关系感知的 GCN 在每个时间戳捕获 KG 内的结构依赖性。通过这种方式，可以有效地对 KG 中所有事实之间的交互进行建模。历史 KG 序列由门循环组件自动回归建模，以有效地捕获所有时间相邻事实的顺序模式。 TKG 中实体和关系的所有历史信息都是并行编码的。此外，实体的静态属性，如实体类型，也通过静态图约束组件被合并以获得更好的实体表示。然后，可以基于进化表示实现未来时间戳的实体预测和关系预测任务。
  总的来说，本文做出了以下贡献：

• 我们提出了一种进化表示学习模型RE-GCN，用于TKGs的时间推理，该模型考虑了KG中并发事实之间的结构依赖性，跨时间相邻事实的顺序模式以及实体的静态属性。据我们所知，这是第一项将它们全部整合到时间推理的进化表征中的研究。
• 通过从KG序列的角度表征TKG，RE-GCN有效地将TKG中的所有历史信息建模为进化表示，这些表示同时适用于实体和关系预测。因此，与最先进的基线相比，它可以实现高达 82 倍的加速。
• 大量实验表明，通过更全面地对历史进行建模，RE-GCN在六个常用基准上实现了实体和关系预测任务的一致且显着更好的性能（MRR提高了11.46%）。

二、相关工作

静态知识图谱推理 现有的静态KG推理模型试图推断KG中缺失的事实。 最近，基于嵌入的模型[2，6，30，35，41]引起了很多关注。由于GCN [19]是将内容和结构特征组合在图中的代表性模型，一些研究将其推广到关系感知GCN以处理KG。其中，R-GCN [28] 使用特定于关系的过滤器扩展了 GCN，WGCN [30] 在聚合过程中利用了可学习的关系特定权重。VR-GCN [42] 和 CompGCN [36] 在 GCN 聚合期间将节点和关系联合嵌入到关系图中。以上模型都是在静态KG中设置的，无法预测未来的事实。

时序知识图谱推理 TKG的推理可分为插值和外推两种设置[16]。对于第一个设置，模型 [4， 8–10， 13， 21， 27， 37， 38， 40] 尝试推断历史时间戳处缺失的事实。TA-DistMult [9]、TA-Trans E [9] 和 TTrans E [21] 将事实发生的时间整合到关系的嵌入中。HyTE [4] 将每个时间戳与相应的超平面相关联。但是，它们无法预测未来时间戳的事实，并且不能直接与外推设置兼容。

图 2：用于时间戳 t + 1 的时间推理的拟议 RE-GCN 模型的说明性图。

表 1：重要符号及其说明。

notations	Descriptions
$G,G^S,G_t$	TKG,静态图，在TKG中在时间戳$t$的KG
$V,R,E_t$	TKG 中的实体集、关系集、事实集（在 t 处）
$V^S,R^S,E^S$	静态图中的实体集、关系集、边缘集
$H_t,R_t$	嵌入实体矩阵，在 t 处的关系
$H,R$	实体和关系的随机初始化嵌入矩阵
$H^S$	静态图中实体的静态嵌入矩阵

  本文重点关注的外推设置试图根据历史数据预测未来时间戳的新事实。与我们的工作正交，一些模型 [14、33、34] 通过时间点过程估计条件概率来进行未来事实预测。他们更有能力对具有连续时间的 TKG 进行建模，在这种情况下，同一时间戳可能不会出现任何事实。 Glean [5] 将事件摘要构建的词图纳入未来事实预测的建模中。然而，在实际应用中并不是所有的事件都有摘要文本。 CyGNet [43] 和 RE-NET [16] 是与我们最相关的作品。他们试图从每个给定查询的角度解决实体预测任务，该查询将与每个查询中的主题实体相关的历史事实编码。 CyGNet 使用生成复制网络来模拟具有相同主题实体的历史事实的频率以及与给定查询的关系（即重复模式）。 RE-NET 使用 GCN 和 GRU 对与给定主题实体相关的 1-hop 子图序列进行建模。他们都忽略了不同时间戳的知识图谱内部的结构依赖性和实体的静态属性。不同的是，RE-GCN 将 KG 序列建模为一个整体，它考虑了所有的结构依赖性，并且能够极大地提高效率。

三、问题表述

  A TKG G 可以形式化为具有时间戳的 KG 序列，即 $G=\{G1，G2，...，Gt，...\}$。每个KG，$G_t=（V，R，E_t），$时间戳$t$是一个有向多关系图，其中$V$是实体集，$R$是关系集，$E_t$是时间戳$t$处的事实集（$t$是离散整数）。$E_t$ 中的任何事实都可以表示为四重 $（s，r，o，t）$，其中 $s，o\in V$和 $r\in R$。它表示关系 $r$ 的事实，该事实以 $s$ 作为其主主体，$o$ 作为其对象实体，在时间戳 $t$ 处发生。对于每个四元组$（s，r，o，t）$，逆四元组$（o，r^{-1}，s，t）$也会附加到数据集中。静态图表示为 $G^s=（V^s，R^s，E^s）$，其中 Vs、Rs 和 E s 是静态图中的实体集、关系集和边集。重要的数学符号如表1所示。
  实体预测任务旨在预测查询的缺失对象实体$（s、r、？、t+1）$和查询的缺失主体实体$（？、r、o、t+1）$。关系预测任务尝试预测查询的缺失关系$（s，？，o，t+1）$。假设未来时间戳$t+1$ 的事实预测取决于最近 $m$个时间戳$（即\{Gt-m+1，...Gt\}）$，并在实体 $H_t\in {\mathbb{R}}^{|V|\times d}$和关系 $R_t\in {\mathbb{R}}^{|R|\times d}$时间戳 $t$ 处的进化嵌入矩阵中建模历史 KG 序列的信息（$d$ 是嵌入的维度），两个时间推理任务的问题可以表述如下：

  问题 1.实体预测。给定一个查询 $（s，r，？，t+1）$，RE-GCN 用主体实体 s、关系 r 和给出的历史 KG 序列 $G_{t-m+1:t}$对所有对象实体的条件概率向量进行建模：
$$p(o|s,r,G_{t-m+1:t})=p(o|s,r,H_t,R_t)\text{\hspace{1em}(1)}$$
  问题 2.关系预测。给定一个查询 （s， ？， o， t + 1），RE-GCN 对与主体实体 s、对象实体 o 和历史 KG 序列 Gt−m+1：t 的所有关系的条件概率向量进行建模：
$$p(r|s,o,G_{t-m+1:t})=p(r|s,o,H_t,R_t)\text{\hspace{1em}(2)}$$

四、RE-GCN模型

RE-GCN将每个时间戳的KG中的结构依赖关系，跨时间相邻事实的信息序列模式以及实体的静态属性集成到实体和关系的进化表示中。基于学习的实体和关系表示，可以使用各种分数函数对未来时间戳进行时间推理。因此，REGCN包含一个演进单元和多任务评分函数，如图2所示。前者用于编码历史KG序列并获得实体和关系的进化表示。后者包含相应任务的评分函数，最终时间戳处的进化表示（即嵌入）作为输入。

4.1 进化单元

进化单元由一个关系感知 GCN、两个门循环组件和一个静态图约束组件组成。关系感知 GCN 尝试在每个时间戳捕获 KG 内的结构依赖性。两个门循环组件自动回归地模拟历史 KG 序列。具体来说，一个时间门循环组件和一个 GRU 组件在每个时间戳对应地获得实体和关系的进化表示。静态图约束组件通过在实体的静态嵌入和进化嵌入之间添加一些约束，将静态属性集成到进化嵌入中。形式上，进化单元计算从最近 时间戳的 KG 序列$（即Gt-m+1,...,Gt）$到实体嵌入矩阵序列$（即Ht-m+1,...Ht)$和一系列关系嵌入矩阵（即 $Rt-m+1,...,Rt）$。特别地，第一个时间戳的输入，包括实体嵌入矩阵$H$ 和关系嵌入矩阵$R$，是随机初始化的。

4.1.1 并发事实之间的结构依赖性

并发事实之间的结构依赖关系通过事实捕获实体之间的关联，通过共享实体捕获关系之间的关联。由于每个KG都是一个多关系图，而GCN是图结构化数据的强大模型[28，30，36，42]，因此使用ω层关系感知GCN来建模结构依赖关系。更具体地说，对于时间戳 $t$ 处的 KG，第 $l\in [0，\omega -1]$ 层的对象实体 $o$ 从消息传递框架下的主题实体获取信息，并考虑在第 $l$ 层嵌入关系，并在下一个 $l+1$ 层获得其嵌入，即
$$h_{o,t}^{l+1}=f\left(\frac{1}{c_o}\sum _{(s,r),\exists (s,r,o)\in {\epsilon }_t}{W}_1^l(hls,t+r_t)+W_2^l{h}_{o,t}^l\right),\text{\hspace{1em}(3)}$$
其中$h_{o，t}^l、h_{s、t}^l、r_t$ 分别表示实体 $o$、$s$ 和关系 $r$ 在时间戳 $t$ 处的第 $l^{th}$ 层嵌入;$W_1^l、W_2^l$ 是第$l^{th}$层中聚合特征和自循环的参数;$h_{s、t}^l+r_t$ 通过关系 $r$ 暗示主体和相应客体实体之间的平移属性;$c_o$是一个归一化常数，等于实体 $O$ 的度数;$f(\cdot )$是RReLU激活函数[39]。请注意，对于那些不涉及任何事实的实体，仅执行具有额外参数 $W_3^l$ 的自循环操作。实际上，关系感知 GCN 根据每个时间戳发生的事实获取实体嵌入，自循环操作可以视为实体的自我演化。

4.1.2 跨时间邻近事实的序列模式

对于一个实体$o$，其历史事实中包含的时序模式反映了其行为趋势和偏好。为了尽可能多地覆盖历史事实，模型需要考虑所有时间上相邻的事实。作为关系感知 GCN 最后一层的输出，$h_{o,t-1}^{\omega }$，已经在时间戳 $t-1$ 处对相邻事实的结构进行建模，这是一种包含时间相邻事实信息的直接有效的方法是使用 $t-1,H_{t-1}$ 处的输出实体嵌入矩阵，作为关系感知 GCN 在$t,H_t^0$ 处的输入。因此，潜在的顺序模式是通过堆叠 层关系感知 GCN 来建模的。然而，尽管相邻的 KG 不同，但当相同实体对在相邻时间戳处发生重复关系时，也存在过度平滑问题 [19]，即实体的嵌入收敛到相同的值 [43]。并且当历史KG序列变长时，GCN的大量堆叠层可能会导致梯度消失问题。因此，在 [23] 之后，我们应用时间门循环组件来缓解这些问题。这样，实体嵌入矩阵 H 由两部分确定，即关系感知 GCN 最后一层在时间戳$t$ 的输出 $H_t^{\omega }$ 和来自前一个时间戳的 $H_{t-1}$。正式地，
$$H_t=U_t\otimes H_t^{\omega }+(1-U_t)\otimes H_{t-1}\text{\hspace{1em}(4)}$$
其中⊗表示点积运算。时门 $U_t\in {\mathbb{R}}^{d\times d}$进行非线性变换如下：
$$U_t=\sigma (W_4{H}_{t-1}+b),\text{\hspace{1em}(5)}$$
其中$\sigma (\cdot )$ 是 sigmoid 函数，$W_4\in {\mathbb{R}}^{d\times d}$ 是时间门的权重矩阵。此外，关系的顺序模式捕获了相应事实中涉及的实体的信息。因此，关系 $r_t$ 在时间戳 $t$ 处的嵌入受 $r$ 相关实体 $V_{r，t}=i|（i，r，o，t）或（s，r，i，t）\in {\epsilon }_t$ 在时间戳 $t$ 处，在时间戳 $t-1$ 处嵌入它自己的嵌入。因此，采用GRU组件对关系的顺序模式进行建模。

通过在时间戳 t − 1、Ht−1、Vr，t 处对 r 相关实体的嵌入矩阵应用平均池化运算，关系 r 在时间戳 t 处的 GRU 输入为
$$r_t^{\prime }=[pooling(H_{t-1},v_{r,t});r],\text{\hspace{1em}(6)}$$
其中 $r$ 是关系 $r$ 在 $R$ 中的嵌入，$[;]$ 表示向量连接操作。对于没有相应事实的关系，在时间戳 $t$ 处发生，$r_t^{\prime }=0$。然后我们通过 GRU 将关系嵌入矩阵 $R_{t-1}$ 更新为 $R_t$，
$$R_t=GRU(R_{t-1},R_t^{\prime }),\text{\hspace{1em}(7)}$$
其中 $R_t^{\prime }\in {\mathbb{R}}^{|R|\times d}$ 由所有关系的 $r_t^{\prime }$ 组成。请注意，$H_t和R_t$ 每行的 $L_2$ 范数被限制为 1。

4.1.3 静态特性

除了历史 KG 序列中包含的信息外，实体的一些静态属性形成静态图，可以看作是 TKG 的背景知识，有助于模型学习更准确的实体进化表示。因此，我们将静态图合并到进化表示的建模中。我们根据最初包含在实体名称字符串中的实体属性信息，从 ICEWS 构建了三个 TKG 的静态图。其中的实体名称串大多为“实体类型（国家）”形式。以 ICEWS18 [17] 中名为“警察（澳大利亚）”的实体为例，我们将此实体的关系“isA”添加到财产实体“警察”，将关系“国家”添加到财产实体“澳大利亚”。图 2 的左下方显示了一个静态图的示例。由于静态图是一个多关系图，R-GCN [28] 可以对多关系图进行建模，而无需任何额外的关系嵌入。因此，我们采用没有自循环的 1 层 RGCN [28] 来获得 TKG 中实体的静态嵌入。然后，静态图的更新规则定义如下：
$$hsi={\rm Y}\left(\frac{1}{ci}\sum _{(rs,j),\exists (i,rs,j))\in Es}{W}_{r^s}{h}_i^{\prime s}(j)\right),\text{\hspace{1em}(8)}$$
其中 $h_i^s和h_j^{\prime s}$ 是 $H^s$ 和 $H^{\prime s}$ 的第 $i^{th}行和第j^{th}$ 行，分别是输出和随机初始化的输入嵌入矩阵;$Wrs\in Rd\times d$ 是 R-GCN 中 $rs$ 的关系矩阵;${\rm Y}(\cdot )$ 是 ReLU 函数;$c_i$ 是一个规范化常量，等于与实体 $i$ 连接的实体数。请注意，$||H_i^S|{|}_2=1$。

反映实体嵌入矩阵 Ht−m、Ht−m+1 学习序列中的静态属性,…Ht，我们将同一实体的进化嵌入和静态嵌入之间的角度限制为不超过时间戳相关阈值。它随着时间的推移而增加，因为实体进化嵌入的允许变量范围随着时间的推移不断扩大，越来越多的事实发生。因此，它被定义为
$$\theta x=min(\gamma x,90^{◦}),\text{\hspace{1em}(9)}$$
其中$\gamma$表示角度和 $x\in [0，1，..，m]$ 的上升速度。我们将实体的两个嵌入的最大角度设置为 $90^{◦}$。
然后，实体 i 的两个嵌入之间的角度的余弦值，记为 $cos(h_i^s，h_{t-m+x,i})，应大于cos\theta x$ 。
因此，静态图约束分量在时间戳 $t$ 处的损失可以定义如下：
$$L_x^{st}=\sum _{i=0}^{|V|-1}max\{cos\theta x-cos(h_i^s，h_{t-m+x,i}),0\}.\text{\hspace{1em}(10)}$$
静态图约束组件的损失为$L^{st}={\sum }_{x=0}^m{L}_x^{st}$

4.2 针对不同任务的评分函数

以前关于KG推理的工作[6，30，36]涉及分数函数（即解码器）来模拟方程（1）和（2）中的条件概率，可以看作是候选三元组（s，r，o）的概率得分。由于之前的工作[36]表明，具有卷积得分函数的GCN在KG推理方面具有良好的性能，为了反映方程（3）中隐含的实体和关系的进化嵌入的翻译特性，我们选择ConvTransE [30]作为我们的解码器。ConvTransE 包含一个一维卷积层和一个全连接层。我们使用ConvTransE（·）来表示这两个层。然后，所有实体的概率向量如下：
$$p(o|s,r,H_t,R_t)=\sigma (H_{t}ConvTransE(s_t,r_t)).\text{\hspace{1em}(11)}$$ 同样，所有关系的概率向量如下：
$$p(r|s,o,H_t,R_t)=\sigma (R_{t}ConvTransE(s_t,o_t)).\text{\hspace{1em}(12)}$$其中$\sigma (\cdot )$是sigmoid函数，$s_t，r_t，o_t$分别是$H_t$和$R_t$中$s，r和o$的嵌入。$ConvTransE(s_t,r_t)，ConvTransE(s_t,o_t)\in {\mathbb{R}}^{d\times 1}.$为简洁起见，省略了ConvTransE的详细信息。请注意，ConvTransE 可以替换为其他评分函数。

4.3 参数学习

实体预测任务和关系预测任务都可以看作是多标签学习问题。让$y_{t+1}^e\in {\mathbb{R}}^{|V|}和y_{t+1}^r\in {\mathbb{R}}^{|R|}$分别表示时间戳 $t+1$ 处的两个任务的标签向量。向量的元素 $y_{t+1}^e\in {\mathbb{R}}^{|V|}和y_{t+1}^r\in {\mathbb{R}}^{|R|}$对于确实发生的事实，为 1，否则为 0。然后
$$L^e=\sum _{t=0}^{T-1}\sum _{(s,r,o,t+1)\in E_{t+1}}\sum _{i=0}^{|V|-1}{y}_{t+1,i}^{e}log{p}_i(o|s,r,H_t,R_t),\text{\hspace{1em}(13)}$$
$$L^r=\sum _{t=0}^{T-1}\sum _{(s,r,o,t+1)\in E_{t+1}}\sum _{i=0}^{|R|-1}{y}_{t+1,i}^{r}log{p}_i(r|s,o,H_t,R_t),\text{\hspace{1em}(13)}$$
其中$T$是训练集中的时间戳数，$y_{t+1,i}^e,y_{t+1,i}^r$是$i_{th}$个元素$y_{t+1}^e,y_{t+1}^r,pi(o|s,r,H_t,R_t)和pi(r|s,o,Ht,Rt)$是实体 i 和关系 i 的概率得分。
两个时间推理任务是在多任务学习框架下进行的。因此，最终损耗 $L={\lambda }_1{L}^e+{\lambda }_2{L}^r+L^{st}。{\lambda }_1和{\lambda }_2$ 是控制损失项的参数。

4.4 计算复杂度分析

为了了解所提出的RE-GCN的效率，我们分析了其演化单元的计算复杂性。关系感知 GCN 在时间戳 t 处的时间复杂度为 $O(|E|\omega )$，其中|E|是历史 KG 序列中并发事实的最大数量。在每个时间戳获取 GRU 组件输入的池化操作具有时间复杂度 O （|R|D），其中 D 是时间戳 t 和 | 处关系中涉及的最大实体数R |是关系集的大小。获取静态嵌入的时间复杂度为 O （|埃斯|）。当我们展开 GRU 组件和关系感知 GCN 的 m 步时，演化单元的时间复杂度最终为 $O（m（|E|\omega +|R|D）+|E^s|）$。

五、实验

5.1 实验设置

5.1.1 数据集

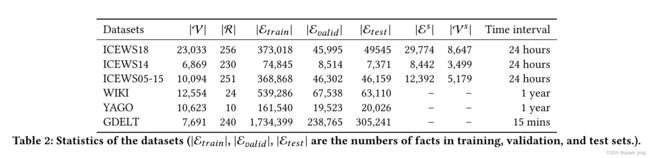
以前的作品中常用的TKG有六种，即ICEWS18 [16]，ICEWS14 [9]，ICEWS05-15 [9]，WIKI [21]，YAGO [24]和GDELT [22]。前三个数据集来自综合危机预警系统[3]（ICEWS）。GDELT [16] 来自全球事件、语言和语气数据库 [22]。我们在所有这些数据集上评估RE-GCN。我们将 ICEWS14 和 ICEWS05-15 分为训练集、验证集和测试集，比例分别为 80%、10% 和 10%，时间戳在 [16] 之后。数据集的详细信息如表2所示。时间间隔表示时间相邻事实之间的时间粒度。

5.1.2 评估指标

在实验中，MRR和$Hits@1，3，10$被用作实体预测和关系预测的指标。对于WIKI和YAGO上的实体预测任务，我们只报告MRR和Hits@3结果，因为之前的工作RE-NET没有报告Hits@1的结果[16]。

如 [7， 14， 15] 中所述，[2， 16， 43] 中使用的过滤设置（从损坏事实的排名列表中删除训练、验证或测试集中出现的所有有效事实）不适用于时间推理任务。例如，以测试集中答案为 o1 的典型查询 （s， r， ？， t1） 为例，并假设存在另一个事实 （s， r， o2， t2）。在此过滤设置下，o2 将被错误地视为正确答案，从而从候选答案的排名列表中删除。但是，o2 对于给定的查询是不正确的，因为 （s， r， o2） 发生在时间戳 t2 而不是 t1 处。因此，筛选的设置可能会获得不正确的更高排名分数。在不损失一般性的情况下，仅报告原始设置下的实验结果。

5.1.3 基线

将RE-GCN模型与两类模型进行了比较：静态KG推理模型和TKG推理模型。DistMult [41]、ComplEx [35]、R-GCN [28]、ConvE [6]、ConvTransE [30]、RotatE [32] 被选为静态模型。HyTE [4]、TTransE [21] 和 TA-DistMult [9] 被选为插值设置下的时间模型。对于外推设置下的时间模型，比较了CyGNet [43]和RE-NET [16]。对于Know-evolve和DyRep，RE-NET将它们扩展到时间推理任务，但不发布其代码。因此，我们只在他们的论文中报告结果。此外，GCRN [29] 是齐次图的模型，RE-NET 通过用 R-GCN 替换 GCN 将其扩展到 R-GCRN。

5.1.4 实施细则

对于进化单元，嵌入维度设置为200； YAGO 的关系感知 GCN 的层数 设置为 1，其他数据集设置为 2；对于关系感知 GCN 的每一层，dropout rate 设置为 0.2。我们在验证集上对历史图序列 (1, 15) 的长度和角度$\gamma (1^{◦}-20^{◦})$ 的上升速度执行网格搜索。 ICEWS18、ICEWS14、ICEWS05-15、WIKI、YAGO 和 GDELT 的最佳历史长度 分别为 6、3、10、2、1、1。 实验性地设置为 10°。采用 Adam [18] 进行参数学习，学习率为 0.001。至于静态图约束组件中使用的 RGCN，我们将块维度设置为 2×2，每层的丢失率设置为 0.2。对于 ConvTransE，内核数设置为 50，内核大小设置为 2×3，dropout 率设置为 0.2。对于实体预测任务和关系预测任务的联合学习，1 和2 在实验上分别设置为 0.7 和 0.3。静态图的统计数据如表 2 所示。我们仅在 WIKI、YAGO 和 GDELT 上报告没有静态图约束的结果，因为这些数据集中缺少静态信息。
为了在验证集和测试集中进行多步推理[16]，我们评估RE-GCN的性能，在训练集的最终时间戳处将实体和关系的进化嵌入作为[43]之后的得分函数的输入。此外，我们还报告了在测试集上进行多步推理时给出的具有真实历史的模型的结果，即 w. GT。所有实验都是在特斯拉V100上进行的。代码可在 https://github.com/Lee-zix/RE-GCN 获得。

5.2 实验结果

5.2.1 实体预测的结果

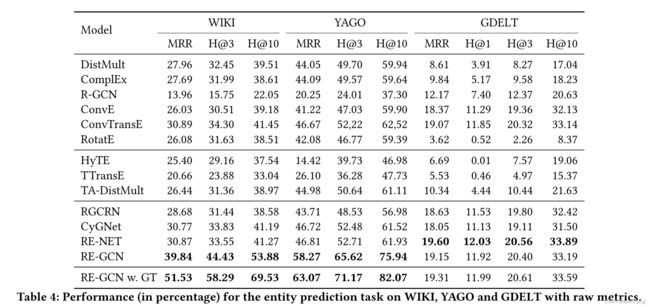
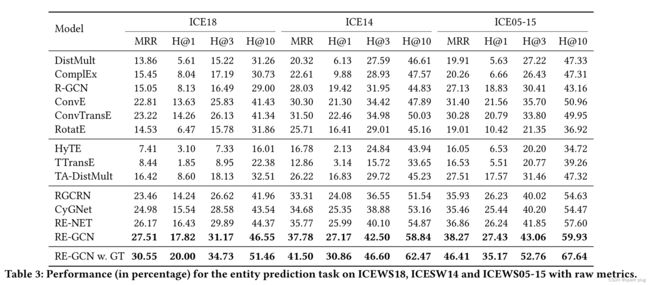
实体预测任务的实验结果如表 3 和表 4 所示。REGCN 在三个 ICEWS 数据集 WIKI 和 YAGO 上始终优于基线。结果令人信服地验证了其有效性。具体来说，RE-GCN 明显优于静态模型（即表 3 和表 4 的第一块中的模型），因为 REGCN 考虑了跨时间戳的顺序模式。 RE-GCN 比插值设置的时间模型（即表 3 和表 4 第二块中的模型）表现更好，因为 RE-GCN 还捕获了时间序列模式和实体的静态属性。因此，它可以为未观察到的时间戳获得更准确的进化表示。特别是，RE-GCN 在外推设置方面优于时间模型（即表 3 和表 4 第三块中的模型）。它优于 RGCRN，因为新设计的图卷积运算和进化单元中的两个循环组件学习了更好的进化嵌入，而静态图有助于学习更好的实体进化嵌入。 CyGNet 和 RE-NET 的良好性能验证了重复模式和 1-hop 邻居对实体预测任务的重要性。尽管如此，RE-GCN 的性能优于 CyGNet 也就不足为奇了，因为除了历史中的重复模式之外，还有很多有用的信息。 RE-GCN 的性能也优于 RE-NET，后者忽略了 KG 内的结构依赖性和实体的静态属性。通过捕获更全面的结构依赖性和顺序模式，RE-GCN 在大多数数据集上都优于 RE-NET。从表 3 和表 4 的最后两行可以看出，当数据集的两个相邻时间戳之间的时间间隔变大时，最后两行之间的性能差距变大。对于 WIKI 和 YAGO 这两个数据集，时间间隔为一年，在不知道 ground truth 历史的情况下，模型的性能迅速下降。这是因为在多步推理过程中，当时间间隔较大时，进化表示变得不准确。
请注意，与 WIKI 和 YAGO 上的最佳基线相比，RE-GCN 甚至在 MRR 中实现了 8.97/11.46% 的改进，在 Hits@3 中实现了 10.60/12.91%，在 Hits@10 中实现了 12.61/14.01% 的改进。对于这两个数据集，由于时间间隔比其他数据集大得多，所以在每个时间戳处 KG 内部有更多的结构依赖性。因此，仅对重复模式或单跳邻居建模会丢失大量结构依赖性和顺序模式。结果表明，RE-GCN 更能够对这些包含并发事实之间复杂结构依赖性的数据集进行建模。

与其他5个数据集相比，静态模型和时态模型在GDELT上的实验结果同样较差。我们进一步分析了GDELT数据集，发现其中许多实体都是抽象概念，并不表示特定的实体（例如，警察和政府）。在前50个常见实体中，28个是抽象概念，43.72%的对应事实涉及抽象概念。这些抽象的概念使得在原始环境下对某些实体进行时间推理几乎是不可能的，因为我们在不知道政府属于哪个国家的情况下无法预测它的活动。因此，所有模型只能预测 GDELT 数据集中的部分事实并获得相似的结果。此外，抽象概念产生的噪声会影响其他实体的进化表征，因为RE-GCN将KG序列建模为一个整体，这使得RE-GCN的结果比RE-NET差一点。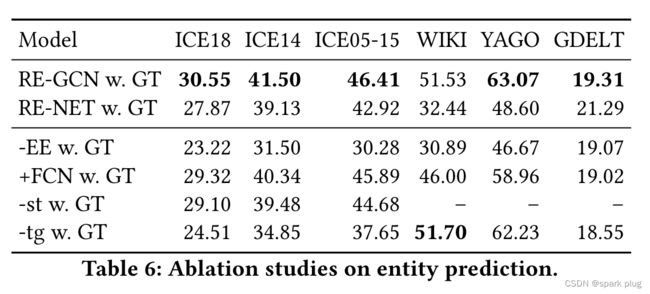

5.2.2 关系预测的结果

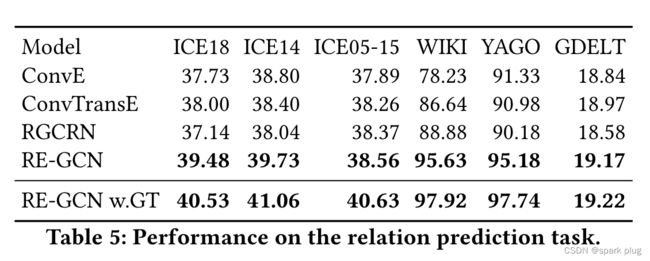
由于有些模型不是为关系预测任务和空间限制而设计的，因此我们从基线中选择典型模型，并在表5中仅根据MRR表示实验结果。更详细地说，我们从静态模型中选择了 ConvE [6]、ConvTransE [30]，以及从时态模型中选择了 RGCRN [29]。RE-NET和CyGNet没有被采用，因为它们不能直接应用于关系预测任务。可以观察到RE-GCN的性能优于所有基线。RE-GCN的优异表现表明，我们的进化单元可以通过对历史进行全面建模来获得更准确的进化表示。
RE-GCN 与其他基线在关系预测任务上的性能差距小于实体预测任务。这是因为关系的数量远远少于实体的数量。较少的候选项使关系预测任务比实体预测任务容易得多。WIKI和YAGO的性能比其他数据集好得多，因为两个数据集中的关系数量分别只有24和10。静态模型和时态模型的GDELT数据集上的结果也同样差，这再次验证了我们在5.2.1节中提到的观察结果。

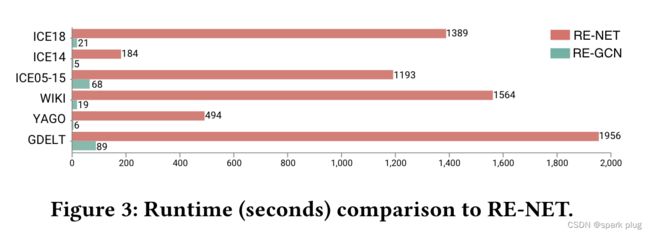
5.3 预测时间的比较

为了研究RE-GCN的效率，我们将RE-GCN与RE-NET在相同环境下对测试集进行实体预测的运行时进行了比较。为了进行公平比较，这两个模型使用给出的地面真实历史进行实体预测。从图3中的结果可以看出，RE-GCN在ICE18、ICE14、ICE0515、WIKI、YAGO和GDELT上分别比RE-NET快66、36、17、82、82、22倍。这是因为RE-NET针对每个时间戳逐个处理单个查询，而RE-GCN从KG序列的角度表征进化表示，并同时获得同一时间戳下所有查询的表示。因此，RE-GCN比最佳基线RE-NET更有效。

5.4 消融研究

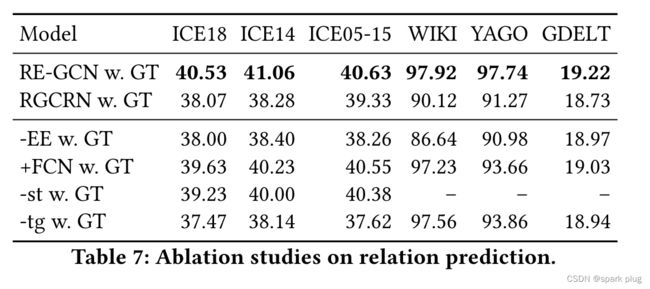
为了消除训练和测试结果测试之间的偏差，我们使用测试集上给出的地面真实历史进行所有消融研究。为了进一步显示RE-GCN每个部分的有效性，我们还在表6中报告了RE-NET w. GT的结果，在表7中报告了RGCRN w. GT的结果。

5.4.1 进化单元的影响

为了证明进化单元如何对RE-GCN的最终结果做出贡献，我们进行了仅使用ConvTransE评分函数和随机初始化的可学习嵌入的实验。结果表示为-EE w. GT，如表6和表7所示。可以看出，删除演化单元对除GDELT以外的所有数据集的结果都有很大的影响，这表明对历史信息进行建模对所有数据集都至关重要。对于GDELT，只有使用ConvTransE才能获得良好的结果。这也符合我们在 5.2.1 节中提到的观察结果。
为了进一步验证我们的演进单元在不同评分函数下的有效性，我们将RE-GCN中的ConvTransE替换为简单的单层全连接网络（FCN），表示为+FCN w. GT。实验结果如表6和表7所示。可以观察到，在大多数数据集上，结果比RE-GCN w. GT更差。它与[42]中的观察结果相符，卷积得分函数更适合GCN。然而，即使使用简单的评分函数，+FCN w. GT 在实体和关系预测方面仍然表现出色。

5.4.2 静态图形约束组件的影响

表6和表7中表示为–st w. GT的结果证明了RE-GCN在没有静态图约束分量的情况下的性能。可以看出，在ICEWS数据集中，–st w. GT的性能始终比RE-GCN w. GT差，这证明了静态图约束组件对RE-GCN模型的必要性。静态信息可以看作是TKG的背景知识。静态图中的实体类型和位置信息丰富了实体的演化表示，有助于获得更好的实体初始进化表示。请注意，即使没有静态信息，–st w. GT 的性能仍然优于最先进的 RE-NET w. GT 和 RGCRN w. GT。

5.4.3 时间门递归分量的影响

–tg w. GT 在表 6 和 7 中表示 RE-GCN 的变体，直接使用最后一个时间戳的演化表示作为当前时间戳处的演化单元的输入，没有时间门。可以观察到，与RE-GCN w. GT相比，当历史KG序列变长时，–tg w. GT的性能迅速下降，这充分表明了时门循环分量的必要性。实际上，时门循环分量有助于RE-GCN通过深度堆叠GCN捕获序列模式，当层数变大时，通常面临过度平滑和消失梯度问题。

5.5 案例研究

为了显示并发事实之间的结构依赖关系以及RE-GCN学习到的时间相邻事实的顺序模式，我们在表9中说明了REGCN给出ICEWS18测试集前1分答案的三个案例。第一种情况显示了（A，接待访问，B，t-2）可能导致（A，外交合作，B，t）的顺序模式。第二种情况表明，序列模式（A，进行轰炸，B，t-2），（B，Make statement，C，t-1）和C在时间戳t-1联合处的结构依赖关系导致了最终结果。第三种情况说明了顺序模式（A，演示，B，t-2），（B，认可，C，t-1）有助于关系预测（A，？，C，t）。通过对KG序列进行整体建模，RE-GCN不会遗漏历史记录中的有用信息。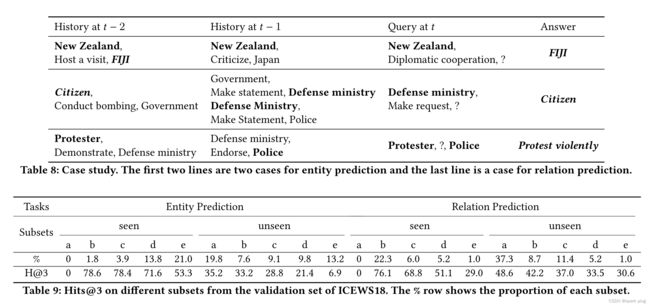

5.6 详细分析

为了深入了解RE-GCN在不同类型数据上的性能，我们对ICEWS18的验证集进行了详细的分析。对于实体预测，我们根据给定实体的单跳邻居的数量(0 (a)， 1 (b)， 2-3 ©， 4-10 (d)， >10 (e))，以及在最新的(=6)时间戳上，应答实体是否与给定实体(即，可见和不可见)有直接交互作用来拆分验证集。对于关系预测，我们根据两个给定实体(0 (a)， 1 (b)， 2-3 ©， 4-10 (d)， >10 (e))之间的关系数量，以及在最新的时间戳中是否在给定实体之间发生了答案关系，来拆分验证集。(即看得见和看不见的)。表9显示了RE-GCN的结果，每个子集上都有Hits@3。对于实体预测，可以观察到当邻居数量变大时，性能下降，而RE-GCN在两个实体在历史上见过的子集中得到更好的结果。有趣的是，RE-GCN甚至可以在主题实体没有历史的情况下进行预测。一个可能的原因是静态图和共享的初始进化表示已经提供了历史KG序列之外的一些背景知识和信息。对于关系预测，可以看出，当关系数量较大时，性能下降。表9也说明了重复事实在数据集中所占的比例，进一步证明了RE-GCN中时间门重复成分的必要性。

六、结论

本文提出了用于时间推理的RE-GCN，它通过捕获并发事实之间的结构依赖关系以及跨时间相邻事实的信息顺序模式来学习实体和关系的进化表示。此外，它将实体的静态属性（如实体类型）合并到进化表示中。因此，时间推理基于最终时间戳处的进化表示使用各种评分函数进行。六个基准的实验结果表明，RE-GCN在两个时间推理任务上具有显著的优点和优越性。通过对整个KG序列进行建模，与最先进的基线RE-NET相比，RE-GCN的实体预测速度提高了17至82倍。

七、致谢

这项工作得到了国家重点研发计划（资助2016YFB1000902）、国家自然科学基金资助U1911401、62002341、61772501、U1836206、91646120和61722211、GFKJ创新计划、北京人工智能研究院资助BAAI2019ZD0306和联想-中科院联合实验室青年科学家项目。

---

参考文献

[1] Johan Bollen, Huina Mao, and Xiaojun Zeng. 2011. Twitter mood predicts the stock market. Journal of computational science 2, 1 (2011), 1–8.
[2] Antoine Bordes, Nicolas Usunier, Alberto Garcia-Duran, Jason Weston, and Oksana Yakhnenko. 2013. Translating embeddings for modeling multi-relational data. In Advances in neural information processing systems. 2787–2795.
[3] Elizabeth Boschee, Jennifer Lautenschlager, Sean O’Brien, Steve Shellman, James Starz, and Michael Ward. 2015. ICEWS coded event data. Harvard Dataverse 12 (2015).
[4] Shib Sankar Dasgupta, Swayambhu Nath Ray, and Partha Talukdar. 2018. Hyte: Hyperplane-based temporally aware knowledge graph embedding. In Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing. 20012011.
[5] Songgaojun Deng, Huzefa Rangwala, and Yue Ning. 2020. Dynamic Knowledge Graph based Multi-Event Forecasting. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. 1585–1595.
[6] Tim Dettmers, Pasquale Minervini, Pontus Stenetorp, and Sebastian Riedel. 2018. Convolutional 2d knowledge graph embeddings. In Thirty-Second AAAI Conference on Artificial Intelligence.
[7] Zifeng Ding, Zhen Han, Yunpu Ma, and Volker Tresp. 2021. Temporal Knowledge Graph Forecasting with Neural ODE. arXiv preprint arXiv:2101.05151 (2021).
[8] Cristóbal Esteban, Volker Tresp, Yinchong Yang, Stephan Baier, and Denis Krompaß. 2016. Predicting the co-evolution of event and knowledge graphs. In 2016 19th International Conference on Information Fusion (FUSION). IEEE, 98–105.
[9] Alberto García-Durán, Sebastijan Dumančić, and Mathias Niepert. 2018. Learning sequence encoders for temporal knowledge graph completion. arXiv preprint arXiv:1809.03202 (2018).
[10] Rishab Goel, Seyed Mehran Kazemi, Marcus Brubaker, and Pascal Poupart. 2020. Diachronic embedding for temporal knowledge graph completion. In Proceedings of the AAAI Conference on Artificial Intelligence, Vol. 34. 3988–3995.
[11] Simon Gottschalk and Elena Demidova. 2018. Eventkg: A multilingual eventcentric temporal knowledge graph. In European Semantic Web Conference. Springer, 272–287.
[12] Simon Gottschalk and Elena Demidova. 2019. EventKG–the hub of event knowledge on the web–and biographical timeline generation. Semantic Web Preprint (2019), 1–32.
[13] Zhen Han, Peng Chen, Yunpu Ma, and Volker Tresp. 2020. Dyernie: Dynamic evolution of riemannian manifold embeddings for temporal knowledge graph completion. arXiv preprint arXiv:2011.03984 (2020).
[14] Zhen Han, Yunpu Ma, Yuyi Wang, Stephan Günnemann, and Volker Tresp. 2020. Graph Hawkes Neural Network for Forecasting on Temporal Knowledge Graphs. 8th Automated Knowledge Base Construction (AKBC) (2020).
[15] Prachi Jain, Sushant Rathi, Soumen Chakrabarti, et al. 2020. Temporal Knowledge Base Completion: New Algorithms and Evaluation Protocols. In Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing (EMNLP). 3733–3747.
[16] Woojeong Jin, Meng Qu, Xisen Jin, and Xiang Ren. 2020. Recurrent Event Network: Autoregressive Structure Inference over Temporal Knowledge Graphs. In EMNLP.
[17] Woojeong Jin, Changlin Zhang, Pedro Szekely, and Xiang Ren. 2019. Recurrent Event Network for Reasoning over Temporal Knowledge Graphs. arXiv preprint arXiv:1904.05530 (2019).
[18] Diederik P Kingma and Jimmy Ba. 2014. Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980 (2014).
[19] Thomas N Kipf and Max Welling. 2016. Semi-supervised classification with graph convolutional networks. arXiv preprint arXiv:1609.02907 (2016).
[20] Gizem Korkmaz, Jose Cadena, Chris J Kuhlman, Achla Marathe, Anil Vullikanti, and Naren Ramakrishnan. 2015. Combining heterogeneous data sources for civil unrest forecasting. In Proceedings of the 2015 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining 2015. 258–265.
[21] Julien Leblay and Melisachew Wudage Chekol. 2018. Deriving validity time in knowledge graph. In Companion Proceedings of the The Web Conference 2018. International World Wide Web Conferences Steering Committee, 1771–1776.
[22] Kalev Leetaru and Philip A Schrodt. 2013. Gdelt: Global data on events, location, and tone, 1979–2012. In ISA annual convention, Vol. 2. Citeseer, 1–49.
[23] Guohao Li, Matthias Muller, Ali Thabet, and Bernard Ghanem. 2019. Deepgcns: Can gcns go as deep as cnns?. In Proceedings of the IEEE International Conference on Computer Vision. 9267–9276.
[24] Farzaneh Mahdisoltani, Joanna Biega, and Fabian Suchanek. 2014. Yago3: A knowledge base from multilingual wikipedias. In 7th biennial conference on innovative data systems research. CIDR Conference.
[25] Sathappan Muthiah, Bert Huang, Jaime Arredondo, David Mares, Lise Getoor, Graham Katz, and Naren Ramakrishnan. 2015. Planned protest modeling in news and social media. In Twenty-Seventh IAAI Conference. Citeseer.
[26] Lawrence Phillips, Chase Dowling, Kyle Shaffer, Nathan Hodas, and Svitlana Volkova. 2017. Using social media to predict the future: a systematic literature review. arXiv preprint arXiv:1706.06134 (2017).
[27] Ali Sadeghian, Miguel Rodriguez, Daisy Zhe Wang, and Anthony Colas. 2016. Temporal reasoning over event knowledge graphs. In Workshop on Knowledge Base Construction, Reasoning and Mining.
[28] Michael Schlichtkrull, Thomas N Kipf, Peter Bloem, Rianne Van Den Berg, Ivan Titov, and Max Welling. 2018. Modeling relational data with graph convolutional networks. In European Semantic Web Conference. Springer, 593–607.
[29] Youngjoo Seo, Michaël Defferrard, Pierre Vandergheynst, and Xavier Bresson. 2018. Structured sequence modeling with graph convolutional recurrent networks. In International Conference on Neural Information Processing. Springer, 362–373.
[30] Chao Shang, Yun Tang, Jing Huang, Jinbo Bi, Xiaodong He, and Bowen Zhou. 2019. End-to-end structure-aware convolutional networks for knowledge base completion. In Proceedings of the AAAI Conference on Artificial Intelligence, Vol. 33. 3060–3067.
[31] Alessio Signorini, Alberto Maria Segre, and Philip M Polgreen. 2011. The use of Twitter to track levels of disease activity and public concern in the US during the influenza A H1N1 pandemic. PloS one 6, 5 (2011), e19467.
[32] Zhiqing Sun, Zhi-Hong Deng, Jian-Yun Nie, and Jian Tang. 2018. RotatE: Knowledge Graph Embedding by Relational Rotation in Complex Space. In International Conference on Learning Representations.
[33] Rakshit Trivedi, Hanjun Dai, Yichen Wang, and Le Song. 2017. Know-evolve: Deep temporal reasoning for dynamic knowledge graphs. In Proceedings of the 34th International Conference on Learning-Volume 70. JMLR. org, 3462–3471.
[34] Rakshit Trivedi, Mehrdad Farajtabar, Prasenjeet Biswal, and Hongyuan Zha. 2018. Dyrep: Learning representations over dynamic graphs. (2018).
[35] Théo Trouillon, Johannes Welbl, Sebastian Riedel, Éric Gaussier, and Guillaume Bouchard. 2016. Complex embeddings for simple link prediction. In International Conference on Machine Learning. 2071–2080.
[36] Shikhar Vashishth, Soumya Sanyal, Vikram Nitin, and Partha Talukdar. 2019. Composition-based Multi-Relational Graph Convolutional Networks. In International Conference on Learning Representations.
[37] Jiapeng Wu, Meng Cao, Jackie Chi Kit Cheung, and William L Hamilton. 2020. TeMP: Temporal Message Passing for Temporal Knowledge Graph Completion. arXiv preprint arXiv:2010.03526 (2020).
[38] Tianxing Wu, Arijit Khan, Huan Gao, and Cheng Li. 2019. Efficiently embedding dynamic knowledge graphs. arXiv preprint arXiv:1910.06708 (2019).
[39] Bing Xu, Naiyan Wang, Tianqi Chen, and Mu Li. 2015. Empirical evaluation of rectified activations in convolutional network. arXiv preprint arXiv:1505.00853 (2015).
[40] Chenjin Xu, Mojtaba Nayyeri, Fouad Alkhoury, Hamed Yazdi, and Jens Lehmann. 2020. Temporal Knowledge Graph Completion Based on Time Series Gaussian Embedding. In International Semantic Web Conference. Springer, 654–671.
[41] Bishan Yang, Wen-tau Yih, Xiaodong He, Jianfeng Gao, and Li Deng. 2014. Embedding entities and relations for learning and inference in knowledge bases. arXiv preprint arXiv:1412.6575 (2014).
[42] Rui Ye, Xin Li, Yujie Fang, Hongyu Zang, and Mingzhong Wang. 2019. A vectorized relational graph convolutional network for multi-relational network alignment. In Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence, IJCAI-19. 4135–4141.
[43] Cunchao Zhu, Muhao Chen, Changjun Fan, Guangquan Cheng, and Yan Zhan. 2020. Learning from History: Modeling Temporal Knowledge Graphs with Sequential Copy-Generation Networks. arXiv preprint arXiv:2012.08492 (2020).
[44] Xiaohan Zou. 2020. A survey on application of knowledge graph. In Journal of Physics: Conference Series, Vol. 1487. IOP Publishing, 012016.