数学建模-模拟退火算法-函数寻优（优化模型）

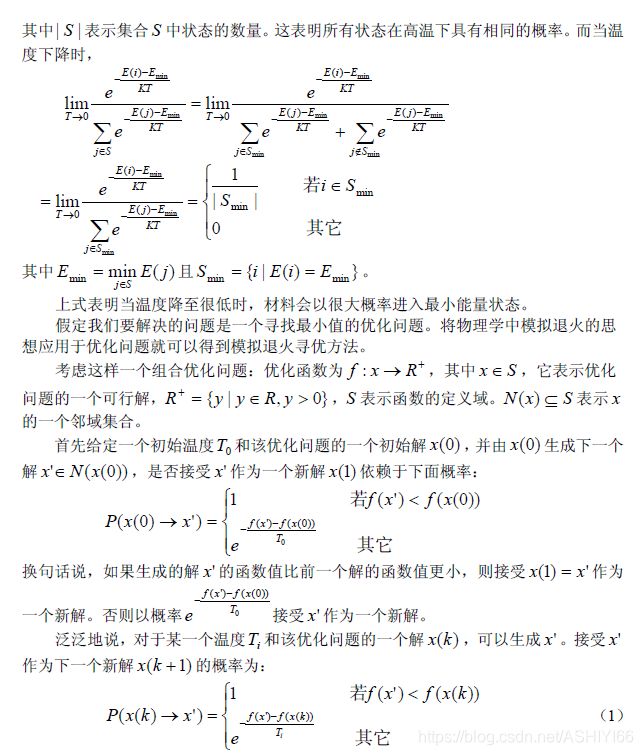
        模拟退火算法得益于材料的统计力学的研究成果。统计力学表明材料中粒子的不同结构对应于粒子的不同能量水平。在高温条件下，粒子的能量较高，可以自由运动和重新排列。在低温条件下，粒子能量较低。如果从高温开始，非常缓慢地降温（这个过程被称为退火)，粒子就可以在每个温度下达到热平衡。当系统完全被冷却时，最终形成处于低能状态的晶体。

 代码实现

clear
clc
T=1000; %初始化温度值
T_min=1; %设置温度下界
alpha=0.99; %温度的下降率
num=1000; %颗粒总数
n=2; %自变量个数
sub=[-5,-5]; %自变量下限
up=[5,5]; %自变量上限
tu
for i=1:num
for j=1:n
x(i,j)=(up(j)-sub(j))*rand+sub(j);
    end
    fx(i,1)=fun(x(i,1),x(i,2));
end

%以最小化为例
[bestf,a]=min(fx);
bestx=x(a,:);
trace(1)=bestf;
while(T>T_min)
for i=1:num
for j=1:n
            xx(i,j)=(up(j)-sub(j))*rand+sub(j);
        end
        ff(i,1)=fun(xx(i,1),xx(i,2));
        delta=ff(i,1)-fx(i,1);
if delta<0
            fx(i,1)=ff(i,1);
x(i,:)=xx(i,:);
else
            P=exp(-delta/T);
if P>rand
                fx(i,1)=ff(i,1);
x(i,:)=xx(i,:);
            end
        end  
    end
if min(fx)

function z=fun(x,y)
z = x.^2 + y.^2 - 10*cos(2*pi*x) - 10*cos(2*pi*y) + 20;

function tu
[x,y] = meshgrid(-5:0.1:5,-5:0.1:5);
z = x.^2 + y.^2 - 10*cos(2*pi*x) - 10*cos(2*pi*y) + 20;
figure
mesh(x,y,z)
hold on
xlabel('x')
ylabel('y')
zlabel('z')
title('z =  x^2 + y^2 - 10*cos(2*pi*x) - 10*cos(2*pi*y) + 20')

clear
clc
num=689000; %颗粒总数
n=2; %自变量个数
sub=[-5,-5]; %自变量下限
up=[5,5]; %自变量上限
tu
x=zeros(num,n);
fx=zeros(num,1);
for i=1:num
for j=1:n
x(i,j)=(up(j)-sub(j))*rand+sub(j);
    end
    fx(i,1)=fun(x(i,1),x(i,2));
end

[bestf,a]=min(fx);
bestx=x(a,:);

disp('最优解为：')
disp(bestx)
disp('最优值为：')
disp(bestf)
hold on
plot3(bestx(1),bestx(2),bestf,'ro','LineWidth',5)

(*部分内容参考NHASMJ、数学建模算法与应用*)