遗传算法与进化策略的对比
基于对生物进化机制的模仿,共产生进化算法的四种典型模型:
①遗传算法 Genetic Algorithm,GA
②进化规划 Evolutionary Programming,EP
③遗传规划 Genetic Programming,GP
④进化策略 Evolution Strategy, E
一、遗传算法(GA)
遗传算法是仿真生物遗传学和自然选择机理,通过人工方式所构造的一类搜索算法,从某种程度上说遗传算法是对生物进化过程进行的数学方式仿真。
其主要思想是生物种群的生存过程普遍遵循达尔文进化准则,群体中的个体根据对环境的适应能力而被大自然所选择或淘汰。进化过程的结果反映在个体的结构上,其染色体包含若干基因,相应的表现型和基因型的联系体现了个体的外部特性与内部机理间逻辑关系。通过个体之间的交叉、变异来适应大自然环境。生物染色体用数学方式或计算机方式来体现就是一串数码,仍叫染色体,有时也叫个体;适应能力是对应着一个染色体的一个数值来衡量;染色体的选择或淘汰则按所面对的问题是求最大还是最小来进行。
其实本质上,遗传算法就是在一个解空间上,随机的给定一组解,这组解称为父亲种群,通过这组解的交叉,变异(一会再解释这几个概念),构建出新的解,称为下一代种群,然后在目前已有的所有解(父亲种群和下一代种群)中抽取表现好的解组成新的父亲种群,然后继续上面的过程,直到达到了迭代条件或者获取到了最优解(一般都是局部最优解)。
遗传算法的架构图:
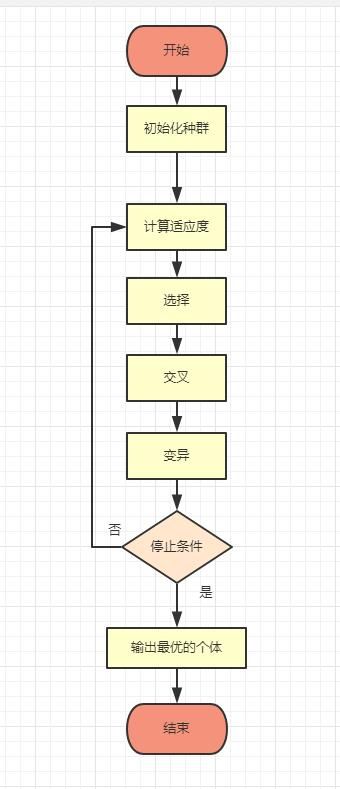
适应度
所谓的适应度,本质上可以理解为一个代价函数,或者一个规则,通过对初始种群中的个体计算适应度,能够得到对初始种群中的个体是否优劣的一个度量
选择
选择操作是根据种群中的个体的适应度函数值所度量的优、劣程度决定它在下一代是被淘汰还是被遗传。
交叉
交叉操作是将选择的两个个体p1p1作为父母节点,将两者的部分码值进行交换。假设有下面的两个节点的二进制编码表示:
![]()
随机产生一个1到7之间的随机数,假设为3,则将p1p1的低三位进行互换,如下图所示,就完成了交叉操作:
![]()
当然这个只是非常简单的交叉方法,业界常用的交叉方法为模拟二进制交叉,后面我们会继续介绍这种方法。
变异
变异操作就是改变节点p2p2的二进制编码的某些未知上的马尾的数值,如下所示:
| 1 | 1 | 0 | 1 | 1 | 1 | 1 |
随机产生一个1到8之间的随机数,假设为3,则将编码的第三位进行变异,将1变为0,如下图所示,就完成了交叉操作:
| 1 | 1 | 0 | 1 | 1 | 0 | 1 |
这个依旧是一种简单的变异操作,业界常用的变异操作方法有高斯变异,柯西变异等。
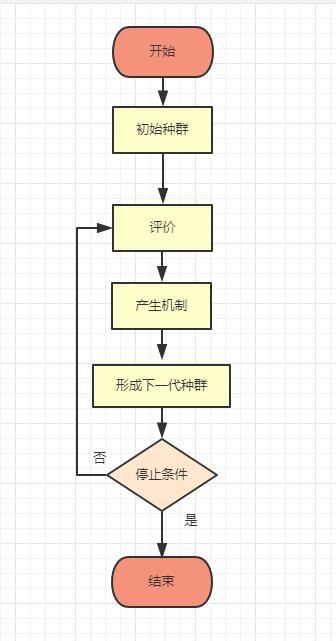
二、进化策略(ES)
与遗传算法对比的相同点:进化策略的思路与遗传算法相似,二者都是利用进化理论进行优化,即利用遗传信息一代代传承变异,通过适者生存的理论,保存适应度高的个体,得到最优解。
不同点:
1.DNA序列采用实数编码,而非0-1二进制码
2.变异时无法进行简单的0-1互换,思考:实数值该怎么变?随机?
变异思路:为DNA序列上的每一个实数值添加变异强度。根据这个变异强度决定DNA序列上的实数值该变成多少
3.编码:
由第2点可知,进化策略在编码时,不仅要有表示解决方案的实数编码链A1,还得有一条表示每个实属值对应的变异强度值组成的链A2(也就是说,遗传给后代的信息有两种)
4.交叉:
两条链都要交叉,即A1与B1交叉形成表示子代解决方案的C1链,A2与B2交叉形成表示C1链对应位置实数值变异强度的C2链(父:A,母:B,子:C)
5.C1链上值的变异方法:
将C1链上的值看作正态分布的均值μ;
将C2链上变异强度值看作标准差σ;
用正态分布产生一个与C1链上选定位置相近的数,进行替换;
6.C2链上值的变异方法:
因为随着不断遗传迭代,种群中个体1号链的值不断逼近最优解,变异的强度也应当不断减小。所以也需要根据需求自定义2号链的变异方法。
7.选择:
将生成的孩子加入父代中,形成一个包含两代DNA的种群U;
对U种群中每个DNA序列的1号链(表示解决方案)进行fitness计算(打分),并根据分值从大到小排列(用U‘表示排列后的混合种群);
截取U’中的分值高的前n位(n表示一代种群中的个体数目)形成新种群;
1、遗传算法采用二进制编码杂交;而进化策略使用实数。
2、遗传算法采用二进制0->1,1->实现变异;而进化策略则使用变异强度实现变异。
3、遗传算法仅需要一条编码链,用于存储个体的基因;进化策略在编码时,不仅要有实数编码链,还要有变异强度编码链。
4、遗传算法在交叉繁殖的时候,仅实现基因的交叉;进化策略则要实现两条链的交叉,父母辈的实数链交叉形成子辈的实数链,变异强度编码链交叉形成子辈的变异强度编码链。
5、遗传算法在变异时,随机选择基因段变异;进化策略则是将实数链上的实数值看作正态分布的均值μ,将变异强度编码链上变异强度值看作正态分布的标准差σ。
6、遗传算法在自然选择时,通过轮盘赌实现自然选择;进化策略则将子种群加入到父种群中,按照适应度排序,直接选出适应度最大的pop_size个个体。
进化策略代码
import numpy as np
import matplotlib.pyplot as plt
# 每个个体的长度
GENE_SIZE = 1
# 每个基因的范围
GENE_BOUND = [0, 5]
# 200代
N_GENERATIONS = 200
# 种群的大小
POP_SIZE = 100
# 每一代生成50个孩子
N_KID = 50
# 寻找函数的最大值
def F(x):
return np.sin(10*x)*x + np.cos(2*x)*x
class ES():
def __init__(self,gene_size,pop_size,n_kid):
# 基因长度代表字符串的长度
self.gene_size = gene_size
# 种群的大小代表种群中有几个个体
self.pop_size = pop_size
self.n_kid = n_kid
self.init_pop()
print(self.pop)
# 降到一维
def get_fitness(self):
return self.pred.flatten()
# 初始化种群
def init_pop(self):
self.pop = dict(DNA=5 * np.random.rand(1, self.gene_size).repeat(POP_SIZE, axis=0),
mut_strength=np.random.rand(POP_SIZE, self.gene_size))
# 更新后代
def make_kid(self):
# DNA指的是当前孩子的基因
# mut_strength指的是变异强度
self.kids = {'DNA': np.empty((self.n_kid, self.gene_size)),
'mut_strength': np.empty((self.n_kid, self.gene_size))}
for kv, ks in zip(self.kids['DNA'], self.kids['mut_strength']):
# 杂交,随机选择父母
p1, p2 = np.random.choice(self.pop_size, size=2, replace=False)
# 选择杂交点
cp = np.random.randint(0, 2, self.gene_size, dtype=np.bool)
# 当前孩子基因的杂交结果
kv[cp] = self.pop['DNA'][p1, cp]
kv[~cp] = self.pop['DNA'][p2, ~cp]
# 当前孩子变异强度的杂交结果
ks[cp] = self.pop['mut_strength'][p1, cp]
ks[~cp] = self.pop['mut_strength'][p2, ~cp]
# 变异强度要大于0,并且不断缩小
ks[:] = np.maximum(ks + (np.random.rand()-0.5), 0.)
kv += ks * np.random.randn()
# 截断
kv[:] = np.clip(kv,GENE_BOUND[0],GENE_BOUND[1])
# 淘汰低适应度后代
def kill_bad(self):
# 进行vertical垂直叠加
for key in ['DNA', 'mut_strength']:
self.pop[key] = np.vstack((self.pop[key], self.kids[key]))
# 计算fitness
self.pred = F(self.pop['DNA'])
fitness = self.get_fitness()
# 读出按照降序排列fitness的索引
max_index = np.argsort(-fitness)
# 选择适应度最大的50个个体
good_idx = max_index[:POP_SIZE]
for key in ['DNA', 'mut_strength']:
self.pop[key] = self.pop[key][good_idx]
test1 = ES(gene_size = GENE_SIZE,pop_size = POP_SIZE,n_kid = N_KID)
plt.ion()
x = np.linspace(*GENE_BOUND, 200)
plt.plot(x, F(x))
for _ in range(N_GENERATIONS):
# 画图部分
if 'sca' in globals(): sca.remove()
sca = plt.scatter(test1.pop['DNA'], F(test1.pop['DNA']), s=200, lw=0, c='red', alpha=0.5)
plt.pause(0.05)
# ES更新
kids = test1.make_kid()
pop = test1.kill_bad()
plt.ioff(); plt.show()
遗传算法代码
import numpy as np
import math
import random
def binarytodecimal(binary): # 将二进制转化为十进制,x的范围是[0,10]
total = 0
for j in range(len(binary)):
total += binary[j] * (2**j)
total = total * 10 / 1023
return total
def pop_b2d(pop): # 将整个种群转化成十进制
temppop = []
for i in range(len(pop)):
t = binarytodecimal(pop[i])
temppop.append(t)
return temppop
def calobjvalue(pop): # 计算目标函数值
x = np.array(pop_b2d(pop))
return count_function(x)
def count_function(x):
y = np.sin(x) + np.cos(5 * x) - x**2 + 2*x
return y
def calfitvalue(objvalue):
# 转化为适应值,目标函数值越大越好
# 在本例子中可以直接使用函数运算结果为fit值,因为我们求的是最大值
# 在实际应用中需要处理
for i in range(len(objvalue)):
if objvalue[i] < 0:
objvalue[i] = 0
return objvalue
def best(pop, fitvalue):
#找出适应函数值中最大值,和对应的个体
bestindividual = pop[0]
bestfit = fitvalue[0]
for i in range(1,len(pop)):
if(fitvalue[i] > bestfit):
bestfit = fitvalue[i]
bestindividual = pop[i]
return [bestindividual, bestfit]
def selection(pop, fit_value):
probability_fit_value = []
# 适应度总和
total_fit = sum(fit_value)
# 求每个被选择的概率
probability_fit_value = np.array(fit_value) / total_fit
# 概率求和排序
cum_sum_table = cum_sum(probability_fit_value)
# 获取与pop大小相同的一个概率矩阵,其每一个内容均为一个概率
# 当概率处于不同范围时,选择不同的个体。
choose_probability = np.sort([np.random.rand() for i in range(len(pop))])
fitin = 0
newin = 0
newpop = pop[:]
# 轮盘赌法
while newin < len(pop):
# 当概率处于不同范围时,选择不同的个体。
# 如个体适应度分别为1,2,3,4,5的种群
# 利用np.random.rand()生成一个随机数,当其处于0-0.07时
# 选择个体1,当其属于0.07-0.2时选择个体2,以此类推。
if (choose_probability[newin] < cum_sum_table[fitin]):
newpop[newin] = pop[fitin]
newin = newin + 1
else:
fitin = fitin + 1
# pop里存在重复的个体
pop = newpop[:]
def cum_sum(fit_value):
# 输入[1, 2, 3, 4, 5],返回[1,3,6,10,15]
temp = fit_value[:]
temp2 = fit_value[:]
for i in range(len(temp)):
temp2[i] = (sum(temp[:i + 1]))
return temp2
def crossover(pop, pc):
# 按照一定概率杂交
pop_len = len(pop)
for i in range(pop_len - 1):
# 判断是否达到杂交几率
if (np.random.rand() < pc):
# 随机选取杂交点,然后交换结点的基因
individual_size = len(pop[0])
# 随机选择另一个个体进行杂交
destination = np.random.randint(0,pop_len)
# 生成每个基因进行交换的结点
crosspoint = np.random.randint(0,2,size = individual_size)
# 找到这些结点的索引
index = np.argwhere(crosspoint==1)
# 进行赋值
pop[i,index] = pop[destination,index]
def mutation(pop, pm):
pop_len = len(pop)
individual_size = len(pop[0])
# 每条染色体随便选一个杂交
for i in range(pop_len):
for j in range(individual_size):
if (np.random.rand() < pm):
if (pop[i][j] == 1):
pop[i][j] = 0
else:
pop[i][j] = 1
# 用遗传算法求函数最大值,组合交叉的概率时0.6,突变的概率为0.001
# y = np.sin(x) + np.cos(5 * x) - x**2 + 2*x
popsize = 50 # 种群的大小
pc = 0.6 # 两个个体交叉的概率
pm = 0.001 # 基因突变的概率
gene_size = 10 # 基因长度为10
generation = 100 # 繁殖100代
results = []
bestindividual = []
bestfit = 0
fitvalue = []
pop = np.array([np.random.randint(0,2,size = gene_size) for i in range(popsize)])
for i in range(generation): # 繁殖100代
objvalue = calobjvalue(pop) # 计算种群中目标函数的值
fitvalue = calfitvalue(objvalue) # 计算个体的适应值
[bestindividual, bestfit] = best(pop, fitvalue) # 选出最好的个体和最好的适应值
results.append([bestfit,binarytodecimal(bestindividual)]) # 每次繁殖,将最好的结果记录下来
selection(pop, fitvalue) # 自然选择,淘汰掉一部分适应性低的个体
crossover(pop, pc) # 交叉繁殖
mutation(pop, pc) # 基因突变
results.sort()
print(results[-1]) #打印使得函数取得最大的个体,和其对应的适应度