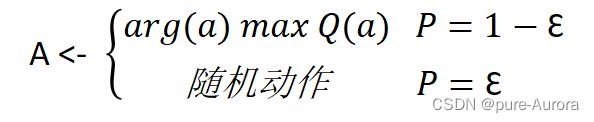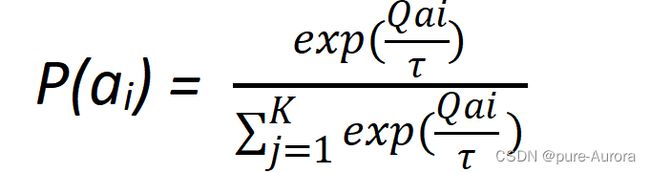强化学习笔记（一）

最近在学习有关强化学习的一些内容，写点东西记录一下

第一篇笔记主要是关于强化学习的概念，以及入门的一些基础进行记录。

目录

强化学习是什么：

由一个实例认识强化学习

多臂赌博机问题               

 Ԑ -greedy 策略

玻尔兹曼策略

代码实现

---

强化学习是什么：

强化学习是一种基于反馈的学习，即存在一个智能体，能够感知环境，根据环境状态做出动作，并从环境接收反馈信息，以此调整自身的行动策略。

强化学习是学习状态和行为之间的映射关系，以使得数值回报达到最大化。在未知采取何种行为的情况下，学习者必须通过不断的尝试才能发现采取那种行为能够产生最大回报。即从和交互中进行学习以达到期望目标的方法。

强化学习的主角：

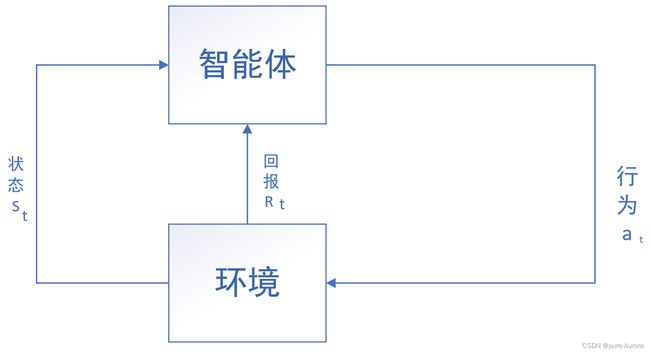
学习者称为 智能体 或 玩家 （agent）与智能体交互的外部被称为 环境(enviroment)

智能体应选择相应的行为来使得环境所表现的回报最大化。假设离散时间序列 t=0 , 1 , 2, 3,...。

对于每一个时刻t，都存在一个智能体从环境中接受一个状态st.

同样定义一个at来表示智能体在时刻t所采取的行为。在下一刻，at作为智能体行为的结果，然后接收回报rt+1，如上图所示，在每一时刻，智能体完成的从状态到每种可能行为的选择改路之间的映射，称为智能体策略 记为πt，      

πt(s,a)记为在 st = s 的时刻 at = a 的概率。

强化学习具体反映了如何根据其经验法改变策略，使得长期运行中接收的回报总量达到了最大化。

由一个实例认识强化学习

多臂赌博机问题               

多臂赌博机有多个摇臂，赌徒在投入一个硬币后可选择按下其中一个摇臂，每个摇臂以一定的概率吐出硬币，但这个概率赌徒并不知道。赌徒的目标是通过一定的策略最大化自己的奖赏，即获得最多的硬币。

多臂赌博机的问题是：假设玩家共有N次摇动摇臂的机会，每次如何选择摇动那个臂使得N轮后得到的硬币最多。

对于这个问题，如果你提前知道每个臂对应出多少硬币，那么每一次都摇动这个臂就可以了，但是，问题是你并不知道摇动哪个臂能获得最多的硬币。这个时候，我们应该采用什么样的策略呢？

首先的直观想法就是：既然不知道那个臂吐得多，就可以先对每一个臂都尝试几次，找出那个臂吐得最多，然后一直摇这个多的臂。

上述想法已经包含了算法学习最基本的两个过程：采集数据和学习。对每个臂进行尝试就是采集数据。学习就是利用这些数据知道那个臂会突出最多的金币。

现在假设赌博机的臂数K=3 ， A为一个动作集合，a∈A， 那么A = {1,2,3}

同理 K = k， 则A={1,2,3,...k}

用回报r表示摇动赌博机后获得的金币数目。Q(a)表示摇动动作a所获得的金币的平均回报。则Q(a) =  ,其中n 为摇动动作a的总次数。 设R(a)为总回报。

那么总结起来的策略就是：

1 初始化每个动作的总回报R(a)，以及摇动该动作的次数N(a)。

2 每个臂都摇动na 次，计算每个摇臂总的金币数。

3 算出使得回报最大的那个臂，一直摇他

到这我们会发现，这不就是贪婪策略么，但是上述这个策略很明显有一些问题：

首先，我们不应以总的回报作为目标，而是应该以平均回报作为目标

其次，当前这个摇臂真的是最好的摇臂么？很明显不一定，因为我们只取了有限几次的实验结果，无法保证这几次摇出来的就能真正的代表他们的具体好坏，所以我们除了要关注当前这个最大的臂，还要留出来一定概率取摇动其他的臂，以便发现更好的臂。

这就对应着强化学习中的重要概念，“利用”(exploitation)和“探索”(exploratation)平衡。

 Ԑ -greedy 策略

最常见的平衡利用和探索的概念就是Ԑ-greedy策略，用公式可以表示为：

即每次选择要哪条摇动机械臂的时候，应该先以 1-Ԑ 的概率摇动当前均值最大的机械臂，再以 Ԑ 的概率在所有的动作中均匀随机地选择动作。这样做的目的是在有限的次数中得到尽可能多的回报，同时不失去找到最好的臂的机会。

玻尔兹曼策略

前面介绍的Ԑ-greedy策略，“利用”部分的概率，将当前最优与其他动作进行概率选择，然而其他概率也有好坏之分，玻尔兹曼，对其进行了优化

其中τ为温度调节参数，可用来调节探索和利用的比例。τ越小，玻尔兹曼策略越接近贪婪策略，利用所占的比例越大，探索越少。τ越大，玻尔兹曼策略就越接近均匀分布策略，探索就越多。

代码实现

以三臂老虎机为例，搭建出动作模型

    def step(self,a):                               #模拟多臂机是如何给出回报的
        r = 0                                       #人为设定回报是按着正态分布进行的
        if a == 1 :
            r = np.random.normal(1, 1)              #随机生成回报
        if a == 2 :
            r = np.random.normal(2, 1)
        if a == 3 :
            r = np.random.normal(1.5, 1)
        return r

    def choose_action(self,policy, t):       #选择动作函数
        action = 0
        if policy == 'e_greedy':                    #e-greedy贪婪
            if np.random.random() < t:
                action = np.random.randint(1, 4)
            else:
                action = np.argmax(self.q) + 1
        if policy == 'boltzmann':                   #玻尔兹曼
            tau = t
            p = (np.exp(self.q/tau))/(np.sum(np.exp(self.q/tau)))
            action = np.random.choice([1,2,3], p = p)

        return action

主要在训练过程中，要使得与环境进行交互

    def train(self, play_total, policy,t):  #训练过程
        reward_1 = []
        reward_2 = []
        reward_3 = []
        for i in range(play_total):
            action = 0
            if policy == 'e_greedy':
                action = self.choose_action(policy , t)
            if policy == 'boltzmann':
                action = self.choose_action(policy, t)
            self.a = action                         #与环境交互
            self.r = self.step(self.a)
            self.counts = self.counts + 1
            self.q[self.a - 1] = (self.q[self.a - 1]*self.action_counts[self.a - 1] + self .r)/(self.action_counts[self.a -1] + 1)
            self.action_counts[self.a - 1 ] = self.action_counts[self.a - 1 ] + 1
            reward_1.append([self.q[0]])
            reward_2.append([self.q[1]])
            reward_3.append([self.q[2]])
            self.sum_reward = self.sum_reward + self.r
            self.reward_history.append([self.sum_reward])
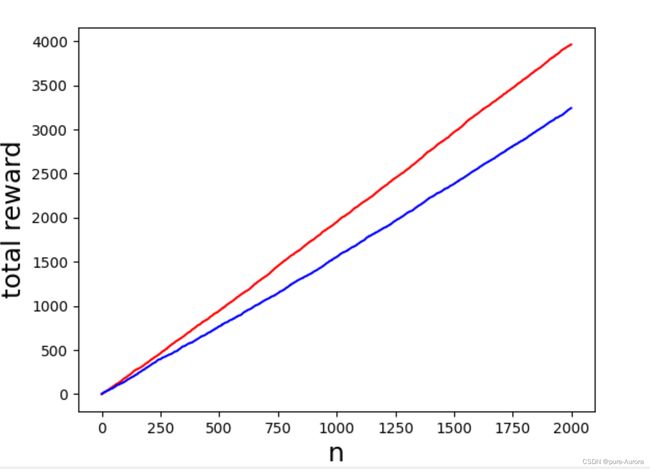
            self.counts_history.append(i)

经实际代码运行发现玻尔兹曼未必优于 Ԑ-greedy策略

红色代表 Ԑ-greedy策略 ， 蓝色代表boltzmann

具体的二者之间谁更好还要结合调节二者的参数去判断