Tensorflow学习笔记(三):神经网络八股
本文是个人的学习笔记,是跟随北大曹健老师的视频课学习的
附:bilibili课程链接 和 MOOC课程链接 以及 源码下载链接 (提取码:mocm)
文章目录
- 一、神经网络搭建八股:六步法
-
- 1. `import`
- 2. 导入dataset
- 3. `model = tf.keras.models.Sequential([网络结构])`:描述各层网络
-
- 拉直层
- 全连接层
- 卷积层
- LSTM层
- 4. `model.compile`:配置训练方法
-
- 调用格式
- optimizer=
- loss=
- metrics=
- 5. `model.fit`:训练
-
- 调用格式
- 6. `model.summary`:打印网络结构、参数统计
-
- 调用格式
- 二、举例与讨论
-
- 1. 复现:iris分类代码
-
- (1)搭建网络八股sequential进行分类
- (2)搭建网络八股class进行分类
- 2. MNIST数据集及分类
-
- (1)认识数据集
- (2)搭建神经网络进行手写数字识别
- 3. 练习:Fashion数据集及分类
-
- (1)认识数据集
- (2)搭建神经网络训练
- 三、网络八股功能扩展
-
- 复盘六步法
-
- (1)总结
- (2)限制
- 1. 自制数据集
-
- 功能代码实现
- 八股修改
- 2. 数据增强
-
- 核心函数
- 相关代码
- 结果说明
- 3. 断点续训
-
- 代码实现
- 使用效果
- 4. 参数提取
-
- 直接查看
- 保存本地
- 5. Acc/Loss可视化
-
- 代码实现
- 结果展示
- 四、从训练到实际
-
- 训练源码
- 应用源码
- 使用效果
一、神经网络搭建八股:六步法
1. import
2. 导入dataset
3. model = tf.keras.models.Sequential([网络结构]):描述各层网络
拉直层
- 调用代码:
tf.keras.layers.Flatten() - 不含计算,仅仅形状转换,把输入特征 一维数组
全连接层
- 调用代码:
tf.keras.layers.Dense(神经元个数, activation=激活函数, kernel_regularizer=正则化方式) - 激活函数:
relu,softmax,sigmoid,tanh - 正则化方式:
tf.keras.regularizers.l1(),tf.keras.regularizers.l2()
卷积层
- 调用代码:
tf.keras.layers.Conv2D(filters=卷积核个数, kernel_size=卷积核尺寸, strides=卷积步长, padding="valid" or "same")
LSTM层
- 调用代码:
tf.keras.layers.LSTM()
4. model.compile:配置训练方法
调用格式
model.compile(optimizer=优化器, loss=损失函数, metrics=["准确率"])
optimizer=
'sgd'ortf.keras.optimizers.SGD(lr=, momentum=)'adagrad'ortf.keras.optimizers.Adagrad(lr=)'adadelta'ortf.keras.optimizers.Adadelta(lr=)'adam'ortf.keras.optimizers.Adam(lr=, beta_1=0.9, beta_2=0.999)
loss=
'mse'ortf.keras.losses.MeanSquaredError()'sparse_categorical_crossentropy'ortf.keras.losses.SparseCategoricalCrossentropy(from_logits=False):输出前经过概率分布为False,没有则为True
metrics=
根据数据标签 y y y和预测值 y ^ \hat y y^的形式确定参数值
'accuracy': y y y和 y ^ \hat y y^都是数值,如 y = [ 1 ] , y ^ = [ 1 ] y=[1], ~\hat y=[1] y=[1], y^=[1]'categorical_accuracy': y y y和 y ^ \hat y y^都是独热编码(概率分布),如 y = [ 0 , 1 , 0 ] , y ^ = [ 0.256 , 0.695 , 0.048 ] y=[0,1,0], ~\hat y=[0.256,0.695,0.048] y=[0,1,0], y^=[0.256,0.695,0.048]'sparse_categorical_accuracy': y y y是数值, y ^ \hat y y^是独热编码(概率分布),如 y = [ 1 ] , y ^ = [ 0.256 , 0.695 , 0.048 ] y=[1],~ \hat y=[0.256,0.695,0.048] y=[1], y^=[0.256,0.695,0.048]
5. model.fit:训练
调用格式
model.fit(训练集输入特征, 训练集标签, batch_size=, epochs=, validation_data=(测试集的输入特征, 测试集的标签), validation_split=从训练集划分多少比例给测试集, validation_freq=多少次epoch测试一次)
6. model.summary:打印网络结构、参数统计
调用格式
model.summary()
二、举例与讨论
看到这里已经有些迷茫了。。。所以通过一个例子来看看是如何“搭积木”的
1. 复现:iris分类代码
(1)搭建网络八股sequential进行分类
- 源码
# import
import numpy as np
import tensorflow as tf
from sklearn import datasets
# 导入dataset
iris = datasets.load_iris()
x = iris.data
y = iris.target
np.random.seed(76)
np.random.shuffle(x)
np.random.seed(76)
np.random.shuffle(y)
tf.random.set_seed(76)
# model = models.Sequential
model = tf.keras.models.Sequential([
tf.keras.layers.Dense(
3,
activation='softmax',
kernel_regularizer=tf.keras.regularizers.l2()
)
])
# model.compile
model.compile(
optimizer=tf.keras.optimizers.SGD(lr=0.1),
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=False),
metrics=['sparse_categorical_accuracy']
)
# model.fit
model.fit(
x, y, batch_size=32, epochs=500,
validation_split=0.2,
validation_freq=20
)
# model.summary
model.summary()
- 结果展示
Epoch 1/500
4/4 [==============================] - 0s 5ms/step - loss: 4.7593 - sparse_categorical_accuracy: 0.3417
Epoch 2/500
4/4 [==============================] - 0s 0s/step - loss: 3.2841 - sparse_categorical_accuracy: 0.3417
Epoch 3/500
4/4 [==============================] - 0s 0s/step - loss: 2.0309 - sparse_categorical_accuracy: 0.3417
Epoch 4/500
4/4 [==============================] - 0s 0s/step - loss: 1.2765 - sparse_categorical_accuracy: 0.3500
Epoch 5/500
4/4 [==============================] - 0s 0s/step - loss: 0.9750 - sparse_categorical_accuracy: 0.3750
Epoch 6/500
4/4 [==============================] - 0s 0s/step - loss: 0.8396 - sparse_categorical_accuracy: 0.4583
Epoch 7/500
4/4 [==============================] - 0s 5ms/step - loss: 0.7756 - sparse_categorical_accuracy: 0.6000
Epoch 8/500
4/4 [==============================] - 0s 0s/step - loss: 0.7225 - sparse_categorical_accuracy: 0.4250
Epoch 9/500
4/4 [==============================] - 0s 0s/step - loss: 0.6942 - sparse_categorical_accuracy: 0.4667
Epoch 10/500
4/4 [==============================] - 0s 5ms/step - loss: 0.6758 - sparse_categorical_accuracy: 0.4167
Epoch 11/500
4/4 [==============================] - 0s 0s/step - loss: 0.6634 - sparse_categorical_accuracy: 0.4583
Epoch 12/500
4/4 [==============================] - 0s 0s/step - loss: 0.6571 - sparse_categorical_accuracy: 0.4667
Epoch 13/500
4/4 [==============================] - 0s 0s/step - loss: 0.6481 - sparse_categorical_accuracy: 0.4917
Epoch 14/500
4/4 [==============================] - 0s 0s/step - loss: 0.6457 - sparse_categorical_accuracy: 0.4417
Epoch 15/500
4/4 [==============================] - 0s 0s/step - loss: 0.6406 - sparse_categorical_accuracy: 0.4667
Epoch 16/500
4/4 [==============================] - 0s 0s/step - loss: 0.6432 - sparse_categorical_accuracy: 0.4833
Epoch 17/500
4/4 [==============================] - 0s 5ms/step - loss: 0.6324 - sparse_categorical_accuracy: 0.5750
Epoch 18/500
4/4 [==============================] - 0s 0s/step - loss: 0.6320 - sparse_categorical_accuracy: 0.4917
Epoch 19/500
4/4 [==============================] - 0s 0s/step - loss: 0.6275 - sparse_categorical_accuracy: 0.4750
Epoch 20/500
4/4 [==============================] - 0s 52ms/step - loss: 0.6239 - sparse_categorical_accuracy: 0.5583 - val_loss: 0.6717 - val_sparse_categorical_accuracy: 0.3667
...
Epoch 481/500
4/4 [==============================] - 0s 0s/step - loss: 0.3849 - sparse_categorical_accuracy: 0.9750
Epoch 482/500
4/4 [==============================] - 0s 0s/step - loss: 0.3806 - sparse_categorical_accuracy: 0.9750
Epoch 483/500
4/4 [==============================] - 0s 0s/step - loss: 0.3830 - sparse_categorical_accuracy: 0.9833
Epoch 484/500
4/4 [==============================] - 0s 0s/step - loss: 0.3804 - sparse_categorical_accuracy: 0.9833
Epoch 485/500
4/4 [==============================] - 0s 0s/step - loss: 0.3829 - sparse_categorical_accuracy: 0.9833
Epoch 486/500
4/4 [==============================] - 0s 0s/step - loss: 0.3807 - sparse_categorical_accuracy: 0.9750
Epoch 487/500
4/4 [==============================] - 0s 0s/step - loss: 0.3802 - sparse_categorical_accuracy: 0.9833
Epoch 488/500
4/4 [==============================] - 0s 0s/step - loss: 0.3817 - sparse_categorical_accuracy: 0.9833
Epoch 489/500
4/4 [==============================] - 0s 0s/step - loss: 0.3805 - sparse_categorical_accuracy: 0.9750
Epoch 490/500
4/4 [==============================] - 0s 5ms/step - loss: 0.3798 - sparse_categorical_accuracy: 0.9833
Epoch 491/500
4/4 [==============================] - 0s 0s/step - loss: 0.3807 - sparse_categorical_accuracy: 0.9833
Epoch 492/500
4/4 [==============================] - 0s 0s/step - loss: 0.3801 - sparse_categorical_accuracy: 0.9833
Epoch 493/500
4/4 [==============================] - 0s 0s/step - loss: 0.3793 - sparse_categorical_accuracy: 0.9833
Epoch 494/500
4/4 [==============================] - 0s 0s/step - loss: 0.3817 - sparse_categorical_accuracy: 0.9917
Epoch 495/500
4/4 [==============================] - 0s 0s/step - loss: 0.3800 - sparse_categorical_accuracy: 0.9833
Epoch 496/500
4/4 [==============================] - 0s 0s/step - loss: 0.3793 - sparse_categorical_accuracy: 0.9750
Epoch 497/500
4/4 [==============================] - 0s 5ms/step - loss: 0.3811 - sparse_categorical_accuracy: 0.9667
Epoch 498/500
4/4 [==============================] - 0s 0s/step - loss: 0.3790 - sparse_categorical_accuracy: 0.9750
Epoch 499/500
4/4 [==============================] - 0s 0s/step - loss: 0.3791 - sparse_categorical_accuracy: 0.9750
Epoch 500/500
4/4 [==============================] - 0s 10ms/step - loss: 0.3787 - sparse_categorical_accuracy: 0.9750 - val_loss: 0.4051 - val_sparse_categorical_accuracy: 0.9667
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense (Dense) (None, 3) 15
=================================================================
Total params: 15
Trainable params: 15
Non-trainable params: 0
_________________________________________________________________
使用sequential的局限:无法实现带有跳连的非顺序网络结构
解决方法:使用class搭建网络
(2)搭建网络八股class进行分类
- 源码
仅需将上述源码的model = models.Sequential部分更改为如下的class model即可
# class model
class irisModel(tf.keras.Model):
# 构建类
def __init__(self):
super(irisModel, self).__init__()
# 定义网络结构块
self.layer = tf.keras.layers.Dense(
3,
activation='softmax',
kernel_regularizer=tf.keras.regularizers.l2()
)
def call(self, x):
# 调用网络结构块,实现前向传播
y = self.layer(x)
return y
model = irisModel() # 实例化对象
- 结果展示
Epoch 1/500
4/4 [==============================] - 0s 5ms/step - loss: 1.0251 - sparse_categorical_accuracy: 0.5750
Epoch 2/500
4/4 [==============================] - 0s 0s/step - loss: 0.9047 - sparse_categorical_accuracy: 0.4917
Epoch 3/500
4/4 [==============================] - 0s 5ms/step - loss: 0.8671 - sparse_categorical_accuracy: 0.5083
Epoch 4/500
4/4 [==============================] - 0s 0s/step - loss: 0.8382 - sparse_categorical_accuracy: 0.4833
Epoch 5/500
4/4 [==============================] - 0s 0s/step - loss: 0.8366 - sparse_categorical_accuracy: 0.5083
Epoch 6/500
4/4 [==============================] - 0s 0s/step - loss: 0.8193 - sparse_categorical_accuracy: 0.4750
Epoch 7/500
4/4 [==============================] - 0s 0s/step - loss: 0.8217 - sparse_categorical_accuracy: 0.4917
Epoch 8/500
4/4 [==============================] - 0s 0s/step - loss: 0.8032 - sparse_categorical_accuracy: 0.4917
Epoch 9/500
4/4 [==============================] - 0s 0s/step - loss: 0.7979 - sparse_categorical_accuracy: 0.5000
Epoch 10/500
4/4 [==============================] - 0s 5ms/step - loss: 0.7900 - sparse_categorical_accuracy: 0.4917
Epoch 11/500
4/4 [==============================] - 0s 0s/step - loss: 0.7835 - sparse_categorical_accuracy: 0.4917
Epoch 12/500
4/4 [==============================] - 0s 0s/step - loss: 0.7804 - sparse_categorical_accuracy: 0.4917
Epoch 13/500
4/4 [==============================] - 0s 5ms/step - loss: 0.7709 - sparse_categorical_accuracy: 0.5000
Epoch 14/500
4/4 [==============================] - 0s 0s/step - loss: 0.7676 - sparse_categorical_accuracy: 0.4750
Epoch 15/500
4/4 [==============================] - 0s 0s/step - loss: 0.7609 - sparse_categorical_accuracy: 0.5083
Epoch 16/500
4/4 [==============================] - 0s 0s/step - loss: 0.7633 - sparse_categorical_accuracy: 0.4917
Epoch 17/500
4/4 [==============================] - 0s 5ms/step - loss: 0.7491 - sparse_categorical_accuracy: 0.5083
Epoch 18/500
4/4 [==============================] - 0s 0s/step - loss: 0.7477 - sparse_categorical_accuracy: 0.5167
Epoch 19/500
4/4 [==============================] - 0s 0s/step - loss: 0.7409 - sparse_categorical_accuracy: 0.4917
Epoch 20/500
4/4 [==============================] - 0s 52ms/step - loss: 0.7351 - sparse_categorical_accuracy: 0.5000 - val_loss: 0.7733 - val_sparse_categorical_accuracy: 0.4333
...
Epoch 481/500
4/4 [==============================] - 0s 5ms/step - loss: 0.3890 - sparse_categorical_accuracy: 0.9750
Epoch 482/500
4/4 [==============================] - 0s 0s/step - loss: 0.3847 - sparse_categorical_accuracy: 0.9833
Epoch 483/500
4/4 [==============================] - 0s 0s/step - loss: 0.3874 - sparse_categorical_accuracy: 0.9833
Epoch 484/500
4/4 [==============================] - 0s 5ms/step - loss: 0.3845 - sparse_categorical_accuracy: 0.9833
Epoch 485/500
4/4 [==============================] - 0s 0s/step - loss: 0.3872 - sparse_categorical_accuracy: 0.9833
Epoch 486/500
4/4 [==============================] - 0s 0s/step - loss: 0.3847 - sparse_categorical_accuracy: 0.9750
Epoch 487/500
4/4 [==============================] - 0s 0s/step - loss: 0.3844 - sparse_categorical_accuracy: 0.9833
Epoch 488/500
4/4 [==============================] - 0s 0s/step - loss: 0.3858 - sparse_categorical_accuracy: 0.9833
Epoch 489/500
4/4 [==============================] - 0s 0s/step - loss: 0.3845 - sparse_categorical_accuracy: 0.9750
Epoch 490/500
4/4 [==============================] - 0s 0s/step - loss: 0.3836 - sparse_categorical_accuracy: 0.9833
Epoch 491/500
4/4 [==============================] - 0s 0s/step - loss: 0.3848 - sparse_categorical_accuracy: 0.9833
Epoch 492/500
4/4 [==============================] - 0s 0s/step - loss: 0.3838 - sparse_categorical_accuracy: 0.9833
Epoch 493/500
4/4 [==============================] - 0s 0s/step - loss: 0.3831 - sparse_categorical_accuracy: 0.9833
Epoch 494/500
4/4 [==============================] - 0s 5ms/step - loss: 0.3857 - sparse_categorical_accuracy: 0.9750
Epoch 495/500
4/4 [==============================] - 0s 0s/step - loss: 0.3838 - sparse_categorical_accuracy: 0.9833
Epoch 496/500
4/4 [==============================] - 0s 0s/step - loss: 0.3831 - sparse_categorical_accuracy: 0.9833
Epoch 497/500
4/4 [==============================] - 0s 0s/step - loss: 0.3849 - sparse_categorical_accuracy: 0.9833
Epoch 498/500
4/4 [==============================] - 0s 5ms/step - loss: 0.3828 - sparse_categorical_accuracy: 0.9833
Epoch 499/500
4/4 [==============================] - 0s 0s/step - loss: 0.3828 - sparse_categorical_accuracy: 0.9833
Epoch 500/500
4/4 [==============================] - 0s 5ms/step - loss: 0.3822 - sparse_categorical_accuracy: 0.9750 - val_loss: 0.4033 - val_sparse_categorical_accuracy: 0.9667
Model: "iris_model"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense (Dense) multiple 15
=================================================================
Total params: 15
Trainable params: 15
Non-trainable params: 0
_________________________________________________________________
两种方法搭建出来的网络训练结果是相同的
2. MNIST数据集及分类
(1)认识数据集
- 数据集在哪里?
tensorflow库中就有MNIST数据集,我们可以用如下代码导入
# 导入数据集
mnist = tf.keras.datasets.mnist
(x_train, y_train), (x_test, y_test) = mnist.load_data()
- 训练集和测试集是怎么组成的?
想要在MNIST数据集上训练,就首先要认识训练集和测试集是什么“样子”,print出来数据集的shape看看
# 数据集形状
print("x_train.shape:", x_train.shape)
print("y_train.shape:", y_train.shape)
print("x_test.shape:", x_test.shape)
print("y_test.shape:", y_test.shape)
结果是
x_train.shape: (60000, 28, 28)
y_train.shape: (60000,)
x_test.shape: (10000, 28, 28)
y_test.shape: (10000,)
也就是说,MNIST是由含60000个元素的训练集和含10000个元素的测试集组成的。对于每一个元素而言,对应的数据为一个2828(=784)大小的二维数组,对应的标签为一个11的数值
- 那数据和标签到底是什么?
以训练集的第一个元素为例,我们尝试将它print出来,这用代码很容易实现
print('x_train[0]=\n{}\ny_train[0]={}'.format(x_train[0], y_train[0]))
结果是
x_train[0]=
[[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 3 18 18 18 126 136 175 26 166 255 247 127 0 0 0 0]
[ 0 0 0 0 0 0 0 0 30 36 94 154 170 253 253 253 253 253 225 172 253 242 195 64 0 0 0 0]
[ 0 0 0 0 0 0 0 49 238 253 253 253 253 253 253 253 253 251 93 82 82 56 39 0 0 0 0 0]
[ 0 0 0 0 0 0 0 18 219 253 253 253 253 253 198 182 247 241 0 0 0 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0 80 156 107 253 253 205 11 0 43 154 0 0 0 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0 0 14 1 154 253 90 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 139 253 190 2 0 0 0 0 0 0 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 11 190 253 70 0 0 0 0 0 0 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 35 241 225 160 108 1 0 0 0 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 81 240 253 253 119 25 0 0 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 45 186 253 253 150 27 0 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 16 93 252 253 187 0 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 249 253 249 64 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 46 130 183 253 253 207 2 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 39 148 229 253 253 253 250 182 0 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0 0 0 24 114 221 253 253 253 253 201 78 0 0 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0 23 66 213 253 253 253 253 198 81 2 0 0 0 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 18 171 219 253 253 253 253 195 80 9 0 0 0 0 0 0 0 0 0 0 0 0]
[ 0 0 0 0 55 172 226 253 253 253 253 244 133 11 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[ 0 0 0 0 136 253 253 253 212 135 132 16 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]]
y_train[0]=5
额,只看懂了它的标签是’5‘,我们不是cpu,看不懂这一堆数据是什么意思,但这么多数据对应了28*28个像素点的灰度值,我们可以show出来
plt.imshow(x_train[0], cmap='gray')
plt.show()
(2)搭建神经网络进行手写数字识别
认识MNIST数据集之后,我们就可以搭建一个基本的三层网络对手写数字进行分类识别,设置隐藏层神经元个数为128,使用relu,结合iris代码的复现,我们很容易就用python写出这个神经网络了
为了提升训练效果,我们可以在导入MNIST时对数据进行归一化处理
- 利用sequential
# import
import tensorflow as tf
# 导入dataset
mnist = tf.keras.datasets.mnist
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train, x_test = x_train / 255.0, x_test / 255.0
# model = models.Sequential
model = tf.keras.models.Sequential([
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(128, activation='relu'),
tf.keras.layers.Dense(10, activation='softmax')
])
# model.compile
model.compile(
optimizer='adam',
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=False),
metrics=['sparse_categorical_accuracy']
)
# model.fit
model.fit(
x_train, y_train,
batch_size=32, epochs=5,
validation_data=(x_test, y_test),
validation_freq=1
)
# model.summary
model.summary()
结果
Epoch 1/5
1875/1875 [==============================] - 3s 1ms/step - loss: 0.2566 - sparse_categorical_accuracy: 0.9262 - val_loss: 0.1357 - val_sparse_categorical_accuracy: 0.9588
Epoch 2/5
1875/1875 [==============================] - 2s 1ms/step - loss: 0.1150 - sparse_categorical_accuracy: 0.9658 - val_loss: 0.0966 - val_sparse_categorical_accuracy: 0.9710
Epoch 3/5
1875/1875 [==============================] - 2s 1ms/step - loss: 0.0795 - sparse_categorical_accuracy: 0.9757 - val_loss: 0.0892 - val_sparse_categorical_accuracy: 0.9732
Epoch 4/5
1875/1875 [==============================] - 2s 1ms/step - loss: 0.0600 - sparse_categorical_accuracy: 0.9816 - val_loss: 0.0786 - val_sparse_categorical_accuracy: 0.9753
Epoch 5/5
1875/1875 [==============================] - 3s 2ms/step - loss: 0.0455 - sparse_categorical_accuracy: 0.9862 - val_loss: 0.0839 - val_sparse_categorical_accuracy: 0.9744
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
flatten (Flatten) (None, 784) 0
dense (Dense) (None, 128) 100480
dense_1 (Dense) (None, 10) 1290
=================================================================
Total params: 101,770
Trainable params: 101,770
Non-trainable params: 0
_________________________________________________________________
注:这里每个epoch的1875指的是60000/32
- 利用class
# import
import tensorflow as tf
# 导入dataset
mnist = tf.keras.datasets.mnist
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train, x_test = x_train / 255.0, x_test / 255.0
# class model
class mnistModel(tf.keras.Model):
# 构建类
def __init__(self):
super(mnistModel, self).__init__()
# 定义网络结构块
self.inlayer = tf.keras.layers.Flatten()
self.hiddenlayer = tf.keras.layers.Dense(128, activation='relu')
self.outlayer = tf.keras.layers.Dense(10, activation='softmax')
def call(self, x):
# 调用网络结构块,实现前向传播
x = self.inlayer(x)
s1 = self.hiddenlayer(x)
y = self.outlayer(s1)
return y
model = mnistModel() # 实例化对象
# model.compile
model.compile(
optimizer='adam',
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=False),
metrics=['sparse_categorical_accuracy']
)
# model.fit
model.fit(
x_train, y_train,
batch_size=32, epochs=5,
validation_data=(x_test, y_test),
validation_freq=1
)
# model.summary
model.summary()
结果
Epoch 1/5
1875/1875 [==============================] - 3s 1ms/step - loss: 0.2608 - sparse_categorical_accuracy: 0.9261 - val_loss: 0.1376 - val_sparse_categorical_accuracy: 0.9606
Epoch 2/5
1875/1875 [==============================] - 3s 2ms/step - loss: 0.1171 - sparse_categorical_accuracy: 0.9656 - val_loss: 0.0935 - val_sparse_categorical_accuracy: 0.9725
Epoch 3/5
1875/1875 [==============================] - 4s 2ms/step - loss: 0.0802 - sparse_categorical_accuracy: 0.9758 - val_loss: 0.0857 - val_sparse_categorical_accuracy: 0.9726
Epoch 4/5
1875/1875 [==============================] - 4s 2ms/step - loss: 0.0603 - sparse_categorical_accuracy: 0.9820 - val_loss: 0.0809 - val_sparse_categorical_accuracy: 0.9753
Epoch 5/5
1875/1875 [==============================] - 3s 2ms/step - loss: 0.0451 - sparse_categorical_accuracy: 0.9858 - val_loss: 0.0770 - val_sparse_categorical_accuracy: 0.9769
Model: "mnist_model"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
flatten (Flatten) multiple 0
dense (Dense) multiple 100480
dense_1 (Dense) multiple 1290
=================================================================
Total params: 101,770
Trainable params: 101,770
Non-trainable params: 0
_________________________________________________________________
3. 练习:Fashion数据集及分类
(1)认识数据集
通过MNIST数据集,我们已经很熟悉认识这个新数据集的流程了
import tensorflow as tf
import matplotlib.pyplot as plt
# 导入dataset
fashion = tf.keras.datasets.fashion_mnist
(x_train, y_train), (x_test, y_test) = fashion.load_data()
# fashion数据集形状
print('x_train.shape:', x_train.shape)
print('y_train.shape', y_train.shape)
print('x_test.shape', x_test.shape)
print('y_test.shape', y_test.shape)
# 数据集内容
print('x_train[0]=\n{}\ny_train[0]={}'.format(x_train[0], y_train[0]))
plt.imshow(x_train[0], cmap='gray')
plt.show()
我们发现此数据集和MNIST数据集形状是相同的
x_train.shape: (60000, 28, 28)
y_train.shape (60000,)
x_test.shape (10000, 28, 28)
y_test.shape (10000,)
也就是说,Fashion也是由含60000个元素的训练集和含10000个元素的测试集组成的。对于每一个元素而言,对应的数据为一个2828(=784)大小的二维数组,对应的标签为一个11的数值
以训练集的第一个元素为例,我们将它print出来,结果是
x_train[0]=
[[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 13 73 0 0 1 4 0 0 0 0 1 1 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 3 0 36 136 127 62 54 0 0 0 1 3 4 0 0 3]
[ 0 0 0 0 0 0 0 0 0 0 0 0 6 0 102 204 176 134 144 123 23 0 0 0 0 12 10 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 155 236 207 178 107 156 161 109 64 23 77 130 72 15]
[ 0 0 0 0 0 0 0 0 0 0 0 1 0 69 207 223 218 216 216 163 127 121 122 146 141 88 172 66]
[ 0 0 0 0 0 0 0 0 0 1 1 1 0 200 232 232 233 229 223 223 215 213 164 127 123 196 229 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 183 225 216 223 228 235 227 224 222 224 221 223 245 173 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 193 228 218 213 198 180 212 210 211 213 223 220 243 202 0]
[ 0 0 0 0 0 0 0 0 0 1 3 0 12 219 220 212 218 192 169 227 208 218 224 212 226 197 209 52]
[ 0 0 0 0 0 0 0 0 0 0 6 0 99 244 222 220 218 203 198 221 215 213 222 220 245 119 167 56]
[ 0 0 0 0 0 0 0 0 0 4 0 0 55 236 228 230 228 240 232 213 218 223 234 217 217 209 92 0]
[ 0 0 1 4 6 7 2 0 0 0 0 0 237 226 217 223 222 219 222 221 216 223 229 215 218 255 77 0]
[ 0 3 0 0 0 0 0 0 0 62 145 204 228 207 213 221 218 208 211 218 224 223 219 215 224 244 159 0]
[ 0 0 0 0 18 44 82 107 189 228 220 222 217 226 200 205 211 230 224 234 176 188 250 248 233 238 215 0]
[ 0 57 187 208 224 221 224 208 204 214 208 209 200 159 245 193 206 223 255 255 221 234 221 211 220 232 246 0]
[ 3 202 228 224 221 211 211 214 205 205 205 220 240 80 150 255 229 221 188 154 191 210 204 209 222 228 225 0]
[ 98 233 198 210 222 229 229 234 249 220 194 215 217 241 65 73 106 117 168 219 221 215 217 223 223 224 229 29]
[ 75 204 212 204 193 205 211 225 216 185 197 206 198 213 240 195 227 245 239 223 218 212 209 222 220 221 230 67]
[ 48 203 183 194 213 197 185 190 194 192 202 214 219 221 220 236 225 216 199 206 186 181 177 172 181 205 206 115]
[ 0 122 219 193 179 171 183 196 204 210 213 207 211 210 200 196 194 191 195 191 198 192 176 156 167 177 210 92]
[ 0 0 74 189 212 191 175 172 175 181 185 188 189 188 193 198 204 209 210 210 211 188 188 194 192 216 170 0]
[ 2 0 0 0 66 200 222 237 239 242 246 243 244 221 220 193 191 179 182 182 181 176 166 168 99 58 0 0]
[ 0 0 0 0 0 0 0 40 61 44 72 41 35 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]]
y_train[0]=9
鞋子对应的标签为‘9’,通过查阅资料:该数据集用0-9分别表示10种不同的衣物
(2)搭建神经网络训练
# import
import tensorflow as tf
# 导入dataset
fashion = tf.keras.datasets.fashion_mnist
(x_train, y_train), (x_test, y_test) = fashion.load_data()
x_train, x_test = x_train / 255.0, x_test / 255.0
# model = models.Sequential
model = tf.keras.models.Sequential([
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(512, activation='relu'),
tf.keras.layers.Dense(512, activation='relu'),
tf.keras.layers.Dense(10, activation='softmax')
])
''''也可以使用如下方法
# class model
class fashionModel(tf.keras.Model):
# 构建类
def __init__(self):
super(fashionModel, self).__init__()
# 定义网络结构块
self.inlayer = tf.keras.layers.Flatten()
self.hiddenlayer = tf.keras.layers.Dense(256, activation='relu')
self.hiddenlayer = tf.keras.layers.Dense(256, activation='relu')
self.outlayer = tf.keras.layers.Dense(10, activation='softmax')
def call(self, x):
# 调用网络结构块,实现前向传播
x = self.inlayer(x)
s1 = self.hiddenlayer(x)
y = self.outlayer(s1)
return y
model = fashionModel() # 实例化对象'''
# model.compile
model.compile(
optimizer='adam',
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=False),
metrics=['sparse_categorical_accuracy']
)
# model.fit
model.fit(
x_train, y_train,
batch_size=32, epochs=5,
validation_data=(x_test, y_test),
validation_freq=1
)
# model.summary
model.summary()
结果(我尝试了更改隐藏层的层数和神经元个数,在相同epoch的情况下似乎没有什么显著的改变)
Epoch 1/5
1875/1875 [==============================] - 22s 11ms/step - loss: 0.4655 - sparse_categorical_accuracy: 0.8287 - val_loss: 0.4106 - val_sparse_categorical_accuracy: 0.8519
Epoch 2/5
1875/1875 [==============================] - 22s 12ms/step - loss: 0.3535 - sparse_categorical_accuracy: 0.8697 - val_loss: 0.3885 - val_sparse_categorical_accuracy: 0.8632
Epoch 3/5
1875/1875 [==============================] - 21s 11ms/step - loss: 0.3178 - sparse_categorical_accuracy: 0.8829 - val_loss: 0.3430 - val_sparse_categorical_accuracy: 0.8770
Epoch 4/5
1875/1875 [==============================] - 18s 10ms/step - loss: 0.2954 - sparse_categorical_accuracy: 0.8898 - val_loss: 0.3423 - val_sparse_categorical_accuracy: 0.8769
Epoch 5/5
1875/1875 [==============================] - 16s 9ms/step - loss: 0.2769 - sparse_categorical_accuracy: 0.8951 - val_loss: 0.3506 - val_sparse_categorical_accuracy: 0.8777
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
flatten (Flatten) (None, 784) 0
dense (Dense) (None, 512) 401920
dense_1 (Dense) (None, 512) 262656
dense_2 (Dense) (None, 10) 5130
=================================================================
Total params: 669,706
Trainable params: 669,706
Non-trainable params: 0
_________________________________________________________________
三、网络八股功能扩展
复盘六步法
(1)总结
- import
- train, test
- model = Sequential / Class
- model.compile
- model.fit
- model.summary
(2)限制
- 导入数据都是load_data调库,如果是自己专业领域数据怎么办?——自制数据集
- 数据量少,模型泛化能力弱?——数据增强
- 每次模型训练从零开始?——断点续训,实时保存最优模型
- 保存训练好的参数?——参数提取
- 训练/测试效果?——Acc/Loss可视化
- 学到的知识如何在实际中应用?——给图识物应用程序(将在第四部分介绍)
基于上述限制,将以MNIST数据集训练网络代码为模板进行修改,并一一给出解决方案
1. 自制数据集
库中的数据集虽然好用,但只能作为一个范例,当我们想要以专业领域的数据集进行训练时,自制数据集是必要的
功能代码实现
从以文件形式存储的数据到能够作为训练依据的数据集,主要过程是读取文件内容、对内容进行规范化处理、写入内存等,为方便起见,我编写了一个类,包含对MNIST数据集和Fashion数据集的生成,可以看出,基本就是对文件的操作以及一些规范化
class SelfMadeDataset():
def __init__(self):
pass
def generateds(self, path, txt_path):
f = open(txt_path, 'r')
# 逐行读出,每一行格式为“图片地址 标签”,如“28755_0.jpg 0”
contents = f.readlines()
f.close()
x, y = [], [] # x, y分别存放数据和标签
for content in contents:
value = content.split() # 每一行以空格分开,value = [图片地址, 标签]
img_path = path + value[0] # 总路径+该图片路径
img = Image.open(img_path)
img = np.array(img.convert('L')) # 标准化
img = img / 255. # 归一化
x.append(img)
y.append(value[1])
print('loading:'+content) # print出加载进程
x = np.array(x)
y = np.array(y)
y = y.astype(np.int64)
return x, y
def load_mnist(self):
# 一级目录地址
dic_path = "D:/source/repos/FNN/MNIST_FC/mnist_image_label/"
# 相关文件夹及txt文件的偏移地址
train_path = dic_path + 'mnist_train_jpg_60000/'
train_txt = dic_path + 'mnist_train_jpg_60000.txt'
x_train_savepath = dic_path + 'mnist_x_train.npy'
y_train_savepath = dic_path + 'mnist_y_train.npy'
test_path = dic_path + 'mnist_test_jpg_10000/'
test_txt = dic_path + 'mnist_test_jpg_10000.txt'
x_test_savepath = dic_path + 'mnist_x_test.npy'
y_test_savepath = dic_path + 'mnist_y_test.npy'
# 如果.npy文件已经创建完成
if os.path.exists(x_train_savepath) and \
os.path.exists(y_train_savepath) and \
os.path.exists(x_test_savepath) and \
os.path.exists(y_test_savepath):
# img和label信息通过若干个一维数组存放,需要对img形状进行重塑,并分别存入x/y中
print('---------- Load Datasets ----------')
x_train_save = np.load(x_train_savepath)
x_train = np.reshape(x_train_save, (len(x_train_save), 28, 28))
y_train = np.load(y_train_savepath)
x_test_save = np.load(x_test_savepath)
x_test = np.reshape(x_test_save, (len(x_test_save), 28, 28))
y_test = np.load(y_test_savepath)
else:
# 先直接将数据和标签存入输出
print('---------- Generate Datasets ----------')
x_train, y_train = self.generateds(train_path, train_txt)
x_test, y_test = self.generateds(test_path, test_txt)
# 再以若干行(一维数组)的形式存入.txt文件中
print('---------- Save Datasets ----------')
x_train_save = np.reshape(x_train, (len(x_train), -1))
x_test_save = np.reshape(x_test, (len(x_test), -1))
np.save(x_train_savepath, x_train_save)
np.save(y_train_savepath, y_train)
np.save(x_test_savepath, x_test_save)
np.save(y_test_savepath, y_test)
return (x_train, y_train), (x_test, y_test)
# 类似可以写出Fashion自制数据集
def load_fashion(self):
# 一级目录地址
dic_path = "D:/source/repos/FNN/FASHION_FC/fashion_image_label/"
train_path = dic_path + 'fashion_train_jpg_60000/'
train_txt = dic_path + 'fashion_train_jpg_60000.txt'
x_train_savepath = dic_path + 'fashion_x_train.npy'
y_train_savepath = dic_path + 'fashion_y_train.npy'
test_path = dic_path + 'fashion_test_jpg_10000/'
test_txt = dic_path + 'fashion_test_jpg_10000.txt'
x_test_savepath = dic_path + 'fashion_x_test.npy'
y_test_savepath = dic_path + 'fashion_y_test.npy'
if os.path.exists(x_train_savepath) and \
os.path.exists(y_train_savepath) and \
os.path.exists(x_test_savepath) and \
os.path.exists(y_test_savepath):
print('---------- Load Datasets ----------')
x_train_save = np.load(x_train_savepath)
x_train = np.reshape(x_train_save, (len(x_train_save), 28, 28))
y_train = np.load(y_train_savepath)
x_test_save = np.load(x_test_savepath)
x_test = np.reshape(x_test_save, (len(x_test_save), 28, 28))
y_test = np.load(y_test_savepath)
else:
print('---------- Generate Datasets ----------')
x_train, y_train = self.generateds(train_path, train_txt)
x_test, y_test = self.generateds(test_path, test_txt)
print('---------- Save Datasets ----------')
x_train_save = np.reshape(x_train, (len(x_train), -1))
x_test_save = np.reshape(x_test, (len(x_test), -1))
np.save(x_train_savepath, x_train_save)
np.save(y_train_savepath, y_train)
np.save(x_test_savepath, x_test_save)
np.save(y_test_savepath, y_test)
return (x_train, y_train), (x_test, y_test)
八股修改
以MNIST数据集为例,我们仅需要将原来第二部分的
# 导入dataset
mnist = tf.keras.datasets.mnist
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train, x_test = x_train / 255.0, x_test / 255.0
更改为
# 导入dataset
mnist = expand.SelfMadeDataset()
(x_train, y_train), (x_test, y_test) = mnist.load_fashion()
注:因我们的自制数据集已经将数据规范化,因此不用再进行规范化操作了
2. 数据增强
给定的数据集并不能完全反应真实情况,同时有时数据集元素的数量较少、情况较为单一,因此训练出的模型泛化能力不一定强,因此,利用进行伸缩、旋转、翻转等变换后的图像进行训练是十分必要的,这就是所谓的数据增强
核心函数
首先实例化数据增强类
image_gen_train = tf.keras.preprocessing.image.ImageDataGenerator(...)
这个函数有以下几个参数:
rescale=所有数据将乘以该数值(可归一化)rotation_range=随机旋转角度数范围width_shift_range=随机宽度偏移量height_shift_range=随机高度偏移量horizontal_flip=是否随机水平翻转zoom_range=随机缩放的范围(1±x)
之后,对类进行操作用以对训练集进行数据增强,并在model.fit训练时匹配,注意这里的x_train要求为四维数组,因此需要进行reshape
image_gen_train.fit(x_train)model.fit(image_gen_train.flow(x_train, y_train, batch_size=32), ...)
相关代码
依据上述核心函数,在MNIST原代码上调整,得到(省略号部分和原先保持一致)
# import
...
# 导入dataset
...
# data_gen
x_train = x_train.reshape(x_train.shape[0], 28, 28, 1)
image_gen_train = tf.keras.preprocessing.image.ImageDataGenerator(
rescale=1. / 1.,
rotation_range=45,
width_shift_range=.15,
height_shift_range=.15,
horizontal_flip=False,
zoom_range=0.5
)
image_gen_train.fit(x_train)
# model = models.Sequential
...
# model.compile
...
# model.fit
model.fit(
image_gen_train.flow(x_train, y_train, batch_size=32), # 同步更新
epochs=5,
validation_data=(x_test, y_test),
validation_freq=1
)
# model.summary
...
结果说明
最终测试集准确率大概达到了0.92,和数据增强前(0.97)比较甚至变低了,但这并不能反映数据增强的真实效果,因为我们的测试集是标准的MNIST数据集,而不是实际情况,而在实际的手写数据识别中,数据增强的意义就体现出来了
3. 断点续训
每次训练都从零开始显然是费时费力的,为了解决这个问题,我们是否可以保存训练好的参数呢?这便是所谓的断点续训的方法,每次训练结束后可根据需要将训练好的相关量保存在本地,方便后续调用
代码实现
在训练前,加入断点内容保存和回调函数代码
# checkpoint save & callback
checkpoint_save_path = "./checkpoint/mnist.ckpt"
if os.path.exists(checkpoint_save_path + '.index'):
print('---------- Load the Model ----------')
model.load_weights(checkpoint_save_path)
cp_callback = tf.keras.callbacks.ModelCheckpoint(
filepath=checkpoint_save_path,
save_weights_only=True,
save_best_only=True
)
训练时,加入参数
callbacks=[cp_callback]
使用效果
若从零开始,慢慢向上爬
Epoch 1/5
val_loss: 0.1375 - val_sparse_categorical_accuracy: 0.9585
Epoch 2/5
val_loss: 0.1008 - val_sparse_categorical_accuracy: 0.9680
Epoch 3/5
val_loss: 0.0843 - val_sparse_categorical_accuracy: 0.9728
Epoch 4/5
val_loss: 0.0774 - val_sparse_categorical_accuracy: 0.9766
Epoch 5/5
val_loss: 0.0732 - val_sparse_categorical_accuracy: 0.9763
使用之前的结果,“出生即巅峰”
---------- Load the Model ----------
Epoch 1/5
val_loss: 0.0797 - val_sparse_categorical_accuracy: 0.9752
Epoch 2/5
val_loss: 0.0809 - val_sparse_categorical_accuracy: 0.9776
Epoch 3/5
val_loss: 0.0871 - val_sparse_categorical_accuracy: 0.9750
Epoch 4/5
val_loss: 0.0760 - val_sparse_categorical_accuracy: 0.9786
Epoch 5/5
val_loss: 0.0812 - val_sparse_categorical_accuracy: 0.9772
4. 参数提取
断点续训保留了每次训练后的最优参数,那么如何查看这些参数值呢?这便是参数提取的内容了
直接查看
一个很自然的想法是print出来,一行代码就搞定了
print(model.trainable_variables)
看看结果(这里只复制了第一个参数)
[<tf.Variable 'dense/kernel:0' shape=(784, 128) dtype=float32, numpy=
array([[ 0.00500327, 0.04753769, -0.01752532, ..., 0.03947137,
-0.01869851, -0.06784071],
[ 0.03976591, -0.01105286, -0.06868242, ..., -0.02361085,
-0.01682989, -0.01024982],
[ 0.06888347, -0.08000371, 0.04266344, ..., -0.01104672,
-0.05294819, -0.05270603],
...,
[ 0.03220175, 0.05865171, -0.06073547, ..., 0.03521375,
0.04109269, 0.061808 ],
[-0.00427113, -0.02391875, 0.0570228 , ..., 0.01772309,
-0.01797158, 0.03190365],
[-0.06256977, -0.06899459, -0.02244005, ..., 0.02622585,
0.05694849, 0.05649317]]
每个结果中间都有省略号,这是因为数据太多了,而想要查看完整的参数,只需在最开始加入一行代码
np.set_printoptions(threshold=np.inf)
threshold这个值表示限制到多少,可以任意更改;这次的结果便是不带省略号的完整版(太多了就不复制了)
保存本地
如果想在本地查看参数值,可以以.txt文件记录到本地
# save to disk
file = open('./weights.txt', 'w')
for v in model.trainable_variables:
file.write(str(v.name) + '\n')
file.write(str(v.shape) + '\n')
file.write(str(v.numpy()) + '\n')
file.close()
5. Acc/Loss可视化
同样,我们想要以更加直观的方式查看训练/测试效果
代码实现
加val的表示validation(验证集/测试集)
# visualize acc & loss
acc = history.history['sparse_categorical_accuracy']
val_acc = history.history['val_sparse_categorical_accuracy']
loss = history.history['loss']
val_loss = history.history['val_loss']
plt.subplot(1, 2, 1)
plt.plot(acc, label='Training Accuracy')
plt.plot(val_acc, label='Validation Accuracy')
plt.title('Training and Validation Accuracy')
plt.legend()
plt.subplot(1, 2, 2)
plt.plot(loss, label='Training Loss')
plt.plot(val_loss, label='Validation Loss')
plt.title('Training and Validation Loss')
plt.legend()
plt.suptitle('Curves of Accuracy and Loss')
# plt.savefig('./results.png') # save to disk
plt.show()
结果展示
四、从训练到实际
经过了不断的改进和训练,我们得到了越加完美的参数空间,我们可以通过这些参数来进行真正的手写数字识别
训练源码
# import
import matplotlib.pyplot as plt
import tensorflow as tf
import numpy as np
import os
np.set_printoptions(threshold=np.inf)
# 导入dataset
mnist = tf.keras.datasets.mnist
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train, x_test = x_train / 255.0, x_test / 255.0
# data_gen
x_train = x_train.reshape(x_train.shape[0], 28, 28, 1)
image_gen_train = tf.keras.preprocessing.image.ImageDataGenerator(
rescale=1. / 1.,
rotation_range=45,
width_shift_range=.15,
height_shift_range=.15,
horizontal_flip=False,
zoom_range=0.5
)
image_gen_train.fit(x_train)
# model = models.Sequential
model = tf.keras.models.Sequential([
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(128, activation='relu'),
tf.keras.layers.Dense(10, activation='softmax')
])
# model.compile
model.compile(
optimizer='adam',
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=False),
metrics=['sparse_categorical_accuracy']
)
# checkpoint save & callback
checkpoint_save_path = "./checkpoint/mnist.ckpt"
if os.path.exists(checkpoint_save_path + '.index'):
print('---------- Load the Model ----------')
model.load_weights(checkpoint_save_path)
cp_callback = tf.keras.callbacks.ModelCheckpoint(
filepath=checkpoint_save_path,
save_weights_only=True,
save_best_only=True
)
# model.fit
history = model.fit(
image_gen_train.flow(x_train, y_train, batch_size=32), epochs=5,
validation_data=(x_test, y_test),
validation_freq=1,
callbacks=[cp_callback]
)
# model.summary
model.summary()
# save to disk
file = open('./weights.txt', 'w')
for v in model.trainable_variables:
file.write(str(v.name) + '\n')
file.write(str(v.shape) + '\n')
file.write(str(v.numpy()) + '\n')
file.close()
''''# visualize acc & loss
acc = history.history['sparse_categorical_accuracy']
val_acc = history.history['val_sparse_categorical_accuracy']
loss = history.history['loss']
val_loss = history.history['val_loss']
plt.subplot(1, 2, 1)
plt.plot(acc, label='Training Accuracy')
plt.plot(val_acc, label='Validation Accuracy')
plt.title('Training and Validation Accuracy')
plt.legend()
plt.subplot(1, 2, 2)
plt.plot(loss, label='Training Loss')
plt.plot(val_loss, label='Validation Loss')
plt.title('Training and Validation Loss')
plt.legend()
plt.suptitle('Curves of Accuracy and Loss')
# plt.savefig('./results.png') # save to disk
plt.show()'''
''''# class model
class mnistModel(tf.keras.Model):
# 构建类
def __init__(self):
super(mnistModel, self).__init__()
# 定义网络结构块
self.inlayer = tf.keras.layers.Flatten()
self.hiddenlayer = tf.keras.layers.Dense(128, activation='relu')
self.outlayer = tf.keras.layers.Dense(10, activation='softmax')
def call(self, x):
# 调用网络结构块,实现前向传播
x = self.inlayer(x)
s1 = self.hiddenlayer(x)
y = self.outlayer(s1)
return y
model = mnistModel() # 实例化对象'''
应用源码
import cv2 as cv
import numpy as np
from PIL import Image
import tensorflow as tf
def recognition():
model_save_path = "./checkpoint/mnist.ckpt"
# model = models.Sequential
model = tf.keras.models.Sequential([
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(128, activation='relu'),
tf.keras.layers.Dense(10, activation='softmax')
])
model.load_weights(model_save_path)
image_path = './MNIST_FC/number.png'
img = Image.open(image_path)
img = img.resize((28, 28), Image.ANTIALIAS)
img_arr = np.array(img.convert('L'))
# 图像预处理,滤去噪声
for m in range(28):
for n in range(28):
if img_arr[m][n] < 200:
img_arr[m][n] = 255
else:
img_arr[m][n] = 0
img_arr = img_arr / 255.
x_predict = img_arr[tf.newaxis, ...]
print('---------- Recognizing ----------')
result = model.predict(x_predict)
pred = tf.argmax(result, axis=1)
result = str(pred[0].numpy())
print('---------- Success! ----------')
print('\nthe number is:{}'.format(result))
return result
# 鼠标的回调函数的参数格式是固定的,不要随意更改。
def mouse_event(event, x, y, flags, param):
global start, drawing
# 左键按下:开始画图
if event == cv.EVENT_LBUTTONDOWN:
drawing = True
start = (x, y)
# 鼠标移动,画图
elif event == cv.EVENT_MOUSEMOVE:
if drawing:
cv.circle(img, (x, y), 8, 0, -1)
# 左键释放:结束画图
elif event == cv.EVENT_LBUTTONUP:
drawing = False
cv.circle(img, (x, y), 8, 0, -1)
def initialize():
cv.destroyAllWindows() # 清空所有窗口
img = 255 * np.ones((256, 256), np.uint8) # 创建白幕
cv.namedWindow('image')
cv.setMouseCallback('image', mouse_event)
return img
def show():
if flag:
src = cv.imread('./MNIST_FC/number.png')
# 调用cv.putText()添加文字
text = recognition()
AddText = src.copy()
cv.putText(AddText, text, (0, 50), cv.FONT_HERSHEY_COMPLEX, 1.5, (0, 0, 255), 5)
# 显示拼接后的图片
cv.imshow('text', AddText)
cv.waitKey()
img = initialize()
return img
drawing = False # 是否开始画图
start = (-1, -1)
flag = False
img = initialize()
while True:
cv.imshow('image', img)
# 按ESC键退出程序
if cv.waitKey(1) == 27:
break
# 按r重启
elif cv.waitKey(1) == ord('r'):
img = initialize()
continue
# 按Enter进行识别
elif cv.waitKey(1) == 13:
flag = True
cv.imwrite('./MNIST_FC/number.png', img)
show()
continue
opencv与手写板部分,参考了这位大神的文章,cv2库就是opencv,可以直接安装
pip install opencv-python
使用效果
还是蛮好玩的,就是有点出墨不太顺畅and很卡,以及‘4’容易识别成‘9’,正确率在可接受范围内吧,今后还可以继续改进!
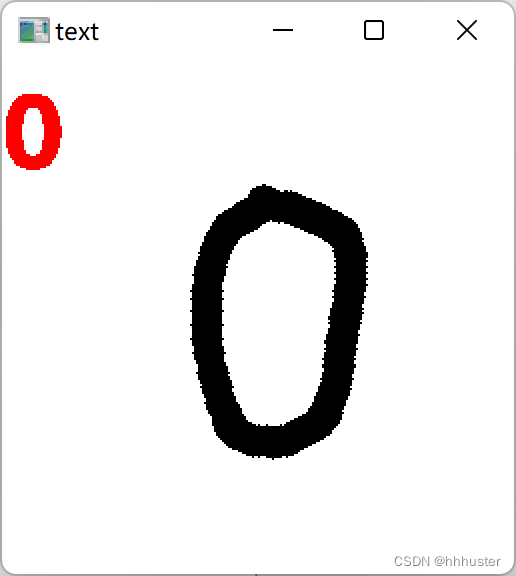

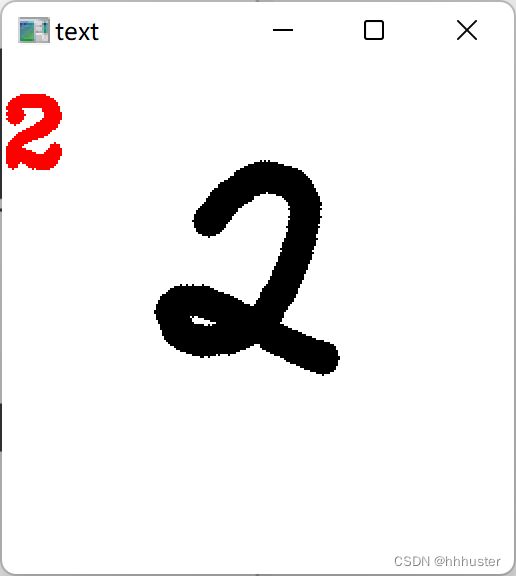



这一部分名字是“八股”,内容还是很多的,尤其是我把老师两讲的东西合到了一起,不过给我的感觉就是很大一部分都是在“套模板”,不是很难,没什么可以发挥的地方。不过在此过程中,也了解到了关于文件、cv等“附加内容”,也还是蛮有收获的吧,ok收工啦!






