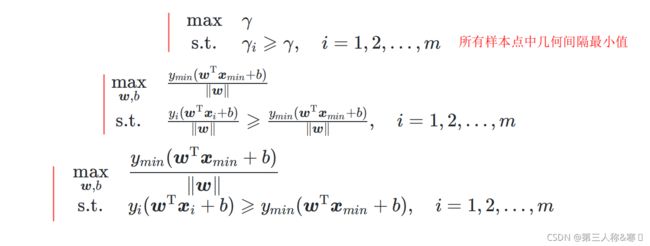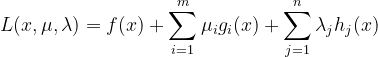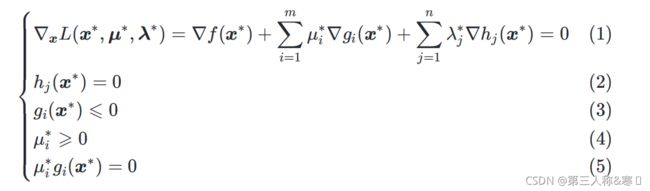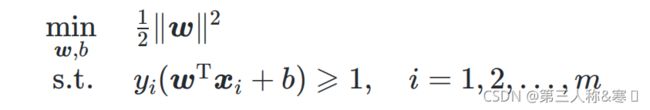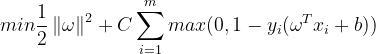机器学习-支持向量机
目录
前言
一、间隔与支持向量
1.1超平面
1.2几何间隔
二、支持向量机(SVM)
2.1 支持向量机模型
2.2 策略——最优化目标函数
2.3算法——拉格朗日对偶法
三、软间隔与支持向量回归
3.1算法原理
3.2软间隔
3.3支持向量回归(SVR)
总结
前言
本文主要记录了有关机器学习问题中支持向量机的部分,思路均来源于周志华老师《机器学习》第六章的内容和谢文睿老师的《机器学习公式详解》。
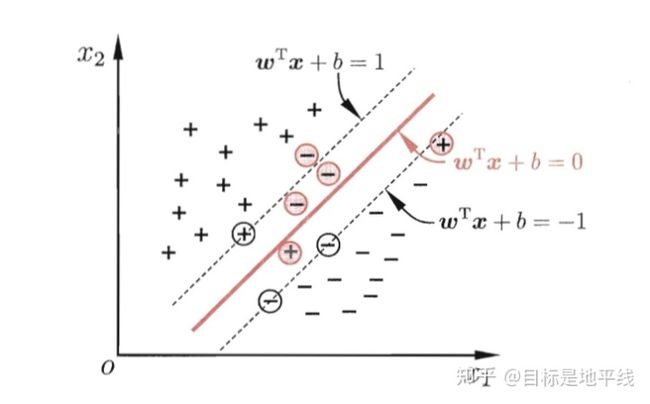
一、间隔与支持向量
对于给定的训练样本集![]() ,
,![]() ,分类学习基本想法就是基于训练集
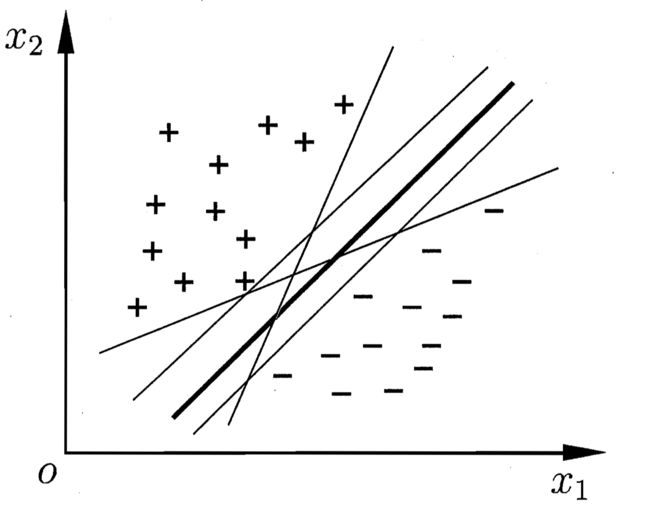
,分类学习基本想法就是基于训练集![]() 在样本空间找到一个划分超平面,将不同类别的样本分开。
在样本空间找到一个划分超平面,将不同类别的样本分开。
但可以看出,在上图中,位于“正中间的划分超平面”受到训练集的局限性或噪声因素的影响比较小,即鲁棒性最好、对未见示例的泛化能力最强。
1.1超平面
在样本空间中,划分超平面可以通过如下线性方程描述:![]() ,其中
,其中![]() 为法向量,决定了超平面的方向;
为法向量,决定了超平面的方向;![]() 为位移项,决定了超平面与原点之间的距离。样本空间中的任意点
为位移项,决定了超平面与原点之间的距离。样本空间中的任意点![]() ,其到超平面的距离可以写为
,其到超平面的距离可以写为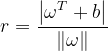 。
。
以下给出证明过程:
1.2几何间隔
对于给定的数据集![]() 和超平面
和超平面![]() ,定义数据集中任意一个样本点
,定义数据集中任意一个样本点![]() ,
,![]() ,
,![]() ,关于超平面的几何间隔为
,关于超平面的几何间隔为![]() 。
。
正确分类时:![]() ,几何间隔等价于点到超平面的距离;
,几何间隔等价于点到超平面的距离;
未正确分类时:![]() 。
。
对于给定数据集![]() 和超平面
和超平面![]() ,定义此数据集关于超平面的几何间隔为:数据集
,定义此数据集关于超平面的几何间隔为:数据集![]() 中所有样本点的几何间隔最小值。
中所有样本点的几何间隔最小值。![]() ,
,![]() 。
。
二、支持向量机(SVM)
2.1 支持向量机模型
模型:对于给定线性可分的数据集![]() ,支持向量机模型希望求得数据集
,支持向量机模型希望求得数据集![]() 关于超平面的几何间隔
关于超平面的几何间隔![]() 达到最大的那个超平面,再加上一个
达到最大的那个超平面,再加上一个![]() 函数实现分类功能:
函数实现分类功能:
![]()
本质上,和感知机相同,仍然在于求这样一个超平面,而几何间隔最大的超平面就是“距离正负样本最远的超平面”,原因在于:
- 当超平面没有正确划分正负样本时:几何间隔最小的为误分点,此时
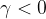 ;
; - 当超平面正确划分正负样本时,
 ,且越靠近中央
,且越靠近中央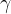 越大。
越大。
2.2 策略——最优化目标函数
策略:给定线性可分数据集![]() ,设
,设![]() 中几何间隔最小的样本为
中几何间隔最小的样本为![]() ,那么支持向量机找超平面的过程可以转化为以下带约束条件的优化问题:
,那么支持向量机找超平面的过程可以转化为以下带约束条件的优化问题:
假设该问题的最优解为![]() ,那么
,那么![]() ,
,![]() 也是最优解,且对应的超平面不改变,因此若想让上述优化问题有可解的唯一解,需要做一定的限制。
也是最优解,且对应的超平面不改变,因此若想让上述优化问题有可解的唯一解,需要做一定的限制。
令![]() ,因为对于特定的
,因为对于特定的![]() 来说,能够满足此式的
来说,能够满足此式的![]() 有且仅有一个,对应的最优解也只有一对,故将上述优化问题转化为:
有且仅有一个,对应的最优解也只有一对,故将上述优化问题转化为:
此优化问题为含不等式约束的优化问题,且为凸优化问题,故可以用很多求解凸优化问题的方法求解该问题。这里采用拉格朗日对偶来求解。
为什么支持向量机是一个凸优化问题?
2.3算法——拉格朗日对偶法
对于一般地约束优化问题(不一定是凸优化问题):
![]()
![]()
![]()
设上述优化问题的定义域为![]() =
=![]() 、
、![]() 、
、![]() 定义域的交集,可行集(满足定义域的基础上满足限制条件)为:
定义域的交集,可行集(满足定义域的基础上满足限制条件)为:![]() ,最优值为
,最优值为![]() 。
。
由拉格朗日函数定义可知,上述优化问题的拉格朗日函数为:
其中![]() ,
,![]() 为不等式、等式约束条件的拉格朗日乘子向量。
为不等式、等式约束条件的拉格朗日乘子向量。
定义:上述优化问题的拉格朗日对偶函数![]() ,为
,为![]() 关于
关于![]() 的下确界(下限),也即
的下确界(下限),也即
对偶函数![]() 有如下重要性质:
有如下重要性质:
- 无论上述优化问题是否为凸优化问题,其对偶函数
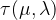 一定为凹函数;
一定为凹函数; - 当
 时,
时,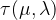 构成了上述优化问题最优解
构成了上述优化问题最优解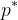 的下界,即
的下界,即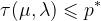 成立。
成立。
为什么
成立?
定义:在![]() 的约束条件下,“求对偶函数最大值的优化问题”为“拉格朗日对偶问题”。(原优化问题为主问题)
的约束条件下,“求对偶函数最大值的优化问题”为“拉格朗日对偶问题”。(原优化问题为主问题)
![]()
![]() ,
,![]()
设该优化问题的最优解为![]() ,则有
,则有![]() ,对应为“弱对偶”成立,若
,对应为“弱对偶”成立,若![]() ,对应为“强对偶”成立。找到了间接求
,对应为“强对偶”成立。找到了间接求![]() 的方法!
的方法!
结论:设![]() 、
、![]() 、
、![]() 一阶偏导连续,
一阶偏导连续,![]() 分别为主问题和对偶问题的最优解,若强对偶性成立,则
分别为主问题和对偶问题的最优解,若强对偶性成立,则![]() 满足以下5个
满足以下5个![]() 条件:
条件:
为什么支持向量机问题常常采用拉格朗日对偶求解?
),而对偶问题和数据量成正比(因为未知量是
),当特
征维数远高于数据量的时候拉格朗日对偶更高效;
三、软间隔与支持向量回归
3.1算法原理
以上讨论过程中,我们一直假定训练样本在样本空间或特征空间可分,即存在一个超平面能将不同类的样本完全划分开。而现实任务中,线性不可分的情形才是最常见的,因此需要允许支持向量机犯错,为此引入“软间隔”的概念。
从数学角度来看,软间隔即为允许(但尽可能少)部分样本不满足以下约束条件:
必须严格执行的约束条件![]() 具有一定灵活性的损失
具有一定灵活性的损失
合格的损失函数满足以下要求,才能保证在最小化损失时,保证不满足约束条件的样本尽可能少:
3.2软间隔
由以上原则,软间隔的优化目标(策略)可以写为:
其中,![]() 是一个常数,用于调节损失的权重,当
是一个常数,用于调节损失的权重,当![]() 时,会迫使所有样本的损失为0,进而退化为严格执行的约束条件,即“硬间隔”。因此,此时可视为支持向量机的一般化形式。
时,会迫使所有样本的损失为0,进而退化为严格执行的约束条件,即“硬间隔”。因此,此时可视为支持向量机的一般化形式。
由于![]() 非凸、非连续,数学性质不好,是优化目标不易求解,故常用“替代损失函数”来替代
非凸、非连续,数学性质不好,是优化目标不易求解,故常用“替代损失函数”来替代![]() ,软间隔支持向量机常采用
,软间隔支持向量机常采用![]() (合页)损失:
(合页)损失:
![]() ;
;
对应即为常用的“软间隔支持向量机”,仍然是一个二次规划问题,可以用拉格朗日乘子法求解满足的参数条件。
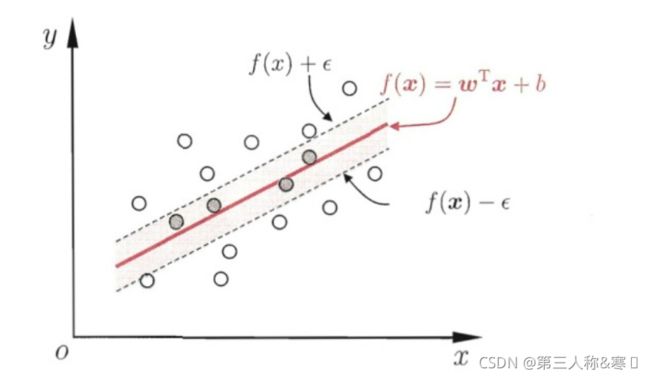
3.3支持向量回归(SVR)
根本思路:落在带子上的样本不计算损失(类比线性回归在线上的点预测误差为0),不在带子上的则以偏离带子的距离作为损失(类比线性回归的均方误差),然后以最小化损失的方式迫使间隔带从样本最密集的地方(中心地带)穿过,进而达到拟合训练样本的目的。
其中![]() 为
为![]() 的正则项,此处引入正则项除了起正则化本身的作用外,也是为了和支持向量机的优化目标保持形式上的一致,这样可以导出对偶函数引入核函数,
的正则项,此处引入正则项除了起正则化本身的作用外,也是为了和支持向量机的优化目标保持形式上的一致,这样可以导出对偶函数引入核函数,![]() 为调节损失权重的常数。
为调节损失权重的常数。
故![]() 的优化问题可以改写为:
的优化问题可以改写为:
由此转化为了类似于支持向量机的类型,解参方法相似。
总结
以上思路均来源于《机器学习》这本书第六章的内容。仅代表个人的思路和理解,如有错误欢迎指正!