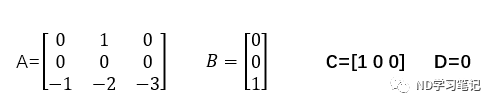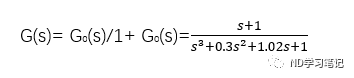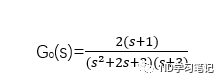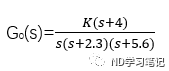一阶系统开环传递函数表达式_simulink控制系统仿真之控制系统的分析方法(1)(时域分析法+根轨迹法)...
控制系统的传统分析方法有时域分析法、根轨迹分析法、频域分析法,它们属于经典控制理论的范畴。状态空间分析法能揭示系统内部变量和外部变量之间的关系,因而有可能找出系统中未被认识的许多重要特性,它比经典控制理论更为全面。 下面对上述几种方法进行介绍。 1.时域分析法 时域分析法以拉氏变换为工具,从传递函数触发,直接从时间域上对控制系统性能进行研究。主要用于分析系统的动态性能,是其他分析方法的基础。 时域响应
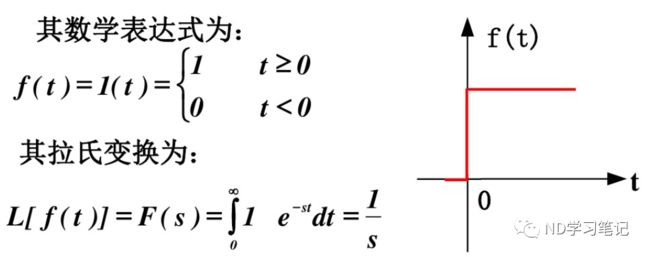 可如前例使用step函数仿真 3.单位斜坡响应
可如前例使用step函数仿真 3.单位斜坡响应  4.单位加速度坡 响应
4.单位加速度坡 响应 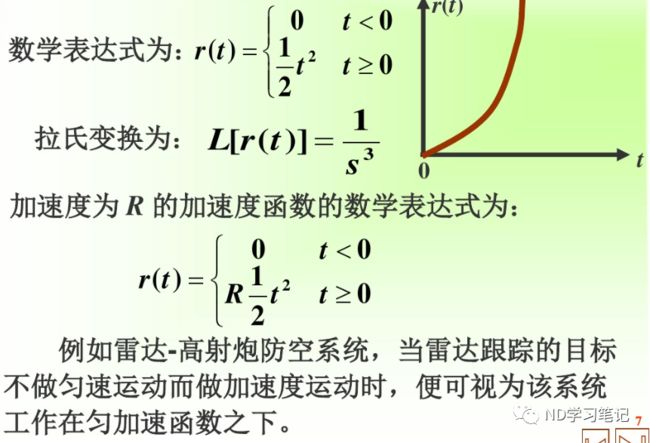 5.单位正弦 响应
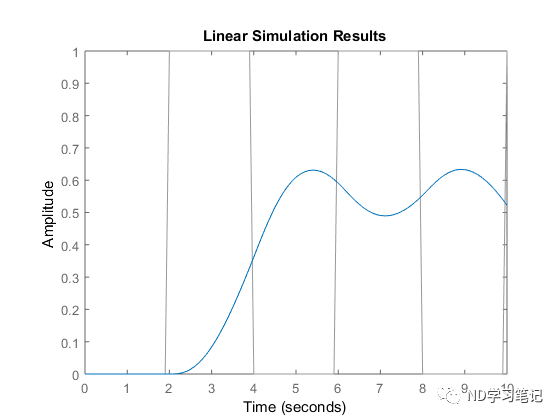
5.单位正弦 响应 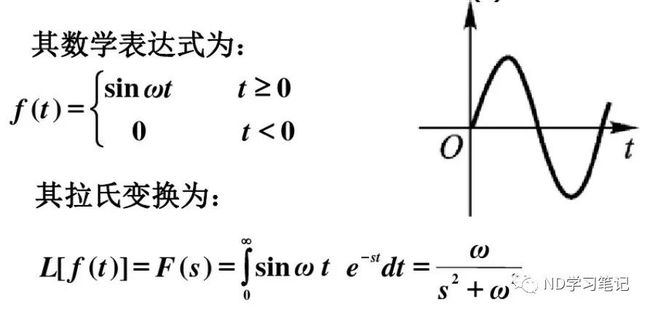 利用单位正弦相应可以获得系统对不同频率的稳态响应,进一步判断系统性能。 除了impulse和step函数MATLAB还提供很多时域分析函数。如initial零输入响应,convar白噪声方差 响应,lsim任意指定形式的输入响应。对于离散系统,只需要在对应函数名前加d,如dimpulse,dstep等。 例2:以方波信号作为输入,求例1中系统的响应曲线。 利用lsim函数编写如下的MATLAB代码:
利用单位正弦相应可以获得系统对不同频率的稳态响应,进一步判断系统性能。 除了impulse和step函数MATLAB还提供很多时域分析函数。如initial零输入响应,convar白噪声方差 响应,lsim任意指定形式的输入响应。对于离散系统,只需要在对应函数名前加d,如dimpulse,dstep等。 例2:以方波信号作为输入,求例1中系统的响应曲线。 利用lsim函数编写如下的MATLAB代码:



1.单位脉冲响应
时域分析法是基于时域响应的一种分析方法,所谓时域响应就是指系统在外部输入作用下的输出过程。根据外部输入不同,有单位脉冲响应,单位阶跃响应,单位斜坡响应、单位加速度响应,单位正弦响应等。
例1:求系统的单位脉冲响应
输入程序:A=[0 1 0;0 0 1;-1 -2 -3];B=[0;0;1];C=[1 0 0];sys=ss(A,B,C,D);impulse(sys) 可如前例使用step函数仿真 3.单位斜坡响应
可如前例使用step函数仿真 3.单位斜坡响应  4.单位加速度坡 响应
4.单位加速度坡 响应  5.单位正弦 响应
5.单位正弦 响应  利用单位正弦相应可以获得系统对不同频率的稳态响应,进一步判断系统性能。 除了impulse和step函数MATLAB还提供很多时域分析函数。如initial零输入响应,convar白噪声方差 响应,lsim任意指定形式的输入响应。对于离散系统,只需要在对应函数名前加d,如dimpulse,dstep等。 例2:以方波信号作为输入,求例1中系统的响应曲线。 利用lsim函数编写如下的MATLAB代码:
利用单位正弦相应可以获得系统对不同频率的稳态响应,进一步判断系统性能。 除了impulse和step函数MATLAB还提供很多时域分析函数。如initial零输入响应,convar白噪声方差 响应,lsim任意指定形式的输入响应。对于离散系统,只需要在对应函数名前加d,如dimpulse,dstep等。 例2:以方波信号作为输入,求例1中系统的响应曲线。 利用lsim函数编写如下的MATLAB代码:
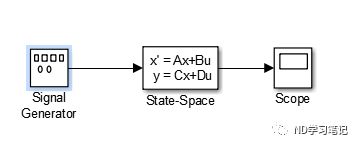
A=[0 1 0;0 0 1;-1 -2 -3];B=[0;0;1];C=[1 0 0];sys=ss(A,B,C,D);[u,t]=gensig('square',4,10,0.1);%获得方波信号lsim(sys,u,t)稳定性分析
控制系统能稳定工作是系统能够正常工作的首要条件。若系统在受到一定扰动的情况下仍能恢复平衡则称系统是稳定的。 系统稳定的必要和充分条件是其特征方程的根全部在s复平面的左半平面。如果有根在右半平面,系统不稳定,如果有根在虚轴上,系统处于临界稳定状态(振荡),如果有根在原点上,系统偏离平衡点,也不稳定。 MATLAB提供了直接求取零极点的zpk函数,可以根据零极点分布对系统稳定性进行判断。MATLAB还提供了直接求根函数roots,因此可以对特征方程求根来判断稳定性。 例3:已知单位负反馈开环传递函数为: 试判断该系统稳定性。 该系统闭环传递函数为: 根据劳斯判断易知该系统是不稳定的。 编写如下代码判断稳定性。z=1;p=[0 -0.1 -0.2];k=1;G0=zpk(z,p,k);G=feedback(G0,1); %单位负反馈sys1=tf(G)sys1 = s - 1 -------------------------- s^3 + 0.3 s^2 + 1.02 s - 1 Continuous-time transfer function.%下面利用zpk函数和roots函数确定稳定性sys2=zpk(sys1);sys2.p{:} %获得系统所有极点ans = -0.4627 + 1.1767i -0.4627 - 1.1767i 0.6255 + 0.0000iroots(sys1.den{:})ans = -0.4627 + 1.1767i -0.4627 - 1.1767i 0.6255 + 0.0000i
根轨迹绘制
MATLAB提供了pzmap函数用于绘制系统零极点,还提供了rlocus函数获得系统的根轨迹图。rlocus函数可以计算出根轨迹的n条分支,并以其选定的实轴和虚轴绘制图形。
注意:绘制根轨迹时,应令S平面实轴和虚轴的比例尺相同,这样才能反映S平面上坐标位置和相角的关系。在MATLAB中,可以利用axis equal命令来实现。
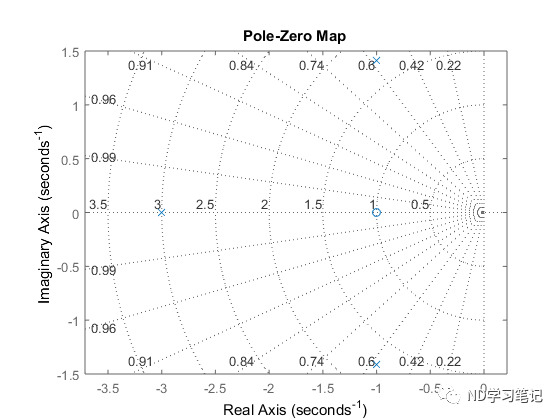
例4:已知系统闭环函数
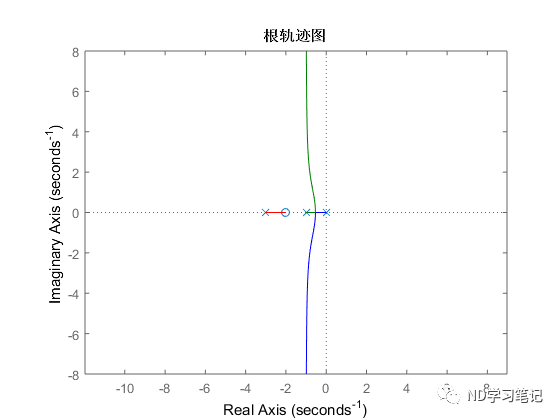
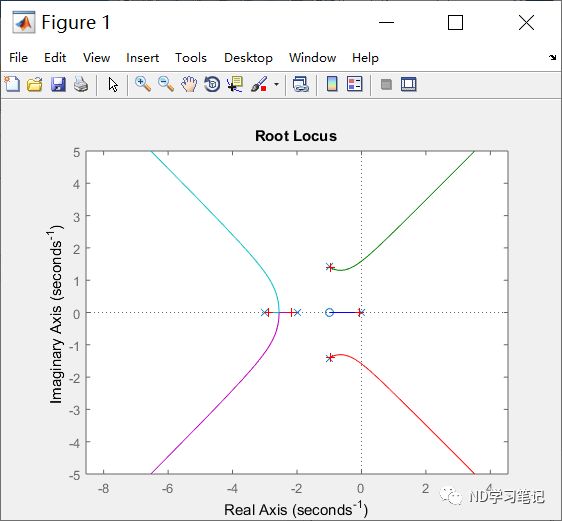
试绘制系统的零极点图。 编写如下MATLAB程序:clear allnum=2*[1 1];den=conv([1 2 3],[1,3]);sys=tf(num,den);sys1=zpk(sys);pzmap(sys1);axis equalgrid onclear allnum=[1 2];den=conv([1 0],conv([1 1],[1 3]));sys=tf(num,den);rlocus(sys)title('根轨迹图')axis equalMATLAB还提供了rlocfind函数,可以计算与根轨迹上指定极点相对应的根轨迹增益,适用于连续系统和离散系统。
基本语法为[k,poles]=rlocfind(sys),执行后根轨迹图窗口中会显示一个十字形光标,通过移动鼠标来选中指定极点,由k返回根轨迹增益,poles返回所有对应极点。
例6:已知单位负反馈系统开环传递函数为
试绘制根轨迹图,并选择一点,计算该点对应的增益K和其他闭环极点位置。
clear allnum=[1 1];den=conv([1 0],conv([1 2 3],[1 5 6]));sys=tf(num,den);rlocus(sys)axis equal[k,poles]=rlocfind(sys)