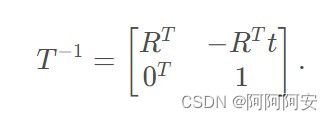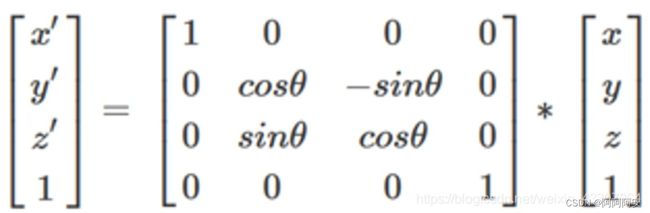点云配准（二） 三维刚体变换
一.欧式变换基础
刚体是指在理想状态下形状和大小都保持不变的物体。欧氏变换则是指保持了向量的长度和夹角都不发生改变的变换过程。刚体的欧式变换就相当于我们把一个刚体原封不动地进行了运动，而不改变它自身的形态，该变换过程可以由旋转和平移组合描述。
1.旋转变换推导
在某个三维向量空间坐标系中，空间的单位正交基为
（任意的线性无关向量组都可以通过施密特正交规范化转化为一组等价的单位正交向量组）。假设该向量空间/坐标系经过一次旋转后基底变为了 
。这时如果有同一个向量a，该向量在坐标系旋转前后都没有发生改变（长度相等且方向相同的两个向量是相等向量），改变的只是向量a在不同坐标系基底下的表示，所以向量a前后仍是等价的：
设向量a在两个坐标系下的坐标分别为![[a_1,a_2,a_3]^T](http://img.e-com-net.com/image/info8/8b679e265fe44eb2bbcfd0b6c3147bd1.gif){kind=small}
，![[a_1^{'},a_2^{'},a_3^{'}]^T](http://img.e-com-net.com/image/info8/0aa6701b9dc344788d670cc9e46fc89c.gif){kind=small}
，因为向量本身没变，所以根据坐标定义可以得到等式：
这个等式就可以将旋转前后的两个坐标系联系起来，描述了一种坐标系之间的旋转变换关系。由于 ![[e_1,e_2,e_3]](http://img.e-com-net.com/image/info8/586188cf7449489a8c47269449d76e6b.gif){kind=small}
是正交矩阵（单位正交向量基/组），所以![[e_1,e_2,e_3]^T = [e_1,e_2,e_3]^{-1}](http://img.e-com-net.com/image/info8/4da434b52426460d808da68925c25003.gif){kind=small}
，等式两边同左乘 ![[e_1,e_2,e_3]^T](http://img.e-com-net.com/image/info8/34a41420d161433b9761a2acc7d64d48.gif){kind=small}
得：
进一步我们可以将这个等式变换写作 
，其中矩阵R恰好由两组基的内积组成，刻画了旋转前后同一个向量的坐标变换关系，因此矩阵R被称为旋转矩阵；由于这两组基都是单位正交向量组，因此他们的内积恰好是两组基之间向量夹角的余弦值，故矩阵R也叫方向余弦矩阵。该矩阵的特点包括：
- 旋转矩阵R是正交矩阵：因为
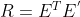，而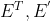 
均为正交矩阵，两个正交矩阵的乘积仍为正交矩阵，所以旋转矩阵R为正交矩阵。 
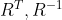描述了相反的变换：因为旋转矩阵R为正交矩阵，则
- 旋转矩阵R的行列式为1：三阶行列式的几何意义是行向量或列向量所围成几何立方体的体积。而旋转矩阵R为正交矩阵，列向量相互正交且模长为1，组成了一个长宽高均为1的立方体，因此体积为1即行列式必定为1。即旋转操作不会改变矩阵的面积/体积/向量关系，如果一个线性变换(矩阵)的行列式大于1，那么就会放大面积/体积；反之就会缩小面积/体积。
- 正交变换：正交变换是线性变换的一种，不会影响转换前后向量间的夹角和内积长度。其矩阵表示为正交矩阵，若|A|=1则表示旋转，否则|A|=-1表示反射。
2.平移变换推导
在欧式变换中，除了旋转变换还有平移变换。根据平移的定义，我们可以得到：
因此，上式可以表示为
，其中 t 为平移向量。至此，我们可以将旋转变换和平移变换组合起来，用一个旋转矩阵R和一个平移向量t完整的描述一个欧式空间的坐标变换即
。它表示先对a坐标系下做旋转变换，后做平移变换。
注意：先旋转后平移和先平移后旋转不是等价的，因为矩阵运算顺序是不能改变的（不满足交换律），但所有的欧式变换都可以统一转化为先旋转后平移的形式。
二.齐次坐标变换
1.齐次坐标的概念
在欧式变换中，用R、t来表示欧式空间的旋转和平移存在一个问题就是变换关系不是一个简单的线性关系，因此随着越来越复杂的变换，欧式变换的表现形式可能非常繁杂，比如
。因此人们希望能够进一步简化或统一一种简单的变换表示形式，就引入了齐次坐标。
齐次坐标就是在原n维坐标表示上增加了一个维度，使用n+1维来表示n维，在三维空间中其具体表示如下：
- 点的表示：增加一个维度，其数字为1。即
表示点a的齐次坐标 - 向量的表示：增加一个维度，其数字为0。即
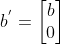表示向量b的齐次坐标 - 齐次坐标的运算规则：
- 齐次规范化：
](http://img.e-com-net.com/image/info8/16ff94541d234fdb9eb49d3e1631b97e.gif)
仍表示一个点，任何非齐次坐标都可以规范化到齐次坐标下，即![[x/w,y/w,z/w,1]](http://img.e-com-net.com/image/info8/847f4d00643d4cd6984270c95a540bb1.gif)
- vector + vector = vector、vector - vector = vector、point - point = vector
- point + vector = point：表示该点沿着向量平移后的点
- point + point = point：表示两点的中点
- 齐次规范化：
2.齐次坐标下的欧式变换
有了齐次坐标的表示之后，我们可以将之前的欧式变换表示转换到齐次坐标下，具体过程如下：
其中，左上角R为3x3的旋转矩阵，右上角t为3x1的平移向量，0和1都为齐次补充。可以看到，在齐次坐标下，旋转和平移都可以统一为一个齐次变换矩阵T，将非线性的欧式变换转换为了线性表示。同样，求解该矩阵的逆
，其结果表示一个反向的逆变换：
优点：有了齐次变换矩阵T之后，任何复杂的变换都可以通过不断累计左乘变换矩阵T来实现。并且，矩阵虽然不满足交换律但是满足结合律，任何复杂的变换 
都可以用一个3x3的矩阵来表示。
三.旋转变换的多种表示
1.旋转向量表示旋转
在上述欧拉变换中，使用旋转矩阵R表示旋转变换过程/关系存在一些问题如下：
- 不直观：通过旋转矩阵不能直观地看出旋转的方向和角度，假设给定一个旋转矩阵，要求旋转方向不变，旋转角度变成一半，那么新的旋转矩阵计算起来就比较麻烦了。
- 有冗余：旋转变换本身只有3个自由度，但旋转矩阵有9个元素，因此旋转矩阵中的元素不是相互独立的，这在非线性优化中会带来问题。
为了解决上述问题，我们希望能够有一种更加直观、紧凑的旋转表示方式，于是便有了旋转向量的表示。
（1）旋转向量定义
向量旋转公式最早由 Rodrigues 提出。任意旋转都可以描述为刚体绕某个旋转轴旋转了多少角度，用一个旋转轴和一个旋转角来刻画旋转变换。于是，我们可以用一个三维向量
来表示该旋转变换，该向量的方向是旋转轴，其模长是旋转角度。进一步，我们可以用该向量的单位向量
表示旋转轴方向，用旋转角
表示其模长，则 
。
根据罗德里格斯变换公式，我们可以得到三维点/向量 
在旋转向量 的作用下变换到 
的关系式为（推导过程可参考罗德里格斯与旋转向量）：
（2）旋转向量转换为旋转矩阵
我们进一步探究旋转向量与旋转矩阵之间的关系。由旋转变换公式可知：
，因此我们需要将上述旋转向量变换公式进行转化：
其中，
，
为单位矩阵。 因此，旋转矩阵R为：
（3）旋转矩阵转换为旋转向量
2.欧拉角表示旋转
由上述欧拉变换的推导可以看出，旋转矩阵的表示非常抽象，而欧拉角则提供了一种非常直观的方式来描述旋转过程。欧拉角是用来确定定点转动刚体位置的3个一组独立角参量，通俗点说，欧拉角就是一种将复杂三维旋转变换分解为分别绕三个独立轴转动角度的复合变换的描述，它使用了3个分离的转角，把一个旋转分解成3次绕不同轴的旋转。
2.1 不同的旋转定义
（1）旋转顺序/顺规
对于x，y，z三个轴的不同旋转顺序一共有(x-y-z, y-z-x, z-x-y, x-z-y, z-y-x, y-x-z)等六种组合，不同的旋转顺规会带来不同的结果。我们需要明确旋转顺序，才能确定最终欧拉角所指的姿态。
（2）旋转方式
由于旋转角的分解方式有很多种，欧拉角也存在不同的旋转定义方法，大致可分为两类，分别是：
- 外旋/静态欧拉角（常用）：外旋是指在物体旋转过程中绕固定的坐标轴旋转，旋转中的X,Y,Z轴都是固定不变的，一般为世界坐标系。举例为假设开始两个坐标系（世界固定坐标系A和物体本身坐标系B）初始重合，先将B绕A的X轴旋转α，然后绕A 的Y轴旋转β，最后绕A 的Z轴旋转γ，就能旋转到当前姿态。
- 内旋/动态欧拉角：内旋是指在物体旋转过程中绕自身坐标轴旋转，旋转中的X,Y,Z轴都是会随着自身的旋转而改变的。举例为假设开始两个坐标系（世界固定坐标系A和物体本身坐标系B）初始重合，先将B绕自身的Z轴旋转γ，然后绕变换后自身的Y轴旋转β ，最后绕再次变换后自身的X轴旋转α ，就能旋转到当前姿态。
注意两种旋转方式的旋转矩阵构造方式也是不同的，外旋为分解旋转矩阵依次从右向左累乘，内旋为分解旋转矩阵依次从左向右累乘。比如对于
的变换来说：
- 外旋
，P' = Rp - 内旋
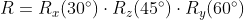，P' = Rp
（3）内旋与外旋的等效性
内在旋转与外在旋转的绕轴旋转序列相互倒序时，两者等效。即由于展开式相等，所以绕定轴X(a)-Y(b)-Z(c)旋转（外旋） 等价于 绕动轴Z(c)-Y(b)-X(a)旋转（内旋），二者作用下物体的最终旋转姿态是一样的。外旋与内旋只是欧拉角变换的不同定义表达方式，其表示的结果和作用是等价的。
对于该等效性的证明，理论上非常复杂且繁琐，这里不予说明。俗话说，实践出真知，我们来直接模拟一下两种旋转方式的最终旋转矩阵是否相同即可。模拟所使用的软件为Matlab，思路为（初始时两坐标系重合）：
- 先正常模拟外旋变换 X(30) -> Z(45) -> Y(60)，旋转矩阵 R = RyRzRx
- 再模拟内旋变换 Y(60)->Z'(45)->X''(30)，为了证明内外旋一致，这里使用旋转向量来求取内旋的旋转矩阵。假设初始时x=[1;0;0]，y=[0;1;0]；z=[0;0;1]，R = Rx''(30)Rz'(45)Ry(60)。其测试代码和结果如下：
%旋转向量变换：罗德里格斯公式求取旋转矩阵
% - u: 旋转轴向量
% - theta： 旋转角度
% - R： 旋转矩阵
function [ R ] = Rodrigues( u, theta )
ux = u(1);
uy = u(2);
uz = u(3);
R = [cos(theta) + ux^2*(1-cos(theta)),ux*uy*(1-cos(theta))-uz*sin(theta),uy*sin(theta) + ux*uz*(1-cos(theta));
uz*sin(theta)+ux*uy*(1-cos(theta)),cos(theta)+uy^2*(1-cos(theta)),-ux*sin(theta)+uy*uz*(1-cos(theta));
-uy*sin(theta)+ux*uz*(1-cos(theta)),ux*sin(theta)+uy*uz*(1-cos(theta)),cos(theta)+uz^2*(1-cos(theta))];
end%1.外旋 X(30) -> Z(45) -> Y(60)
Z = 45*pi/180; %rotation about z
Y = 60*pi/180; %rotation about y
X = 30*pi/180; %rotation about x
Rz1 = [cos(Z), -sin(Z), 0; sin(Z), cos(Z), 0; 0,0,1];
Ry1 = [cos(Y), 0, sin(Y); 0,1,0; -sin(Y), 0, cos(Y)];
Rx1 = [1,0,0; 0, cos(X), -sin(X); 0, sin(X), cos(X)];
R1 = Ry1*Rz1*Rx1;
R1
%2.内旋 Y(60)->Z'(45)->X''(30) 旋转向量
uy = [0;1;0];
ux = [1;0;0];
uz = [0;0;1];
Ry2 = Rodrigues(uy,Y);
uz2 = Ry2*uz;
ux2 = Ry2*ux;
Rz2 = Rodrigues(uz2,Z);
ux3 = Rz2*ux2;
Rx2 = Rodrigues(ux3,X);
R2 = Rx2*Rz2*Ry2;
R2
可以看出，内旋与外旋在旋转序列相反时，对物体的作用是等效的，物体将会被变换到同一姿态。
（4）欧拉角的万向锁问题
万向锁的定义：当仰俯角为 ± 90°时，欧拉角旋转的第一次旋转与第三次旋转使用同一个轴，会使得系统丢失一个自由度（由3次旋转变成了两次旋转），这被称为奇异性问题，或万向锁。
举个例子：假设我们按照z-y-x的顺序对物体进行旋转，先绕X轴旋转30度，再绕Y轴旋转90度，再绕Z轴旋转10度得到的最终姿态和先绕X轴旋转20度，再绕Y轴旋转90度的结果一样。因此相对于最初姿态而言，当一个欧拉角包含绕Y轴旋转90度时，绕X轴和绕Z轴旋转已经是在绕同一个轴在进行旋转，这个时候只有两个轴在起作用。这就是万向锁状态。
缺点：万向锁会使得欧拉角的表示方式并不唯一，即一种姿态会有多种欧拉角旋转方式。欧拉角的万向锁问题不能被完全规避，因此欧拉角不适用于插值和迭代，往往只用于人机交互中。
2.2 欧拉角到旋转矩阵
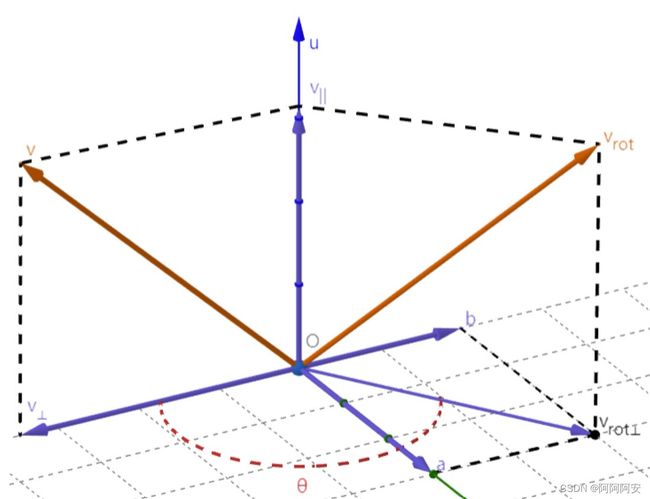
（1）绕x轴的旋转
在三维场景中，当一个点P(x,y,z)绕x轴旋转θ角得到点P’(x’,y’,z’)。由于是绕x轴进行的旋转，因此x坐标保持不变，相当于是在y和z组成的yoz（o是坐标原点）平面上进行的是一个二维的旋转，于是有（左/右手坐标系下一致，旋转方向按左/右手定则）：
（2）绕y轴的旋转
绕Y轴的旋转和绕X轴的旋转类似。旋转过程中Y坐标保持不变，相当于绕ZOX组成的平面进行了一次二维的旋转，同样有：
（3）绕z轴的旋转
与上面类似，绕Z轴旋转时Z坐标保持不变，相当于绕xoy组成的平面内进行了一次二维的旋转。我们也可以得到：
（4）组合旋转变换
组合旋转矩阵等于基本旋转矩阵的连乘，连乘顺序依基本旋转的先后次序由右向左排列（左乘坐标矩阵，默认外旋），因此顺规为ZYX的组合旋转矩阵为：
2.2 旋转矩阵到欧拉角
四.左手坐标系与右手坐标系
1.左右手坐标系的定义
（1）左手坐标系：伸开我们的左手, 掌心向外, 大拇指与食指成90度, 中指垂直指向屏幕,。大拇指指向的方向就是X轴正方向, 食指指向的方向就是Y轴正方向, 中指指向的方向就是Z轴正方向。左手坐标系中的旋转正方向满足左手定则，正方向为顺时针。使用左手坐标系的有 Unity、DirectX
（2）右手坐标系：伸开我们的右手, 掌心向内, 大拇指与食指成90度, 中指垂直指向自己,。大拇指指向的方向就是X轴正方向, 食指指向的方向就是Y轴正方向, 中指指向的方向就是Z轴正方向。右手坐标系中的旋转正方向满足右手定则，正方向为逆时针。使用右手坐标系的有 OpenGL、CMTracker
（3）区别与联系：
- 轴向相反：左手坐标系和右手坐标系中有一个轴的正方向是相反的，其他轴相同。比如，X轴和Y轴的方向是相同时, Z轴的方向相反；X轴和Z轴的方向相同时，Y轴的方向相反等。
- 旋向相反：左手坐标系和右手坐标系中的旋转正方向是相反的。
2.左右手坐标系下的变换关系
（1）行向量与列向量表示变换
- 列向量：在列向量表示下，刚体的三维旋转矩阵左乘，平移矩阵也为列向量；即
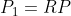
- 行向量：在行向量表示下，刚体的三维旋转矩阵右乘，平移矩阵也为行向量；旋转矩阵和平移矩阵均为列向量下的转置。即
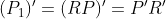
（2）坐标系下的变换表示相同
左手坐标系下+左手定则的欧式变换，和右手坐标系下+右手定则的欧式变换表达形式是一样的，都是P'=RP（列向量下），旋转平移变换矩阵也是一样的，都满足之前所计算的各种形式下的旋转矩阵和平移矩阵。
3.左右手坐标系之间的转换
同一个点P在左手坐标系和右手坐标系下有一个轴的坐标是相反的，我们以X轴为例。即
，假设空间中有变换矩阵S：
则左右手坐标系下点的变换即可用S来表示，即：
则左右手坐标系下变换之间的相互转换公式为（左手到右手和右手到左手是一样的，因为S为正交矩阵，
）：
注意：如果是其他轴（Y或Z）取反，则直接改变对应矩阵S即可，其他推导过程是一样的。详细证明与推导过程请见：https://www.jianshu.com/p/a58d941dec2d