三维空间刚体变换：欧拉角、旋转向量、四元数

除了使用旋转矩阵$R$来表示旋转外，还有其他许多常用的方式用于表示旋转：

欧拉角

欧拉角是一种相对直观的表示旋转效果的方法，它将一个旋转分解为绕三个轴进行旋转，由于分解顺序有多种，故而有不同的欧拉角。此处旋转较为经典的"偏航-俯仰-滚动"模型也即ZYX分解进行学习：

• 绕Z轴旋转，得到偏航角（Yaw）
• 绕旋转后的Y轴旋转，得到俯仰角（Pitch）
• 绕旋转后的X轴旋转，得到滚动角（Roll）

由此可用${\left[\begin{array}{ccc}r& p& y\end{array}\right]}^T$表达任意一个旋转，如图所示：

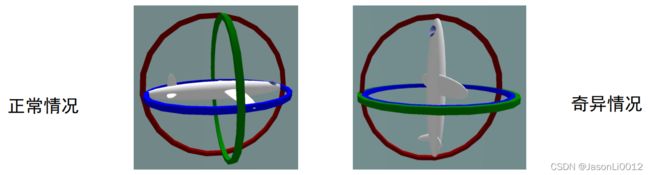
欧拉角存在的缺点在于，存在万向锁问题。当俯仰角为$\pm 90°$时，第一次旋转和第三次旋转使用的为同一个轴，也即系统丢失一个自由度（有三自由度变为二自由度）。

旋转向量（角轴）

旋转矩阵有九个元素，但仅存在三个自由度存在。而变换矩阵有十六个元素，但同样仅有六个自由度。同时由于旋转矩阵$R$和变换矩阵$T$为正交矩阵，难以优化。故而希望用一个三维向量来表示旋转，一个六维向量来表示变换。

任意一个旋转可通过一个等效转轴和一个等效转角 进行表示，定义一个向量，使其方向同等效转轴一致，其大小等于等效转角，称其为旋转向量（角轴，Axis-Angle）

定义转轴为单位长度的向量$n$，其转角为$\theta$，则采用罗德里格斯公式可得到由旋转向量到旋转矩阵的变换：
$$R=\cos \theta I+(1-\cos \theta )n{n}^T+\sin \theta n^{\wedge }$$
通常，用符号$vers\theta =1-\cos \theta$表示正矢函数：
$$R=\cos \theta I+vers\theta n{n}^T+\sin \theta n^{\wedge }$$
符号${}^{\wedge }$表示求反对称矩阵。

同样也可以得到由旋转矩阵到旋转向量的转换，对上式两侧求迹（trace）：
$$\begin{array}{rl}tr(R)=& \cos \theta tr(I)+vers\theta tr(n{n}^T)+\sin \theta tr(n^{\wedge })\\ =& 3\cos \theta +vers\theta +0\\ =& 3\cos \theta +1-\cos \theta \\ =& 1+2\cos \theta \end{array}$$
式中，$n$为单位向量，则$tr(n{n}^T)=1$；反对称矩阵主对角线元素为0，则$tr(n^{\wedge })=0$，由此得到旋转角表达式：
$$\theta =\arccos \frac{tr(R)-1}{2}$$
此外，旋转轴旋转后不发生变换，也即：
$$Rn=n$$
由此，转轴$n$是由矩阵$R$特征值为1的特征向量，求解方程并归一化可得。

四元数

四元数表示标准

四元数用复数形式表示旋转，具有一个实部和三个虚部，四元数是紧凑的，无奇异性的：
$$q=w+xi+yj+zk$$
其中，$i、j、k$为三个虚部，四元数有两种表示方法，分别对应不同标准。

Hamilton表示法（右手系）满足如下条件：
$$\{\begin{array}{l}{i}^2=j^2=k^2=-1\\ ij=k\\ ijk=-1\end{array}$$
JPL表示法（左手系）满足如下条件：
$$\{\begin{array}{l}{i}^2=j^2=k^2=-1\\ ij=-k\\ ijk=1\end{array}$$
Hamilton表示法被广泛运用在Eigen库、Ceres库、MATLAB、ROS等开源库、工具中，后续推导采用Hamilton表示法（右手系）。

可将$i、j、k$视为三个坐标轴，一般四元数也可以表示为一个标量和一个向量的形式：
$$q={\left[\begin{array}{cc}s& v\end{array}\right]}^T,s=w\in \Re ,v={\left[\begin{array}{ccc}x& y& z\end{array}\right]}^T\in {\Re }^3$$
称标量$s$为四元数的实部，矢量$v$为四元数的虚部。

当四元数的实部为零，称其为虚四元数；当四元数的虚部为零，称其为实四元数。

采用单位四元数可表示三维空间中的旋转。

四元数运算

定义两个四元数$q_1、q_2$：
$$\begin{gathered} q_1=w_1+x_{1}i+y_{1}j+z_{1}k={\left[\begin{array}{cc}{s}_1& v_1\end{array}\right]}^T \\ {q}_2=w_2+x_{2}i+y_{2}j+z_{2}k={\left[\begin{array}{cc}{s}_2& v_2\end{array}\right]}^T \end{gathered}$$

加减

四元数的加减法同复数一样：
$$q_1\pm q_2={\left[\begin{array}{cc}{s}_1\pm s_2& v_1\pm v_2\end{array}\right]}^T$$

乘法

两个四元数相乘可利用向量的内外积公式进行计算：
$$q_1{q}_2={\left[\begin{array}{cc}{s}_1{s}_2-v_1^T{v}_2& s_1{v}_2+s_2{v}_1+v_1\times v_2\end{array}\right]}^T$$
四元数的相乘顺序不可交换，这是因为使用到向量的外积。

模长

$$\Vert \begin{array}{c}q\end{array}\Vert =\sqrt{w^2+x^2+y^2+z^2}$$

易得，两四元数乘积的模长等于每个四元数模长的乘积：
$$\Vert \begin{array}{c}{q}_1{q}_2\end{array}\Vert =\Vert \begin{array}{c}{q}_1\end{array}\Vert \Vert \begin{array}{c}{q}_2\end{array}\Vert$$

共轭

四元数的共轭即为虚部求反：
$$q^{\ast }=w-xi-yj-zk={\left[\begin{array}{cc}s& -v\end{array}\right]}^T$$
同时，一个四元数同自身共轭的积等于其自身的向量内积，也即模长的平方：
$$q^{\ast }q=q{q}^{\ast }=q\cdot q={\Vert \begin{array}{c}q\end{array}\Vert }^2={\left[\begin{array}{cc}{s}^2+v^{T}v& 0\end{array}\right]}^T$$

逆

四元数的逆如下：
$$q^{-1}=\frac{q^{\ast }}{{\Vert \begin{array}{c}q\end{array}\Vert }^2}$$
易得，四元数和自身的逆的乘积为1：
$$q{q}^{-1}=q^{-1}q=1$$
同时，四元数乘积的逆具有矩阵的特性：

$$(q_1{q}_2{)}^{-1}=q_2^{-1}{q}_1^{-1}$$

数乘

四元数也可以和常数相乘：
$$aq=aw+axi+ayj+azk={\left[\begin{array}{cc}as& av\end{array}\right]}^T$$

四元数表示旋转

对于三维空间内的一个点$p={\left[\begin{array}{ccc}x& y& z\end{array}\right]}^T\in {\Re }^3$，可以使用一个单位四元数 $q$指定其旋转。此处假设该点旋转至$p^{{}^{\prime }}$点，则首先用四元数形式来描述该点坐标：
$$p={\left[\begin{array}{cccc}0& x& y& z\end{array}\right]}^T={\left[\begin{array}{cc}0& v\end{array}\right]}^T$$
也即将坐标系三个轴同单位四元数的三个虚部所在空间相对应。对于旋转后的点$p^{{}^{\prime }}$可用如下方式进行计算：
$$p^{{}^{\prime }}=qp{q}^{-1}$$
所得结果为纯虚四元数，三个虚部对应三个轴坐标。

四元数与其他表示的转变

运算算子

对于一个四元数$q={\left[\begin{array}{cc}s& v\end{array}\right]}^T={\left[\begin{array}{cccc}w& x& y& z\end{array}\right]}^T$，定义算子$q^{+}$和$q^{\oplus }$：
$$q^{+}=\left[\begin{array}{cc}s& -v^T\\ v& sI+v^{\wedge }\end{array}\right]q^{\oplus }=\left[\begin{array}{cc}s& -v^T\\ v& sI-v^{\wedge }\end{array}\right]$$
上述算子将四元数映射至$4\times 4$的矩阵，由此可将四元数的乘法写为矩阵形式：
$$q_1^{+}{q}_2=\left[\begin{array}{cc}{s}_1& -v_1^T\\ v_1& s_{1}I+v_1^{\wedge }\end{array}\right]\left[\begin{array}{c}{s}_2\\ v_2\end{array}\right]=\left[\begin{array}{c}{s}_1{s}_2-v_1^T{v}_2\\ s_1{v}_2+s_2{v}_1+v_1^{\wedge }{v}_2\end{array}\right]=q_1{q}_2$$
也即，易得如下等式成立：
$$q_1{q}_2=q_1^{+}{q}_2=q_2^{\oplus }{q}_1$$

四元数到旋转矩阵

使用旋转矩阵表示某点旋转至另一点如下所示：
$$p^{{}^{\prime }}=Rp$$
首先，将四元数表示旋转的形式化为算子形式：
$$\begin{array}{rl}{p}^{{}^{\prime }}=& qp{q}^{-1}\\ =& q^{+}{p}^{+}{q}^{-1}\\ =& q^{+}(q^{-1}{)}^{\oplus }p\end{array}$$
将式中$q^{+}{q}^{-1^{\oplus }}$展开：
$$\begin{array}{rl}{q}^{+}(q^{-1}{)}^{\oplus }=& \left[\begin{array}{cc}s& -v^T\\ v& sI+v^{\wedge }\end{array}\right]\left[\begin{array}{cc}s& v^T\\ -v& sI+v^{\wedge }\end{array}\right]\\ =& \left[\begin{array}{cc}1& 0\\ 0^T& v{v}^T+s^{2}I+2s{v}^{\wedge }+(v^{\wedge }{)}^2\end{array}\right]\end{array}$$
已知$p$与点$p^{{}^{\prime }}$为纯虚四元数，也即$s_p=s_{p^{{}^{\prime }}}0$，则上式矩阵中右下角元素同旋转矩阵等价：
$$R=v{v}^T+s^{2}I+2s{v}^{\wedge }+(v^{\wedge }{)}^2$$

也即：
$$R=\left[\begin{array}{ccc}{x}^2-y^2-z^2+w^2& 2xy-2wz& 2xz+2wy\\ 2xy+2wz& y^2-x^2-z^2+w^2& 2yz-2wx\\ 2xz-2wy& 2yz+2wx& z^2-x^2-y^2+w^2\end{array}\right]$$
由于单位四元数模长为1：$x^2+y^2+z^2+w^2=1$，故而对主对角线进行化简：
$$R=\left[\begin{array}{ccc}1-2y^2-2z^2& 2xy-2wz& 2xz+2wy\\ 2xy+2wz& 1-2x^2-2z^2& 2yz-2wx\\ 2xz-2wy& 2yz+2wx& 1-2x^2-2y^2\end{array}\right]$$
上式所得旋转矩阵为Hamilton表示法下的旋转矩阵，若使用JPL表示法，则得到的旋转矩阵应为上式的转置矩阵：
$$R_{JPL}=(R_{Ham}{)}^T$$

旋转矩阵到四元数：

设旋转矩阵如下：
$$R=\left[\begin{array}{ccc}{r}_{11}& r_{12}& r_{13}\\ r_{21}& r_{22}& r_{23}\\ r_{31}& r_{32}& r_{33}\end{array}\right]$$
首先，对矩阵对角线元素进行加减运算：
$$\begin{array}{rl}{r}_{11}+r_{22}+r_{33}=& 4w^2-1\\ r_{12}+r_{21}=& 4xy\\ r_{12}-r_{21}=& 4wz\\ r_{31}+r_{13}=& 4xz\\ r_{31}-r_{13}=& 4wy\\ r_{23}+r_{32}=& 4yz\\ r_{23}-r_{32}=& 4wx\end{array}$$
解的$w$的值如下：
$$w=\frac{\sqrt{r_{11}+r_{22}+r_{33}+1}}{2}$$
同样，可以使用对角线得到$x、y、z$的值：
$$\begin{gathered} x=\frac{\sqrt{r_{11}-r_{22}-r_{33}+1}}{2} \\ y=\frac{\sqrt{-r_{11}+r_{22}-r_{33}+1}}{2} \\ z=\frac{\sqrt{-r_{11}-r_{22}+r_{33}+1}}{2} \end{gathered}$$
此处应注意，由于开方无法确定每一个数值的正负号。故而计算时应使用上述四个公式中的某一个计算得到四元数四个值中的一个后，带入如下公式计算其余量：
$$\begin{gathered} w=\frac{\sqrt{r_{11}+r_{22}+r_{33}+1}}{2}\Rightarrow x=\frac{r_{23}-r_{32}}{4w}y=\frac{r_{31}-r_{13}}{4w}z=\frac{r_{12}-r_{21}}{4w} \\ x=\frac{\sqrt{r_{11}-r_{22}-r_{33}+1}}{2}\Rightarrow w=\frac{r_{23}-r_{32}}{4x}y=\frac{r_{12}+r_{21}}{4x}z=\frac{r_{31}+r_{13}}{4x} \\ y=\frac{\sqrt{-r_{11}+r_{22}-r_{33}+1}}{2}\Rightarrow w=\frac{r_{31}-r_{13}}{4y}x=\frac{r_{12}+r_{21}}{4y}z=\frac{r_{23}+r_{32}}{4y} \\ z=\frac{\sqrt{-r_{11}-r_{22}+r_{33}+1}}{2}\Rightarrow w=\frac{r_{12}-r_{21}}{4z}x=\frac{r_{31}+r_{13}}{4z}z=\frac{r_{23}+r_{32}}{4z} \end{gathered}$$

此时，由于四元数$q$与$-q$表示同一个位姿，故而不考虑正负号问题。

四元数到旋转向量

对$R=v{v}^T+s^{2}I+2s{v}^{\wedge }+(v^{\wedge }{)}^2$求迹：
$$\begin{array}{rl}tr(R)=& tr(v{v}^T+s^{2}I+2s{v}^{\wedge }+(v^{\wedge }{)}^2)\\ =& tr(v{v}^T)+s^{2}tr(I)+2str(v^{\wedge })+tr((v^{\wedge }{)}^2)\\ =& (x^2+y^2+z^2)+s^2\cdot 3+2s\cdot 0-2(x^2+y^2+z^2)\end{array}$$
式中，已知单位四元数$q$的模长为一：
$${\Vert \begin{array}{c}q\end{array}\Vert }^2=w^2+x^2+y^2+z^2=1$$
其中，$w$为四元数的实部，也即$s=w$，则带入上式可得：
$$\begin{array}{rl}tr(R)=& (1-s^2)+3s^2+0-2(1-s^2)\\ =& 4s^2-1\end{array}$$
由角轴旋转角计算公式知：
$$\begin{array}{rl}\theta =& \arccos \frac{tr(R)-1}{2}\\ =& \arccos (2s^2-1)\end{array}$$
由三角公式可得：
$$\begin{gathered} \cos \theta =2{\cos }^2\frac{\theta }{2}-1 \\ 2s^2-1=2{\cos }^2\frac{\theta }{2}-1 \end{gathered}$$
由此得到：
$$\theta =2\arccos s$$
旋转轴可由四元数的虚部除以模长得到：
$${\left[\begin{array}{ccc}{n}_x& n_y& n_z\end{array}\right]}^T={\left[\begin{array}{ccc}x& y& z\end{array}\right]}^T/\sin \frac{\theta }{2}$$

旋转向量到四元数

同样，可得旋转向量到四元数的表达式：
$$q={\left[\begin{array}{cccc}\cos \frac{\theta }{2}& n_x\sin \frac{\theta }{2}& n_y\sin \frac{\theta }{2}& n_z\sin \frac{\theta }{2}\end{array}\right]}^T$$