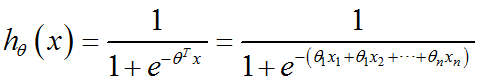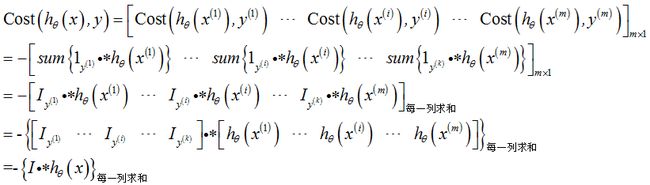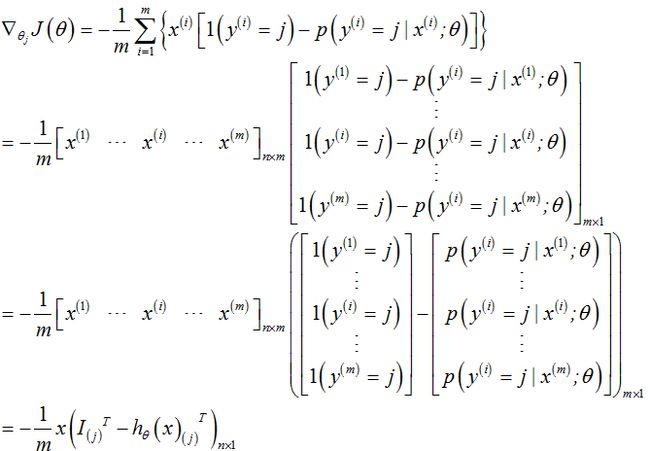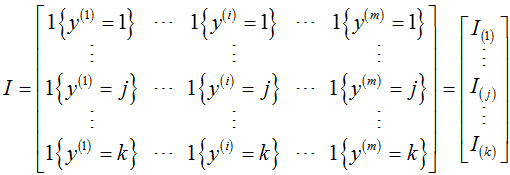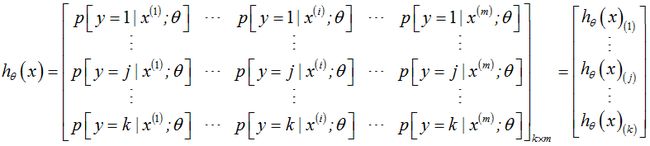UFLDL教程（四）之Softmax回归

 

关于Andrew Ng的machine learning课程中，有一章专门讲解逻辑回归（Logistic回归），具体课程笔记见另一篇文章。

下面，对Logistic回归做一个简单的小结：

给定一个待分类样本x，利用Logistic回归模型判断该输入样本的类别，需要做的就是如下两步：

① 计算逻辑回归假设函数的取值hθ(x)，其中n是样本的特征维度

② 如果hθ(x)>=0.5，则x输入正类，否则，x属于负类

或者直接利用判别边界进行判断，即：如果θ'x>=0，则x输入正类，否则，x属于负类                                                                            

所以，Logistic回归只能解决两类分类问题。

************************

这里一个很重要的问题就是，在对待分类样本进行分类之前，需要利用训练样本对该逻辑回归模型的参数θ=[θ1, θ2, ..., θn]进行求解

最优化的模型参数就是使代价函数取得最小值的参数，所以，只要利用优化，找到使得代价函数具有最小值的参数即可。

（1）给定参数theta的初始值

（2）利用函数fminunc对代价函数进行优化，求得最优化的theta值

      该函数要求输入theta的初始值、梯度和代价函数的计算函数、其他设置

（3）得到最优化的theta值后，对于某一个待分类样本，计算它的假设函数取值或者是判定边界的取值，从而可以对其分类进行判别

************************

 下面开始是softmax回归问题

  

第0步：初始化参数

①样本特征维数n (inputSize)

②样本类别数k (numClasses)

③衰减项权重  (lambda)

 

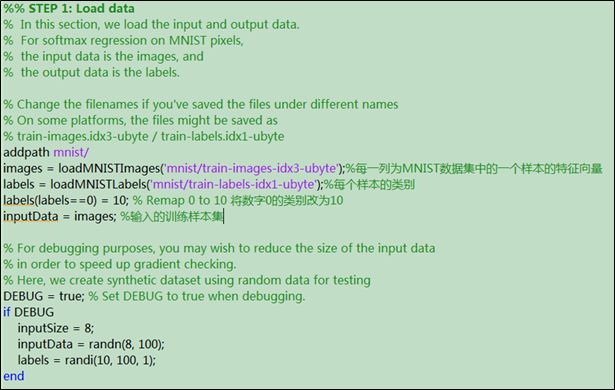
第一步：载人MNIST数据集

① 载入MNIST数据集

② 载入MNIST数据集的标签

在标签集中，标签0表示数字0，为了后续处理方便，将数字0的标签改为10

注1：实验中，有时为了调试方便，在调试时，可以加入合成数据；

注2：程序文件夹中，为了分类方便，将MNIST数据集和MNIST数据集的操作函数都存放在MNIST文件夹中，在使用前，加入语句addpath mnist/即可；

 

随机产生参数theta的初始值

它的维数是k*n，k是类别数numClasses，n是输入样本的特征维数inputSize

 

第二步：编写softmax函数

该函数的作用是计算代价函数及代价函数的梯度

（1）计算代价函数

① 代价函数的计算公式如下：

② 程序中的向量化计算方法如下:

(2) 计算梯度

① 梯度的计算公式如下：

② 程序中向量化计算方法如下：

 

第三步：梯度检验

在首次编写完softmax函数后，要利用梯度检验算法，验证编写的softmaxCost函数是否正确；直接调用checkNumericalCradient函数

 

第四步：利用训练样本集学习Softmax的回归参数

 

第五步：对于某一个待分类样本，利用求得的softmax回归模型对其进行分类

 

 

******关于向量化的程序公式的推导******

（1）已知参数的形式

① 参数θ的形式

② 输入数据x的形式

③ θx的乘积形式，记为矩阵M

（2）单个样本的成本函数

① 单个样本的成本函数

即：

② 单个样本的假设函数

但实际中，为了不会出现计算上的溢出，需要对假设函数的每一项都做如下调整

其中：

则有：

（3）m个样本的成本函数

① m个样本的成本函数

② m个样本的假设函数

其中：

(4) 计算梯度

① 单个样本的梯度计算

注1：

注2：

② m个样本梯度的计算

则有：

 

 

******按照神经网络的形式理解softmax模型******

（1）softmax模型，可以以神经网路的形式绘制，如下图所示

 

可以看到，softmax模型与传统的神经网络相比，只是输出层所使用的函数发生了变化：softmax模型使用的是指数函数，而神经网络使用的是sigmoid函数；

转载于:https://www.cnblogs.com/lutingting/p/4768882.html