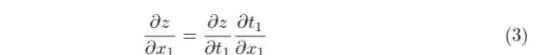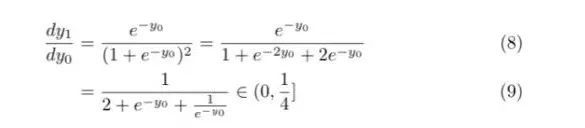【机器学习】详解 BackPropagation 反向传播算法!
首先介绍一下链式法则

假如我们要求z对x1的偏导数,那么势必得先求z对t1的偏导数,这就是链式法则,一环扣一环
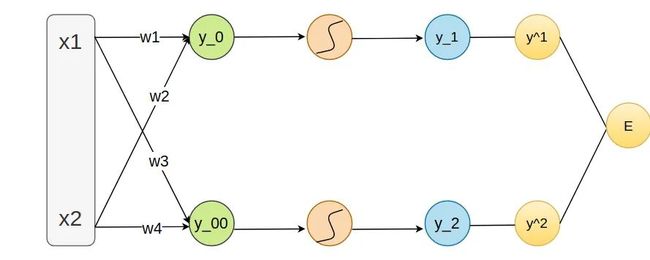
BackPropagation(BP)正是基于链式法则的,接下来用简单的前向传播网络为例来解释。里面有线的神经元代表的sigmoid函数,y_1代表的是经过模型预测出来的,y_1 = w1 * x1 + w2 * x2,而y^1代表的是实际值,最后是预测值与实际值之间的误差,l_1 = 1/2 * (y_1 - y^1)^2,l_2同理。总的错误是E = l_1 + l_2。
在神经网络中我们采用梯度下降(Gradient Descent)来进行参数更新,最终找到最优参数。可是离E最近的不是w1,首先我们需要求出E对l_1的偏导,接着求l_1对于最近神经元sigmoid中变量的导数,最后再求y_0对于w1的偏导,进行梯度更新。
这便是神经网络中的BP算法,与以往的正向传播不同,它应该是从反向的角度不断优化
这里只是用了一层隐含层,可以看的出来一个参数的梯度往往与几个量产生关系:
最终y被预测的值。这往往取决于你的激活函数,如这里采用sigmoid
中间对激活函数进行求导的值
输入的向量,即为x
推广到N层隐含层,只是乘的东西变多了,但是每个式子所真正代表的含义是一样的。
换个角度说,在深度学习梯度下降的时候会出现比较常见的两类问题,梯度消失以及梯度爆炸很可能就是这些量之间出了问题,对模型造成了影响。
1、梯度消失(Gradient Vanishing)。意思是梯度越来越小,一个很小的数再乘上几个较小的数,那么整体的结果就会变得非常的小。那么导致的可能原因有哪些呢?我们由靠近E的方向向后分析。
激活函数。y_1是最后经过激活函数的结果,如果激活函数不能很好地反映一开始输入时的情况,那么就很有可能出问题。sigmoid函数的性质是正数输出为大于0.5,负数输出为小于0.5,因为函数的值域为(0,1),所以也常常被用作二分类的激活函数,用以表示概率。但是,当x比较靠近原点的时候,x变化时,函数的输出也会发生明显的变化,可是,当x相当大的时候,sigmoid几乎已经是无动于衷了,x相当小的时候同理。这里不妨具体举个二分类的例子,比如说用0,1代表标签,叠了一层神经网络,sigmoid函数作为激活函数。E对l_1的偏导极大程度将取决于y_1,因为标签就是0,1嘛。就算输入端的x,w都比较大,那么经过sigmoid压缩之后就会变得很小,只有一层的时候其实还好,但是当层数变多之后呢,sigmoid函数假如说每一层都当做是激活函数,那么最后E对l_1的偏导将是十分地小,尽管x,w代表着一些信息,可经过sigmoid压缩之后信息发生了丢失,梯度无法完成真正意义上的传播,乘上一个很小的数,那么整个梯度会越来越小,梯度越小,说明几乎快收敛了。换句话说,几乎没多久就已经收敛了。
另一种思路是从公式(4)出发,无论y_0取何值,公式(4)的输出值总是介于(0,1/4](当然具体边界处是否能取到取决于具体变量的取值),证明:
因为不断乘上一个比较小的数字,所以层数一多,那么整个梯度的值就会变得十分小,而且这个是由sigmoid本身导致,应该是梯度消失的主因。
解决方法可以是换个激活函数,比如RELU就不错,或者RELU的变种。
2、梯度爆炸(Gradient Exploding)。意思是梯度越来越大,更新的时候完全起不到优化的作用。其实梯度爆炸发生的频率远小于梯度消失的频率。如果发生了,可以用梯度削减(Gradient Clipping)。
梯度削减。首先设置一个clip_gradient作为梯度阈值,然后按照往常一样求出各个梯度,不一样的是,我们没有立马进行更新,而是求出这些梯度的L2范数,注意这里的L2范数与岭回归中的L2惩罚项不一样,前者求平方和之后开根号而后者不需要开根号。如果L2范数大于设置好的clip_gradient,则求clip_gradient除以L2范数,然后把除好的结果乘上原来的梯度完成更新。当梯度很大的时候,作为分母的结果就会很小,那么乘上原来的梯度,整个值就会变小,从而可以有效地控制梯度的范围。
另外,观察公式可知,其实到底对谁求偏导是看最近的一次是谁作为自变量,就会对谁求,不一定都是对权重参数求,也有对y求的时候。
接着我们用PyTorch来实操一下反向传播算法,PyTorch可以实现自动微分,requires_grad 表示这个参数是可学习的,这样我们进行BP的时候,直接用就好。不过默认情况下是False,需要我们手动设置。
import torch
x = torch.ones(3,3,requires_grad = True)
t = x * x + 2
z = 2 * t + 1
y = z.mean()接下来我们想求y对x的微分,需要注意这种用法只能适用于y是标量而非向量
y.backward()
print(x.grad)所以当y是向量形式的时候我们可以自己来算,如
x = torch.ones(3,3,requires_grad = True)
t = x * x + 2
y = t - 9如果计算y.backward()会报错,因为是向量,所以我们需要手动算v,这里就是y对t嘛,全为1,注意v的维度就行。
v = torch.ones(3,3)
y.backward(v)
print(x.grad)往期精彩回顾
适合初学者入门人工智能的路线及资料下载机器学习及深度学习笔记等资料打印机器学习在线手册深度学习笔记专辑《统计学习方法》的代码复现专辑
AI基础下载机器学习的数学基础专辑黄海广老师《机器学习课程》视频课本站qq群851320808,加入微信群请扫码: