利用Q-learning解决Cliff-walking问题

利用Q-learning解决Cliff-walking问题

一、概述
1.1 Cliff-walking问题
悬崖寻路问题是指在一个4*10的网格中，智能体以网格的左下角位置为起点，右下角位置为终点，通过不断的移动到达右下角终点位置的问题。智能体每次可以在上、下、左、右这4个方向中移动一步，每移动一步便会得到-1单位的奖励。但是智能体在移动的过程中有以下的限制：

(1)智能体不能移出网格，如果智能体想执行某个动作移出网格，那么这一步智能体不会移动，但是这个操作依然会得到-1单位的奖励；
(2)如果智能体掉入悬崖，则会立即回到起点位置重新开始移动，并且会得到-100单位的奖励；
(3)当智能体移动到终点时，该回合结束，该回合总奖励为各步奖励之和。

1.2 Q-learning算法
Q-learning算法是强化学习算法中基于值函数的算法，Q即Q（s,a）就是在某一时刻s状态下(s∈S)，采取a(a∈A)动作能够获得收益的期望，环境会根据智能体的动作反馈相应的奖励。所以算法的主要思想就是将State与Action构建成一张Q-Table来存储Q值，以State为行、Action为列，通过每个动作带来的奖赏更新Q-Table，然后根据Q值来选取能够获得最大收益的动作。
Q-learning算法也是off-policy的算法。因为它在计算下一状态的预期收益时使用了max操作，直接选取最优动作，而当前policy并不一定能选到最优动作，因此这里生成样本的policy和学习时的policy不同，故也将其称作off-policy算法。

二、Q-learning解决Cliff-walking
2.1 Cliff环境创建
Cliff环境即悬崖环境，是指由人为创建的一个点阵网格，该网格的左下角位置为起点，右下角位置为终点，具体如图1所示。

图1：悬崖环境样例

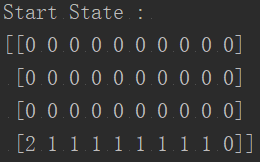
在实际创建过程中，悬崖环境的长和宽都是可以指定的，在本次复现代码中，我们选定整个悬崖环境的长为10，宽为4，即构造一个4*10的网格，以此来模拟4行10列的悬崖环境，创建的悬崖环境如图2所示。

图2：悬崖环境实现

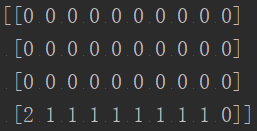
其中，数字2代表当前位置，数字1代表悬崖，数字0代表安全位置。
悬崖环境创建代码如下：

self.grid = np.zeros((self.height, self.length), dtype=np.int32)
self.grid[self.height - 1, 1: self.length - 1] = 1
self.agent_loc = [self.height - 1, 0]
self.goal_loc = [self.height - 1, self.length - 1]

2.2 Q-learning决策过程
Q-learning中，每个Q(s,a)对应一个相应的Q值，在学习过程中根据Q值选择动作，Q值是执行当前相关动作并且按照某一个策略执行下去所得到的回报总和，最优Q值可表示为Q^*，定义如下：

图3：Q-learning算法

Q-learning算法描述如上图所示。每次更新我们都用到了Q现实值和Q估计值, 而且Q-learning在Q(s1,a2)中也包含了一个Q(s2)的最大估计值。
其中，ε-greedy(贪婪算法)是用在决策上的一种策略，比如 ε=0.9时，就说明有90%的情况会按照Q表的最优值选择行为，10%的时间随机选行为。α是一个小于1的数，代表训练过程中的学习率，决定这次的误差有多少是要被学习的。γ是对未来reward的衰减值。
我们在复现过程中，分别按照5个步骤来实现Q-learning算法：
（1）初始化Q表格
Q表格（Q-Table）是在每个状态下我们计算最大期望奖励的查询表格，这个表格将指导我们在每个状态采取最佳行动。
我们首先建立一个有n列(n是动作的数量)，m行(状态数)的Q-table，初始化所有数值为0.0，代码实现如下：

np.ones(self.numActs).copy() * self.initValue

（2）动作选择
智能体在当前状态(s)下根据Q-table选择一个动作(a)，并在选择动作的过程中加入贪婪算法策略，实现如下：

if np.random.rand() <= self.epsilon:
return random.randrange(self.numActs)

在我们复现过程中只有四个动作，分别为：UP、DOWN、LEFT、RIGHT：

self.act_map["UP"] = 0
self.act_map["DOWN"] = 1
self.act_map["LEFT"] = 2
self.act_map["RIGHT"] = 3

（3）执行动作
当智能体完成动作选择后，便根据动作移动策略进行相应的移动。实现如下：

if action == 0:
	self.agent_loc[0] -= 1
	if self.agent_loc[0] < 0:
	   self.agent_loc[0] = 0
elif action == 1:
    self.agent_loc[0] += 1
    if self.agent_loc[0] > self.height - 1:
       self.agent_loc[0] = self.height - 1
elif action == 2:
	self.agent_loc[1] -= 1
    if self.agent_loc[1] < 0:
    	self.agent_loc[1] = 0
else:
	self.agent_loc[1] += 1
	if self.agent_loc[1] > self.length - 1:
		self.agent_loc[1] = self.length - 1
reward = -1
if self.grid[self.agent_loc[0], self.agent_loc[1]] == 1:
	reward = -100
	self.agent_loc = [self.height - 1, 0]
if self.agent_loc == self.goal_loc:
    done = True
else:
	done = False

（4）计算奖励
在智能体完成动作后，比如上、下、左或者是右，每正常完成一次动作操作时，便给于其-1单位的奖励。如果智能体掉入悬崖，则给于其-100单位的奖励，且需回到初始位置重新开始。如果智能体到达终点，则记录相关reward，并重新开始下一轮。

（5）更新Q表
当这一轮训练完成后，根据Q-learning算法计算相应的Q值，并将最新计算出的Q值更新到Q表中，实现如下：

bootstrappedTarget = reward + self.Factor * np.max(self.qDict[nextState])
currentEstimate = self.qDict[prevState][action]
tdError = bootstrappedTarget – currentEstimate
self.qDict[prevState][action] += self.learningRate * tdError

三、实验结果
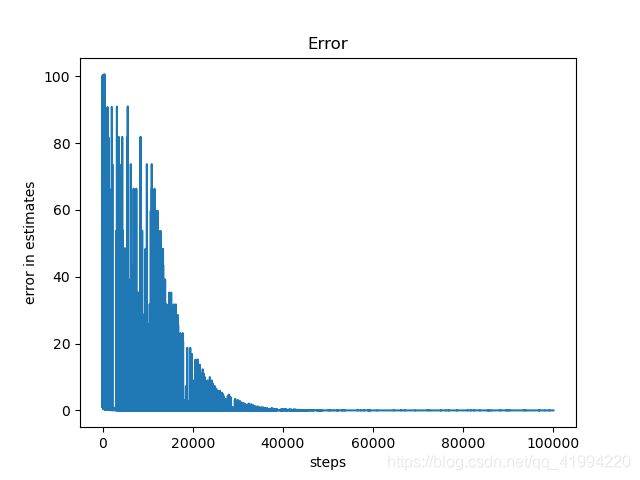
3.1 Q表误差
在对智能体不断迭代训练其到目标地点的最短路径时，我们会对当前计算的Q表值与前一次的Q表值进行求差值，并对求取的差值进行绝对值化，这一部分代码在实现上较为简单：

tdError = bootstrappedTarget – currentEstimate
self.tdErrorList.append(np.absolute(tdError))

我们可以将每次迭代的Q表值误差画出来，以便观察：

图4：Error曲线

上图是智能体的学习曲线，可以看出大约35000个steps之后，智能体开始找到了最优路径，到100000个steps过程中会有瑕疵，是因为ε-greedy的ε参数并没有完全衰减到足够小，以至于会有随机动作的产生，到了90000个steps之后，ε越来越靠近0，行为策略逐渐变成了目标策略。从另一个角度看，行为策略逐渐变成了确定性策略，那么就不会出现随机动作的情况，每一步的都是贪婪策略，其路径就是唯一的，即最优策略产生了。

3.2 奖惩值
智能体每正常完成一次动作操作时，便给于其-1单位的奖励，掉入悬崖时，则给于其-100单位的奖励，故我们需要对其每次迭代学习的奖励（reward）进行记录分析。我们可以将每次迭代的reward画出来，以便观察：

图5：reward曲线

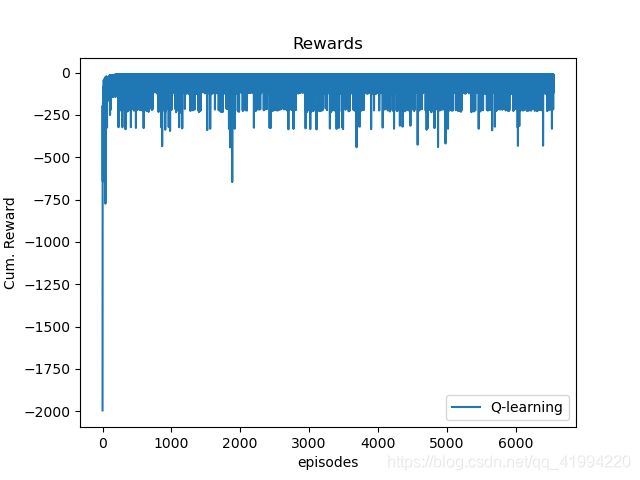
可以看出大约在150个steps之前，reward上升的非常快，reward和在快速变少，即奖励绝对值变小，这说明了智能体对路径的学习较快，很容易就能够找到最优路径。在这之后，reward就不断震荡，这与ε-greedy的ε参数有关。
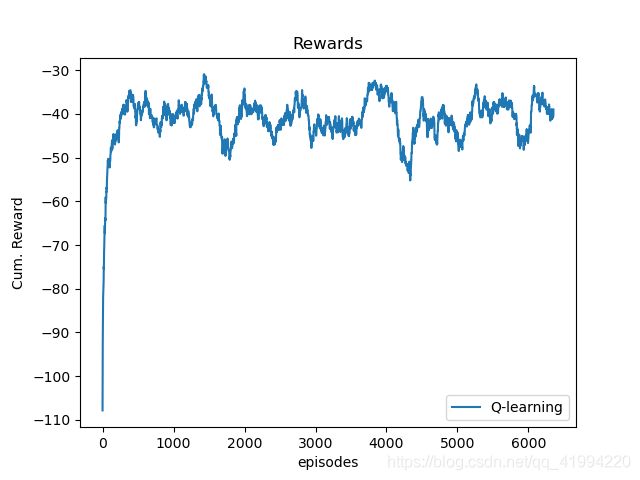
为了更好的展现reward的曲线趋势情况，我们运用滑动平均算法来对reward进行平滑处理，其实现代码如下：

def moving_average(a, n=3):
    ret = np.cumsum(a, dtype=float)
    ret[n:] = ret[n:] - ret[:-n]
    return ret[n - 1:] / n
Rewards = moving_average(QLS.cumRewards, n=200)

当对reward处理完毕后，我们再对其画曲线图：

图6：滑动平均后的reward曲线

此时，对于reward的上升降趋势就十分明显了。

3.3 规划路径展现
智能体在经过多次迭代训练后，最终找到了一条最优路径，即贴着悬崖边进行移动，这样的路径是最短的路径。

图7：智能体规划的路径

由上图所示，上边的图是智能体开始在网格中的位置，从图中可以看出，智能体开始位置在左下角。为了到达目的地，即右下角位置，智能体通过1次UP动作、9次RIGHT动作以及1次DOWN动作，最终实现到达目的地。具体路径如下边图中红线所示。

四、总结
Q-learning是一种基于值的监督式强化学习算法，它根据Q函数找到最优的动作。在悬崖寻路问题上，Q-learning更新Q值的策略为ε-greedy(贪婪策略)。其产生数据的策略和更新Q值的策略不同，故也成为off-policy算法。
对于Q-leaning而言，它的迭代速度和收敛速度快。由于它每次迭代选择的是贪婪策略，因此它更有可能选择最短路径。由于其大胆的特性，也侧面反映出它的探索能力较强。不过这样更容易掉入悬崖，故每次迭代的累积奖励也比较少。

附上python实现代码（代码是参考了多位大佬代码而改写成的，我也在关键处（基本上都有）加上了注释，便于各位阅读）：
GitHub：https://github.com/DeepVegChicken/Learning-QLearning_SolveCliffWalking

# *_* coding:utf-8 _*_
# 开发团队: 喵里的猫
# 开发人员: XFT
# 开发时间: 2021/6/21 16:13
# 文件名称: QLearning_SolveCliffWalking.py
# 开发工具: PyCharm
"""
1、超参数定义
2、Q-learning策略下的悬崖最优路径规划
   2.1、悬崖创建
   2.2、重置悬崖环境
   2.3、加入路径规划策略
   2.4、训练
   2.5、关闭悬崖环境
3、画图
"""
import random
import numpy as np
import matplotlib.pyplot as plt


# 滑动平均算法
def moving_average(a, n=3):
    ret = np.cumsum(a, dtype=float)
    ret[n:] = ret[n:] - ret[:-n]
    return ret[n - 1:] / n


# 悬崖环境类
class CliffGrid:
    # 初始化悬崖环境参数
    def __init__(self, w=10, h=4, useObstacles=False):
        self.length = w
        self.height = h
        self.useObstacles = useObstacles

        self.action_num = None
        self.init_actions_map()

    # 初始化移动动作及相关参数
    def init_actions_map(self):
        self.act_map = {}
        self.act_map["UP"] = 0
        self.act_map["DOWN"] = 1
        self.act_map["LEFT"] = 2
        self.act_map["RIGHT"] = 3
        self.inv_act_map = {v: k for k, v in self.act_map.items()}
        self.action_num = len(self.act_map)

    # 复制当前网格并返回
    def getObs(self):
        tmp = self.grid.copy()
        tmp[self.agent_loc[0], self.agent_loc[1]] = 2
        return tmp.copy()

    # 获取当前网格状态并输出打印
    def render(self):
        print(self.getObs())

    # 数据类型转换
    def obs2str(self, obs):
        return np.array2string(obs)

    # 生成障碍物位置
    def genObstacles(self, numObstacles, yHigh):
        obstacles = []
        for i in range(0, numObstacles):
            tup = (i + 1, np.random.randint(1, yHigh))
            obstacles.append(tup)
        return obstacles

    # 重置(或重新生成)悬崖环境
    def reset(self):
        # 创建4*10的悬崖网格
        self.grid = np.zeros((self.height, self.length), dtype=np.int32)
        # 对[3,1:9]的位置赋值为1，作为悬崖标志
        self.grid[self.height - 1, 1: self.length - 1] = 1
        # 起点位置
        self.agent_loc = [self.height - 1, 0]
        # 终点位置
        self.goal_loc = [self.height - 1, self.length - 1]

        # 是否对悬崖环境中加入障碍物
        if self.useObstacles:
            # 生成障碍物
            obstacles = self.genObstacles(self.height - 2, self.length - 2)
            # 为悬崖环境添加障碍物
            for obstacle in obstacles:
                self.grid[obstacle[0], obstacle[1]] = 1

        return self.obs2str(self.getObs())

    # 移动策略
    def step(self, action):
        # UP
        if action == 0:
            self.agent_loc[0] -= 1
            if self.agent_loc[0] < 0:
                self.agent_loc[0] = 0
        # DOWN
        elif action == 1:
            self.agent_loc[0] += 1
            if self.agent_loc[0] > self.height - 1:
                self.agent_loc[0] = self.height - 1
        # LEFT
        elif action == 2:
            self.agent_loc[1] -= 1
            if self.agent_loc[1] < 0:
                self.agent_loc[1] = 0
        # RIGHT
        else:
            self.agent_loc[1] += 1
            if self.agent_loc[1] > self.length - 1:
                self.agent_loc[1] = self.length - 1

        # 每正常完成一次移动操作，对奖惩值进行-1
        reward = -1

        # 如果掉入悬崖，则对奖惩值进行-100，并回到初始位置重新开始
        if self.grid[self.agent_loc[0], self.agent_loc[1]] == 1:
            reward = -100
            self.agent_loc = [self.height - 1, 0]

        # 如果到达终点，则将done标志置为True，否则为False
        if self.agent_loc == self.goal_loc:
            done = True
        else:
            done = False

        return (self.obs2str(self.getObs()), reward, done, {})


# Q-learning策略类
class QLearningStrategy:
    def __init__(self, numActs, env, epsilon=0.1, lr=0.01, numIters=10000, discountFactor=0.9, initValue=0.0):
        """
        定义Q-learning决策策略
        :param numActs: 动作数
        :param env: 悬崖环境
        :param epsilon: 贪婪系数
        :param lr: 更新步长
        :param numIters: 迭代次数
        :param discountFactor: 折扣因子
        :param initValue: 初值
        """
        self.initValue = initValue
        self.discountFactor = discountFactor
        self.learningRate = lr
        self.numActs = numActs
        self.numIters = numIters
        self.envObj = env
        self.epsilon = epsilon

    # 创建空的Q表
    def resetDict(self):
        self.qDict = {}

    # 创建动作空间
    def buildDummyActionSpace(self):
        return np.ones(self.numActs).copy() * self.initValue

    # 将创建的动作空间加入Q表中
    def addToDict(self, state):
        if state not in self.qDict.keys():
            self.qDict[state] = self.buildDummyActionSpace()

    # 选取能够使得当前状态Qvector下Q值最大的动作号
    def argmax(self, Qvector):
        if np.count_nonzero(Qvector) == 0:
            action = random.randrange(self.numActs)
        else:
            action = np.argmax(Qvector)
        return action

    # 根据贪婪算法采取动作
    def select_action(self, Qvector):
        if np.random.rand() <= self.epsilon:
            # epsilon randomly choose action
            return random.randrange(self.numActs)
        else:
            # greedily choose action
            return self.argmax(Qvector)

    # 训练
    def learn(self):
        # 创建/重置Q表
        self.resetDict()

        episode = 0
        totalSteps = 0
        self.episodes = []
        self.cumRewards = []
        self.tdErrorList = []
        while totalSteps < self.numIters:
            # 重置悬崖环境
            prevState = self.envObj.reset()
            # 将重置的悬崖环境网格加入Q表
            self.addToDict(prevState)

            cumReward = 0.0
            done = False
            while not done:
                # 根据当前位置选择移动方向
                action = self.select_action(self.qDict[prevState])
                # 由上一步判断的移动方向进行移动
                nextState, reward, done, _ = self.envObj.step(action)
                # 将移动后变化的悬崖环境网格加入Q表
                self.addToDict(nextState)

                # 根据Qlearning算法更新Q表
                bootstrappedTarget = reward + self.discountFactor * np.max(self.qDict[nextState])
                currentEstimate = self.qDict[prevState][action]
                tdError = bootstrappedTarget - currentEstimate
                self.qDict[prevState][action] += self.learningRate * tdError

                # 记录Q表误差及对应的移动奖惩数值
                self.tdErrorList.append(np.absolute(tdError))
                cumReward += reward
                # 记录当前位置
                prevState = nextState
                # 完成一次迭代移动 +1
                totalSteps += 1

                # 如果到达终点，则记录相关信息
                # 并从初始位置重新开始进继续迭代移动
                if done:
                    episode += 1
                    self.episodes.append(episode)
                    self.cumRewards.append(cumReward)
        print("Total States in Q-dict : ", len(self.qDict))

    # 测试
    def execute(self, renderPolicy=False):
        prevState = self.envObj.reset()
        if renderPolicy:
            print("Start State : ")
            self.envObj.render()

        count = 0
        cumReward = 0.0
        done = False
        while not done:
            action = self.argmax(self.qDict[prevState])
            if renderPolicy:
                print("Action : ", self.envObj.inv_act_map[action])
                print('')

            nextState, reward, done, _ = self.envObj.step(action)
            cumReward += reward
            if renderPolicy:
                self.envObj.render()

            prevState = nextState
            count += 1
            if count > 100:
                break

        return cumReward


def main():
    # 1、超参数定义
    grid_w = 10  # 悬崖环境的长
    grid_h = 4  # 悬崖环境的宽

    lr = 0.1  # 更新步长/学习率
    Iters = 100000  # 迭代次数
    epsilon = 0.1  # 贪婪算法的贪婪系数
    discountFactor = 0.5  # 折扣因子 /0.99

    # 是否对悬崖环境添加障碍物，加强模型学习
    Obstacles = False

    # 2、Q-learning策略下的悬崖最优路径规划
    # 加载悬崖
    ClifEnv = CliffGrid(w=grid_w, h=grid_h, useObstacles=Obstacles)
    # 加入路径规划策略
    QLS = QLearningStrategy(numActs=ClifEnv.action_num,
                            env=ClifEnv,
                            epsilon=epsilon,
                            lr=lr,
                            numIters=Iters,
                            discountFactor=discountFactor)

    # 训练Q表
    QLS.learn()

    # 输出训练Q表过程中记录的每轮Q表误差列表
    Errors = QLS.tdErrorList
    # 3、画出每轮Q表的误差曲线
    plt.plot(Errors)
    plt.xlabel("steps")
    plt.ylabel("error in estimates")
    plt.title("Error")
    plt.savefig("Errors.png")
    plt.show()

    # 测试
    QLS.execute(renderPolicy=True)

    Rewards = QLS.cumRewards
    # 3、画出每轮的奖惩值曲线
    plt.plot(Rewards, label="Q-learning")
    plt.xlabel("episodes")
    plt.ylabel("Cum. Reward")
    plt.title("Rewards")
    plt.legend()
    plt.savefig("Rewards.png")
    plt.show()

    # 用滑动平均算法对记录的奖惩值进行平滑处理
    # 使得数据趋势更加明显，易于观察
    RewardsMA = moving_average(QLS.cumRewards, n=200)
    # 3、画出滑动平均后每轮的奖惩值曲线
    plt.plot(RewardsMA, label="Q-learning")
    plt.xlabel("episodes")
    plt.ylabel("Cum. Reward")
    plt.title("Rewards")
    plt.legend()
    plt.savefig("Rewards_MA.png")
    plt.show()


if __name__ == '__main__':
    main()