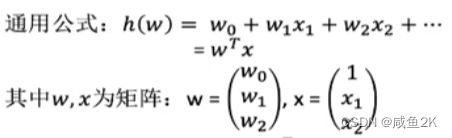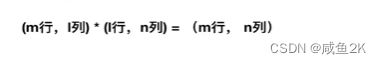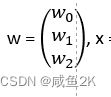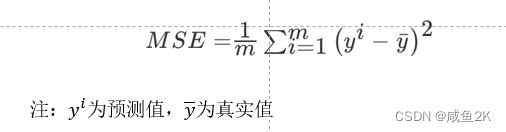机器算法基础——回归分析

内容大纲

 

1、回归算法-线性回归分析

2、线性回归实例

3、回归性能评估

4、分类算法-逻辑回归

5、逻辑回归实例

6、聚类算法-kmeans

7、k-means实例

Q：如何判断是分类算法还是回归算法

由目标值特征来决定使用分类（离散型）算法还是回归（连续型）算法

Q：回归有什么应用分类

回归的应用：一个是知道具体的数据预测，一个是得到回归后的分类问题

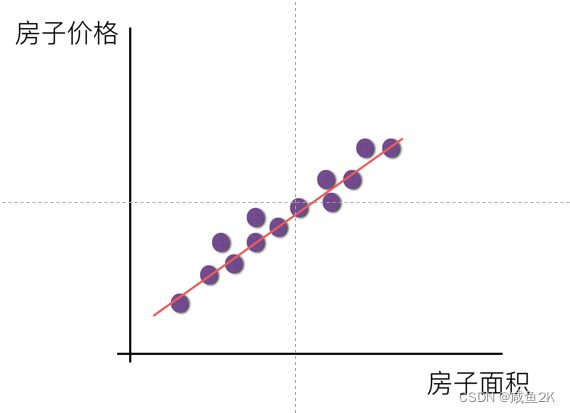
1. 回归算法-线性回归分析

1.1关于线性回归

Q：线性回归的作用

寻找一种能预测的趋势

Q：线性回归特征值与目标值的特点

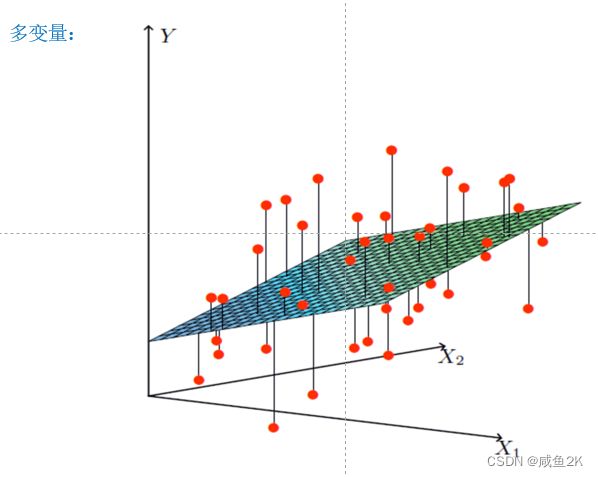
二维：直线关系

三维：平面

1.2关于线性关系模型

Q：概念

一个函数，功能是预测，方式是通过学习属性的线性组合。

 Q：线性回归的定义和对机器算法的对照

定义：线性回归通过一个或者多个自变量（特征值）与因变量（目标值）之间之间进行建模的回归分析。其中特点为一个或多个称为回归系数的模型参数的线性组合

一元线性回归：涉及到的变量（特征值）只有一个

多元线性回归：涉及到的变量（特征值）两个或两个以上

Q：数组的特点

 几维数组就包括有几层括号

N维数组就包括N-1维的数组。

Q：矩阵和数组

矩阵是二维的数组

Q：矩阵为什么在机器算法中非常重要，是大多数算法的基础。以线性回归为例 

 线性回归中用属性和权重的组合来预测结果

矩阵满足特定运算的需求。

矩阵乘法：

 

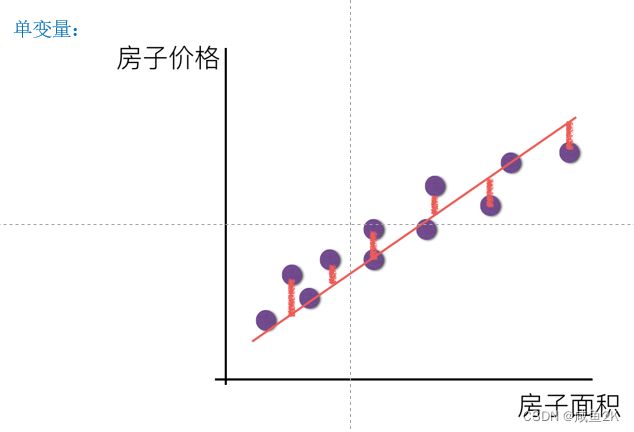
 1.2预测的误差

预测结果和真实值会有偏差

预测与真实的误差 决定了回归与神经网络用的是迭代的算法

通过不断改变权重wi

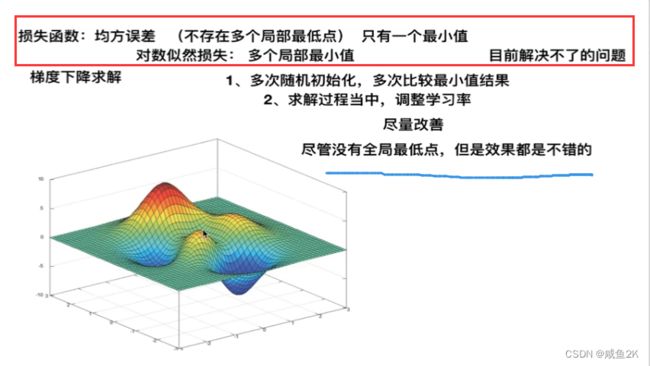
Q：损失函数的概念与内涵

指的是误差大小

 损失 越小，误差越小——找到目标，使总损失最小。

优化的过程，就是不断学习，找到最优的动态权重的过程，

Q：最小二乘法正规方程？

 

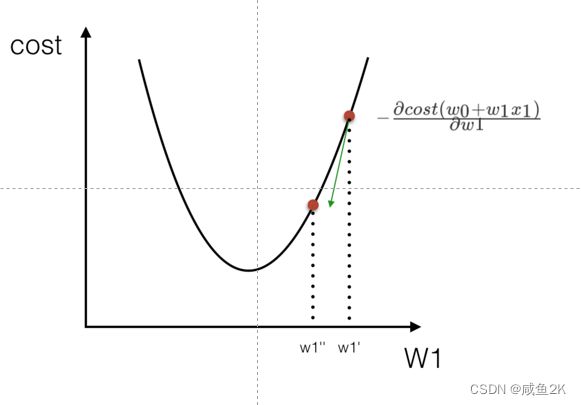
 Q：机器算法：梯度下降（降到最底，底部为损失函数最小）

 a为超参数，手工指定，体现学习调整的速度

方向为系统自带，不用考虑

理解：沿着这个函数下降的方向找，最后就能找到山谷的最低点，然后

更新W值

使用：面对训练数据规模十分庞大的任务

示意图：

 算法的自我学习的过程

 Q：回归API

最终目的是求出W

•sklearn.linear_model.LinearRegression()

• 普通最小二乘线性回归

•

• coef _ ：回归系数

•

•sklearn.linear_model.SGDRegressor( )

• 通过使用 SGD 最小化线性模型

•

• coef _ ： 回归系数

• 梯度下降

Q：sklearn优缺点

 参数在API内部优化，有点像黑盒子

VS~

tensorflow可以自己实现

1.3实例：波士顿房价 

Q：步骤

1、波士顿地区房价数据获取

2、波士顿地区房价数据分割

3、训练与测试数据标准化处理（另一个需要标准化的是K近邻~~~~否则由于二乘法的原因，导致异常。）

特征值和目标值都要标准化处理

（用inverse_transform返回标准化前的处理）

另外特征值和目标值 还不能用同一个标准化实例，因为特征值肯定是多个的，目标值只有一个。

4、使用最简单的线性回归模型LinearRegression和

梯度下降估计SGDRegressor对房价进行预测

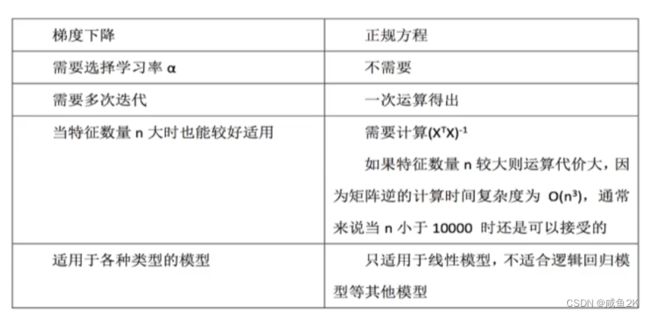
Q：正规方程和梯度下降两种方式的对比

LinearRegression()会有两个版本，两个版本的对比：

from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression, SGDRegressor,  Ridge, LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
def mylinear():
    """
    线性回归直接预测房子价格
    :return: None
    """
    # 获取数据
    lb = load_boston()

    # 分割数据集到训练集和测试集（先特征值再目标值，先训练集再测试集）
    x_train, x_test, y_train, y_test = train_test_split(lb.data, lb.target, test_size=0.25)

    # print(y_train, y_test)

    # 进行标准化处理，特征值 和目标值 都要进行标准化处理，但需要用两个不同的标准化实例
    # 特征值和目标值是都必须进行标准化处理, 实例化两个标准化API
    std_x = StandardScaler()

    x_train = std_x.fit_transform(x_train)
    x_test = std_x.transform(x_test)

    # 目标值
    std_y = StandardScaler()

    y_train = std_y.fit_transform(y_train.reshape(-1, 1))
    y_test = std_y.transform(y_test.reshape(-1, 1))

    # 预测房价结果
    #通过inverse_transform返回标准化之前的值
    y_predict = std_y.inverse_transform(x_test)
    print("保存的模型预测的结果：", y_predict)

    # estimator预测
    # 正规方程求解方式预测结果
    lr = LinearRegression()
    #fit导入训练集中的特征值和目标值
    lr.fit(x_train, y_train)
    #打印特征值的系数
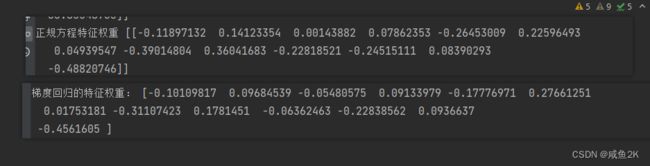
    print('特征权重',lr.coef_)

    # 保存训练好的模型
    # joblib.dump(lr, "./tmp/test.pkl")

    # 预测测试集的房子价格
    y_lr_predict = std_y.inverse_transform(lr.predict(x_test))

    print("正规方程测试集里面每个房子的预测价格：", y_lr_predict)
 
    return None

if __name__ == "__main__":
    mylinear()

Q：正规方程与梯度下降出来的权重是否相同

权重计算出来是不一样的。

Q：回归评价

指标：(均方误差(Mean Squared Error)MSE) 

使用的回归评估API

• sklearn.metrics. mean_squared_error

 解释：

• mean_squared_error ( y_true ,  y_pred )

• 均方误差表示回归损失

参数：

• y_true : 真实值

• y_pred : 预测值

返回值：

• return: 浮点数结果

注：真实值，预测值为标准化之前的值 

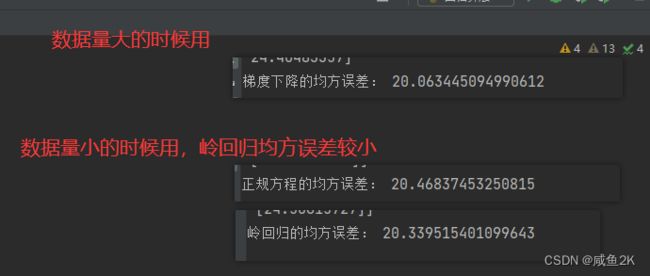
Q：正规方程和梯度下降对于权重的评价

如果数据量小，应当用正规方式，即LinearRegression

如果数据量大，十几万以上时，SGDregression更适合 

官网的推荐：

 再次对比：

Q：对于线性回归的评价

线性回归器是最为简单、易用的回归模型。

从某种程度上限制了使用，尽管如此，在不知道特征之间关系的前提下，我们仍然使用线性回归器作为大多数系统的首要选择。

小规模数据：LinearRegression(不能解决过拟合或者欠拟合的问题)

（有其他的回归算法可以选择）

大规模数据：SGDRegressor

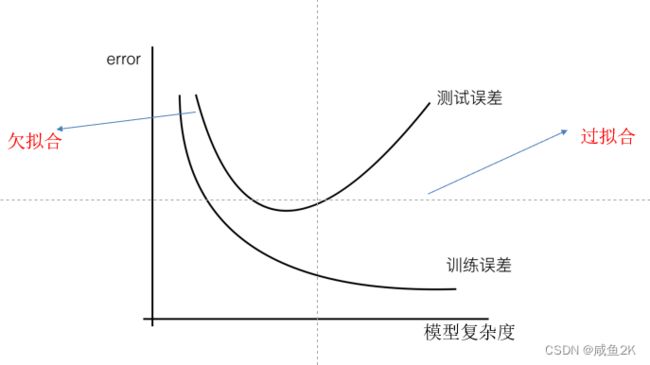
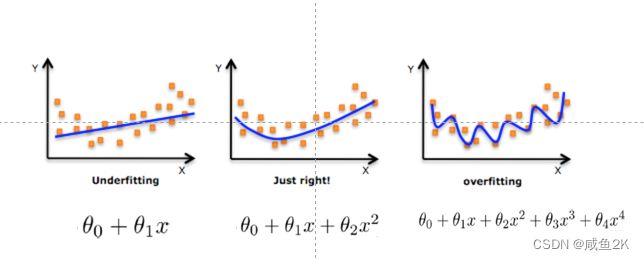
1.4拟合问题

Q：拟合问题

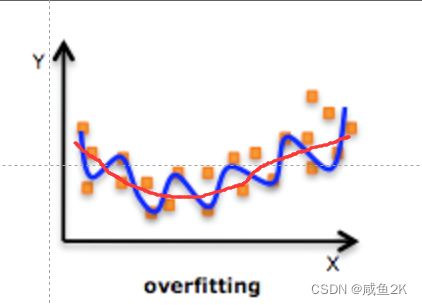
过拟合：一个假设在训练数据上能够获得比其他假设更好的拟合， 但是在训练数据外的数据集上却不能很好地拟合数据，此时认为这个假设出现了过拟合的现象。(模型过于复杂)

欠拟合：一个假设在训练数据上不能获得更好的拟合， 但是在训练数据外的数据集上也不能很好地拟合数据，此时认为这个假设出现了欠拟合的现象。(模型过于简单)

对线性模型进行训练学习会变成复杂模型，主要原因是实际情况中，线性的情况非常少，基本是如下图的情况。但是我们用线性回归分析时，不考虑X，即特征值，只关注权重 。

进而产生欠拟合和过拟合的问题，通过交叉验证的方式进行验证 

 

 Q：对于欠拟合，解决办法

• 原因：

• 学习到数据的特征过少

•

•

• 解决办法：

• 增加数据的特征数量

Q：对于过拟合，解决办法

• 原因：

• 原始特征过多，存在一些嘈杂特征， 模型过于复杂是因为模型尝试去兼顾

各个测试数据点

• 解决办法：

• 进行特征选择，消除关联性大的特征 ( 很难做 )

• 交叉验证 ( 让所有数据都有过训练 )

• 正则化 ( 了解 )

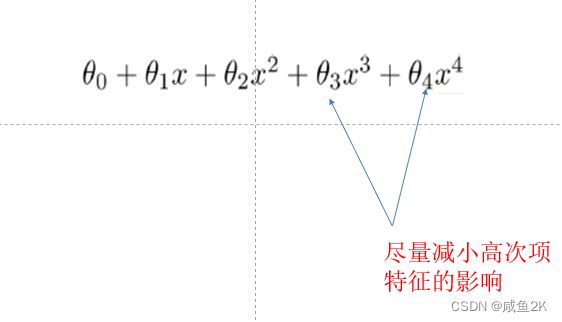
Q：解决过拟合的问题

 权重越小，高次项就越小。

而Lineregression是做不到的，因为线性回归是尽可能的把所有的样本数据都统计进去，并尽可能的精确。

使用如下示意图的方法可以减少高次项权重的目的：

此方法称为：L2正则化

作用：可以使得W的每个元素都很小，都接近于0

优点：越小的参数说明模型越简单，越简单的模型则越不容易产生过拟合现象

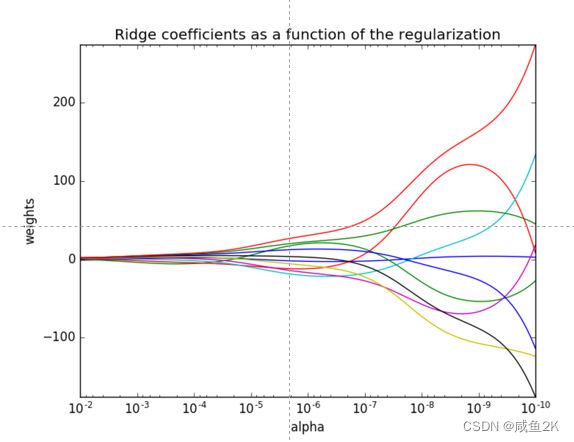
Q：岭回归

 •sklearn.linear_model.Ridge

• sklearn.linear_model.Ridge( alpha=1.0 )

• 具有 l2 正则化的线性最小二乘法

•

• alpha: 正则化力度

• coef _: 回归系数

如下图，从右往左，X轴越大，正则化力度越大，越趋近于0

Q：线性回归和岭回归的对比

• 岭回归：回归得到的 回归系数更符合实际，更可靠 。另外，能让估计参数的波动范围变小，变的更稳定。在存在病态数据偏多的研究中有较大的实用价值。

 

 Q：岭回归的超参数

参照网格搜索，进行调整

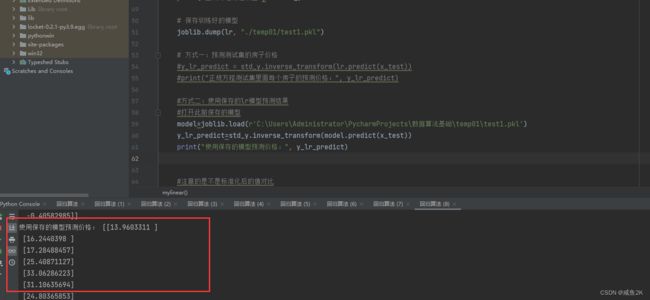
 Q：模型的保存与加载

把自己的模型保存下来，下次使用，或者使用别人已经做好的模型

    import joblib

    # 保存训练好的模型
    joblib.dump(lr, "./temp01/test1.pkl")

    #方式二：使用保存的lr模型预测结果
    #打开此前保存的模型
    model=joblib.load(r'C:\Users\Administrator\PycharmProjects\数据算法基础\temp01\test1.pkl')
    y_lr_predict=std_y.inverse_transform(model.predict(x_test))
    print("使用保存的模型预测价格：", y_lr_predict)

 需要具体说明

（1）pycharm的这个版本中，对于joblib的导入，已经采用

    import joblib，而不再是视频中的例子

（2）保存的模型文件是pkl

保存前必须有相应的路径文件夹，pycharm不会新建文件夹路径

# 保存训练好的模型
joblib.dump(lr, "./temp01/test1.pkl")

 （3）使用时

先通过load加载出来

model=joblib.load(r'C:\Users\Administrator\PycharmProjects\数据算法基础\temp01\test1.pkl')

接下来，通过predict()方法预测，参数为需要进行预测的参数。

y_lr_predict=std_y.inverse_transform(model.predict(x_test))

最后，留意模型预测时，导出的是标准化的值，需要逆转化成业务的实际值。

Q：全部回归代码及解释说明

from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression, SGDRegressor,  Ridge, LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error, classification_report
#from sklearn.externals import joblib
import joblib
import pandas as pd
import numpy as np

def mylinear():
    """
    线性回归直接预测房子价格
    :return: None
    """
    # 获取数据
    lb = load_boston()

    # 分割数据集到训练集和测试集（先特征值再目标值，先训练集再测试集）
    x_train, x_test, y_train, y_test = train_test_split(lb.data, lb.target, test_size=0.25)

    # print(y_train, y_test)

    # 进行标准化处理，特征值 和目标值 都要进行标准化处理，但需要用两个不同的标准化实例
    # 特征值和目标值是都必须进行标准化处理, 实例化两个标准化API
    std_x = StandardScaler()

    x_train = std_x.fit_transform(x_train)
    x_test = std_x.transform(x_test)

    # 目标值
    std_y = StandardScaler()

    y_train = std_y.fit_transform(y_train.reshape(-1, 1))
    y_test = std_y.transform(y_test.reshape(-1, 1))

    #通过inverse_transform返回标准化之前的值
    y_predict = std_y.inverse_transform(x_test)
    print("模型预测的结果：", y_predict)


    # estimator预测
    # 正规方程求解方式预测结果
    lr = LinearRegression()
    #fit导入训练集中的特征值和目标值
    lr.fit(x_train, y_train)
    #打印特征值的系数
    print('正规方程特征权重',lr.coef_)

    # 保存训练好的模型
    joblib.dump(lr, "./temp01/test1.pkl")

    # 方式一：预测测试集的房子价格
    #y_lr_predict = std_y.inverse_transform(lr.predict(x_test))
    #print("正规方程测试集里面每个房子的预测价格：", y_lr_predict)

    #方式二：使用保存的lr模型预测结果
    #打开此前保存的模型
    model=joblib.load(r'C:\Users\Administrator\PycharmProjects\数据算法基础\temp01\test1.pkl')
    y_lr_predict=std_y.inverse_transform(model.predict(x_test))
    print("使用保存的模型预测价格：", y_lr_predict)


    #注意的是不是标准化后的值对比
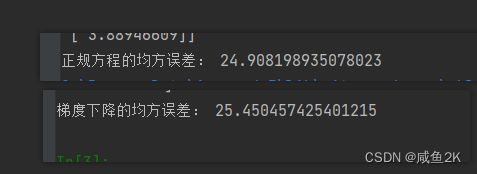
    print("正规方程的均方误差：", mean_squared_error(std_y.inverse_transform(y_test), y_lr_predict))

    # 梯度下降去进行房价预测
    sgd = SGDRegressor()

    sgd.fit(x_train, y_train)

    print('梯度回归的特征权重：',sgd.coef_)

    # 预测测试集的房子价格
    y_sgd_predict = std_y.inverse_transform(sgd.predict(x_test))

    print("梯度下降测试集里面每个房子的预测价格：", y_sgd_predict)
    #注意的是不是标准化后的值 对比
    print("梯度下降的均方误差：", mean_squared_error(std_y.inverse_transform(y_test), y_sgd_predict))

    # 岭回归去进行房价预测
    #alpha为超参数，一般在0~1之间
    rd = Ridge(alpha=1.0)

    rd.fit(x_train, y_train)

    print('岭回归的特征权重',rd.coef_)

    # 预测测试集的房子价格
    y_rd_predict = std_y.inverse_transform(rd.predict(x_test))

    print("岭回归测试集里面每个房子的预测价格：", y_rd_predict)

    print("岭回归的均方误差：", mean_squared_error(std_y.inverse_transform(y_test), y_rd_predict))

    return None

if __name__ == "__main__":
    mylinear()

4.分类算法——逻辑回归

Q：逻辑回归的概念

解决二分类问题：

• 广告点击率

•

• 判断用户的性别

•

• 预测用户是否会购买给定的商品类

•

• 判断一条评论是正面的还是负面的

Q：如何解决

 通过输入线性回归样本数据，得到二分类的概率

输入：h= 0+11+22+…h(w)= w_0+〖w_1 x〗_1+w_2 x_2+…

  = w^T x

（单个样本）

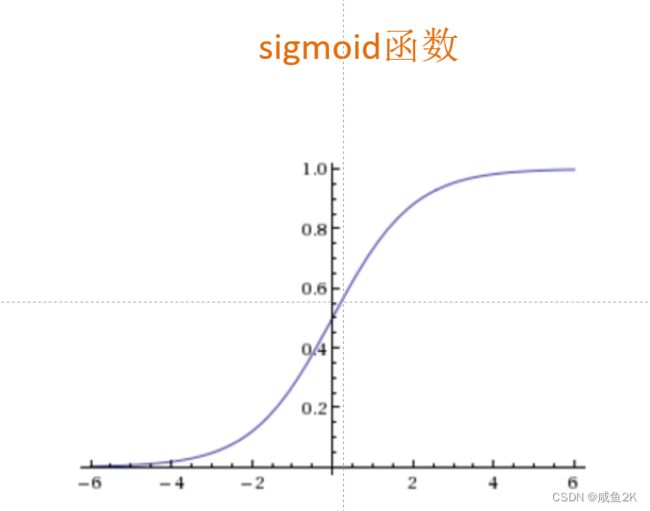
Q：逻辑回归的函数与图形

sigmoid函数是可以转化为0~1的函数

0-1之间可以转化为具体的概率值

Q：逻辑回归的公式

 小于0.5为0，大于0.5为1

Q：逻辑回归的损失函数（了解就好）

也有损失函数

 cost损失的值越小，预测得越好

 

Q：逻辑回归API

• sklearn.linear_model.LogisticRegression ( penalty=‘l2’, C = 1.0 )

•

• Logistic 回归分类器

• coef _ ：回归系数

Q：实例，癌症的检测

完整代码

def logistic():
    """
    逻辑回归做二分类进行癌症预测（根据细胞的属性特征）
    :return: NOne
    """
    # 构造列标签名字
    #如果原来的csv有字段名字，则用构造，如果没有，通过这种方式
    column = ['Sample code number','Clump Thickness', 'Uniformity of Cell Size','Uniformity of Cell Shape','Marginal Adhesion', 'Single Epithelial Cell Size','Bare Nuclei','Bland Chromatin','Normal Nucleoli','Mitoses','Class']

    # 读取数据
    data = pd.read_csv("https://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/breast-cancer-wisconsin.data", names=column)

    print(data)

    # 缺失值进行处理,此处空值是以？的形式出现；删除掉空值
    data = data.replace(to_replace='?', value=np.nan)

    data = data.dropna()

    # 进行数据的分割
    #对列进行切片取数
    x_train, x_test, y_train, y_test = train_test_split(data[column[1:10]], data[column[10]], test_size=0.25)

    # 进行标准化处理，不能让某一特征太突出
    std = StandardScaler()

    x_train = std.fit_transform(x_train)
    x_test = std.transform(x_test)

    # 逻辑回归预测
    #留意c=1.0参数
    lg = LogisticRegression(C=1.0)
    #训练模型
    lg.fit(x_train, y_train)

    print(lg.coef_)

    y_predict = lg.predict(x_test)

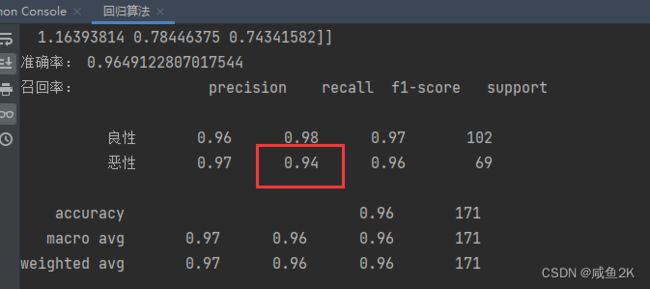
    print("准确率：", lg.score(x_test, y_test))

    print("召回率：", classification_report(y_test, y_predict, labels=[2, 4], target_names=["良性", "恶性"]))

    return None

 CSV读取的问题

• pd.read_csv ( ’’ , names = column_names )

• column_names ：指定类别名字 ,['Sample code number','Clump Thickness', 'Uniformity of Cell Size','Uniformity of Cell Shape','Marginal Adhesion',
                'Single Epithelial Cell Size','Bare Nuclei','Bland Chromatin','Normal Nucleoli','Mitoses','Class ']

• return: 数据

•

• replace( to_replace =’’,value=) ：返回数据

• dropna (): 返回数据

结果：

 

对于当前例子来说，恶性肿瘤的召回率才是重点，准确率没有意义

Q：逻辑回归总结

应用：广告点击率预测、电商购物搭配推荐等二分类的问题

优点：适合需要得到一个分类概率的场景

缺点：当特征空间很大时，逻辑回归的性能不是很好

（看硬件能力）

正则化力度是C=1.0的那个参数

判别模型包括：K-近邻、决策树、随机森林和神经网络等

生成模型学习到的只有朴素贝叶斯

5.非监督学习

K-means 聚类分析

多少个类别为参数，如果不知道参数，则以超参数的形式

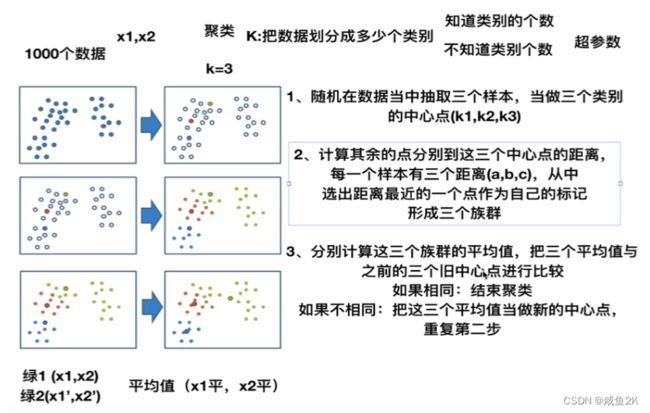
Q：聚类算法的计算过程

 

1、随机设置K个特征空间内的点作为初始的聚类中心

2、对于其他每个点计算到K个中心的距离，未知的点选择最近的一个聚类

中心点作为标记类别

3、接着对着标记的聚类中心之后，重新计算出每个聚类的新中心点（平

均值）

4、如果计算得出的新中心点与原中心点一样，那么结束，否则重新进行

第二步过程

 

 Q：Kmeans的API

• sklearn.cluster. KMeans

• sklearn.cluster.KMeans( n_clusters=8,init=‘k-means++’ )

• k-means 聚类

• n_clusters : 开始的聚类中心数量

• init : 初始化方法，默认为 'k-means ++’

•

• labels_: 默认标记的类型，可以和真实值比较（不是值比较）

 

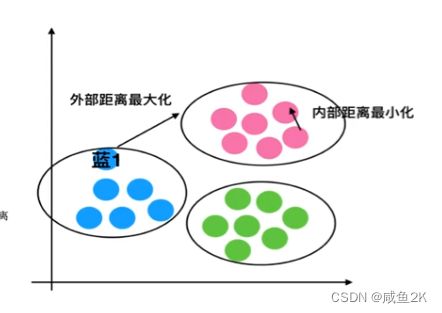
Q:评估：轮廓系数

 

外部距离最大化，内部距离最小化

 

 

如果〖sc〗_i 小于0，说明a_i 的平均距离大于最近的其他簇。

聚类效果不好

如果〖sc〗_i 越大，说明a_i 的平均距离小于最近的其他簇。

聚类效果好

轮廓系数的值是介于 [-1,1] ，越趋近于1代表内聚度和分离度都相对较优

 

Kmeans性能评估指标API 

•sklearn.metrics.silhouette_score

 

• sklearn.metrics.silhouette_score ( X ,  labels )

• 计算所有样本的平均轮廓系数

• X ：特征值

• labels ：被聚类标记的目标值

Q： 实例

F:\学习文件\拜师数据分析学习\3142_机器学习算法基础（基础机器学习课程）\代码和资料\03_机器学习第三天_回归算法、逻辑回归、聚类算法\代码\instacart.ipynb

Q:步骤

总体三步：

1、降维之后的数据

2、k-means聚类

3、聚类结果显示

具体操作：

（1）读取表格

（2）合并表格

_mg = pd.merge(prior, products, on=['product_id', 'product_id'])
_mg = pd.merge(_mg, orders, on=['order_id', 'order_id'])
mt = pd.merge(_mg, aisles, on=['aisle_id', 'aisle_id'])

（3）做成交叉表

# 交叉表（特殊的分组工具）
cross = pd.crosstab(mt['user_id'], mt['aisle'])

（4）主成分分析

原有 134 columns

pca = PCA(n_components=0.9)

data.shape

现有

(206209, 27)

有27个维度

（5）样本数量多，会减少计算机使用性能

# 把样本数量减少
x = data[:600]
x.shape

(600, 27)

（6）训练KMeans模型

km = KMeans(n_clusters=4)

 km.fit(x)

（7）预测

predict = km.predict(x)

（8）绘图

生成一个画布

plt.figure(figsize=(10,10))

#建立四个颜色的列表
colored = ['orange', 'green', 'blue', 'purple']

#生成迭代器
colr = [colored[i] for i in predict]

#所有样本取第一个特征；所有样本取第20个特征
plt.scatter(x[:, 1], x[:, 20], color=colr)

#描述轴

plt.xlabel("1")
plt.ylabel("20")

plt.show()

#评价聚类效果

silhouette_score(x, predict)

看事前是否知道有几种类别，如果不知道则进行超参数处理系数

 Q：