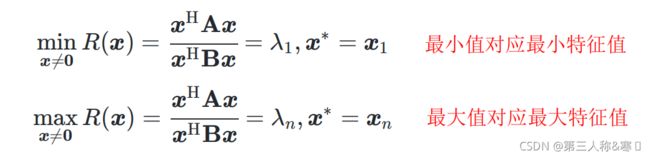机器学习-二分类线性判别分析

目录

前言

一、线性判别分析(LDA)算法原理

 二、损失函数的推导

2.1初步条件推导

2.2最大化目标

三、拉格朗日乘子法求解

3.1拉格朗日乘子法

3.2求解的值

四、拓展定义

4.1广义特征值

4.2广义瑞利熵

总结

---

前言

本文主要记录了有关机器学习问题线性模型中的二分类线性判别分析的内容，思路均来源于周志华老师《机器学习》第三章3.4部分的内容。

---

一、线性判别分析(LDA)算法原理

算法思想:对于给定训练样例集，设法将样例投影到一条直线上，使同类样例尽可能近、异类样例投影尽可能远离；对新样本进行分类时，将其投影到同样的直线上，根据投影点位置来判定类别。

从几何角度上：让全体训练样本经过投影之后，异类样本的中心尽可能远，同类样本的方差尽可能小。

        对于给定的数据集，其中为维的特征向量，为标记，。

        令，，，分别表示第类示例的集合、均值向量、协方差均值，此时表示的取值。以下通过例子解释：

 二、损失函数的推导

2.1初步条件推导

① 经过投影后，异类样本的中心尽可能远（非严格投影）：

投影长度为：，

经过同乘模长，转化为向量内积之差，简化因为存在、带来的计算难度：

等价于：；

 即为： 。

注：二范数=模，对于，，对应  。

 ②经过投影后，同类样本的方差尽可能小（非严格方差）：

       已知两类样本协方差均值为、，对应两类样本协方差分别为：、，若使得同类方差尽可能小，即：；

代入协方差的表达式（乘积项可以省略）：

 等价于：。

2.2最大化目标

综合以上两个方面的优化目标，可以得到欲最大化的目标：，并对其表达形式进行化简：

 令,  ，则上式可转化为：。

由于此时中分母和分子均是关于的二次项，即此式的解与无关，仅仅与其方向有关。

不失一般性，令，则等价于(习惯转化为最小化问题)：

三、拉格朗日乘子法求解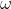

3.1拉格朗日乘子法

       对于仅含等式约束的优化问题：，其中自变量，与均有连续的一阶偏导数。可以列出其拉格朗日函数：

，其中为拉格朗日乘子向量。只要对拉格朗日函数关于求偏导，并令导数等于0再搭配约束条件即可解出，求解出所有的即为上述优化问题所有可能解（对应为极值点处）。

3.2求解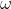的值

 故得到等式：，由于最终要求解的不关心其大小，只关心其方向：

①常数项可以取任意值，如不妨取，则此时可以求解出。

②此处不用严格按照拉格朗日乘子法刻意考虑约束条件。

验证计算出来的价值点是否为最小值点：

由于，故对应目标函数的最大值为0，且必然存在最小值，则对应求解出为最小值对应点。

四、拓展定义

4.1广义特征值

4.2广义瑞利熵

        设，为n阶厄米矩阵，且正定，称 , 为相对于的广义瑞利熵。特别地，当(单位矩阵)时，广义瑞利熵退化为瑞利熵。

厄米矩阵：指矩阵中每一个第行第列的元素都与第行第列的元素的共轭相等，涵盖了虚数范围，对于实数矩阵，等价为转秩矩阵，即,即为对称矩阵。

广义瑞利熵存在以下性质：

       设，为相对于的广义特征值和特征向量，且。

在的前提下，的解记为，存在以下性质：

 在本篇中，最大化目标为及的“广义瑞利熵”。

证明该性质：

和本篇的证明方法相似，当固定时，使用拉格朗日乘子法可推出结论式：这样一个广义特征值的问题，根据其定义，对应的可能解即为这个广义特征向量，将其分别代入即可推出上述结论。

---

总结

以上思路来源于《机器学习》这本书第三章3.4节的内容，二分类线性判别为本书中的重点内容，公式推导过程复杂但不难理解，条理清晰，需要耐心。内容仅代表个人的思路和理解，如有错误欢迎指正！