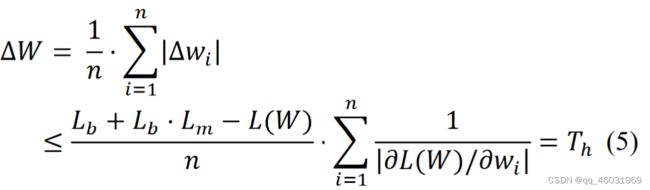论文解读《Structured Pruning for Deep Neural Networks with Adaptive Pruning Rate Derivation Based on Con》

论文：Structured Pruning for Deep Neural Networks with Adaptive Pruning Rate Derivation Based on Connection Sensitivity and Loss Function  基于连接敏感性和损失函数的能够自适应推导剪枝率的深度神经网络结构化剪枝

论文地址：DOI: 10.12720/JAIT.13.3.295-300 

发表时间：2022/6, Journal of Advances in Information Technology（比较新，含金量不确定，题目说得不错）

注：大部分是原文，但不全是，带色的是自己的理解

摘要

结构化剪枝是深度神经网络压缩的一种方式。早期的结构化剪枝手动设置剪枝率（类似于作为超参数存在），因此找到一个合适的能够尽量减少精度损失的剪枝率是很困难的。本文提出了一种基于梯度和损失函数自适应推导各层剪枝率的结构化剪枝方法。该方法首先利用每一层的损失函数和梯度计算出每层修剪权重的一个L1范数阈值，这一阈值能够确保在所剪掉的权重的L1范数小于该阈值时，剪枝不会使损失函数退化。之后，在改变剪枝率时，通过比较所剪掉的权重的L1范数和该阈值，我们能够得到每一层的不使损失函数退化的剪枝率（？这是个什么方法）。在每一层使用我们计算得到的剪枝率，能够抑制剪枝后的模型的精度损失。我们用VGG-16和ResNet在CIFAR-10任务上迭代剪枝评估了所提出的方法。本文方法将ResNet-56的模型参数降低了66.3%，精度为93.71%。（听起来还不错）

I 引言

深度神经网络(DNNs)在分类任务和语义分割等各种任务上都有出色的表现。然而，随着网络性能的提高，DNN模型变得更深更复杂，这一趋势限制了DNN在资源受限设备(如嵌入式系统和移动电话)上的部署。

为了减小DNN模型的大小和计算复杂度而提出了网络剪枝方法。早期方法在给定剪枝率的条件下，删除权重张量中基于某一阈值（这一阈值即由给定的剪枝率决定）下的小权重值。由于这些方法引入了稀疏连接，因此被称为非结构化剪枝。为了降低计算成本，提出了比非结构化剪枝粒度更粗（如通道和神经元，对比于非结构化剪枝中的权重）的结构化剪枝。一些研究中基于每个滤波器的L1范数的值排序来去除通道，或基于group LASSO（不知道是啥），或剪掉那些使输出特征图误差最小化的滤波器（大意是这样，可能目的是让输出特征图和没剪枝时差距最小的意思），或使用剪枝矩阵的梯度作为度量以考虑每一层对整个模型精度的修剪影响。现有的方法都是根据权重值等评估准则和给定的剪枝率来剪枝权重张量。然而，当给定的剪枝率不合适时，剪枝后的模型精度会大大降低。实际应用中使用的网络结构也是多种多样的，因此想要手动确定一个对所有应用都适用的抑制精度降低的剪枝率是非常低效的（一堆废话）。

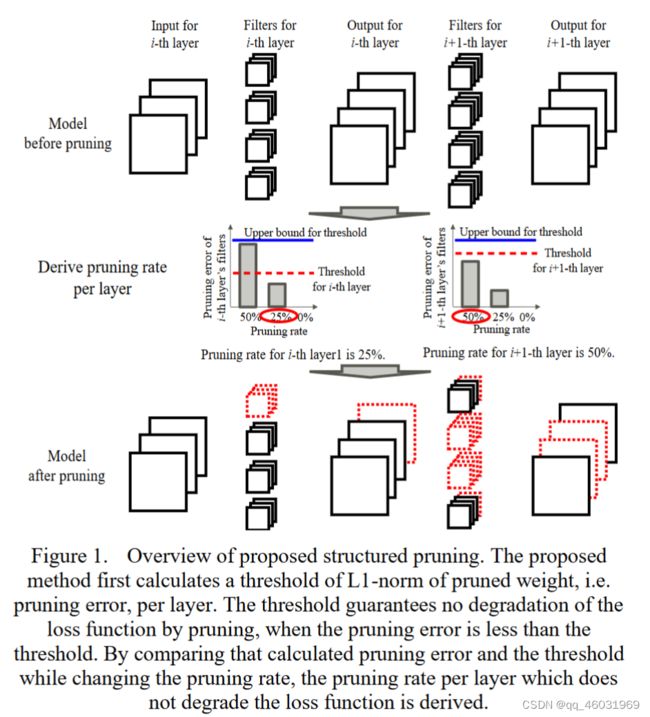
本文提出了一种基于梯度和损失函数自适应推导各层剪枝率的结构化剪枝方法（如图1）。该方法首先使用损失函数和每层的梯度计算每层修剪权重的l1范数阈值（即修剪误差）。当修剪误差小于该阈值时，保证剪枝不会使损失函数退化。在改变剪枝率时，通过比较所剪掉的权重的L1范数和该阈值，我们能够得到每一层的不使损失函数退化的剪枝率。使用我们计算得到的剪枝率，能够抑制剪枝后的模型的精度损失。（哈哈，还是废话）我们在CIFAR-10上用含bn层的VGG-16和ResNet迭代剪枝评估了该方法。该方法使VGG-16模型参数降低了94.4%，精度为93.43%。此外，我们修剪的ResNet-32、ResNet-56和ResNet-100参数分别减少了66.9%、66.3%和84.4%，准确率分别为92.93%、93.71%和93.60%。（原始精度呢？）

本文在结构化剪枝方面的贡献如下：

• 提出了一种结构化的剪枝方法，自适应地推导出每层的剪枝率，通过去除整个模型通道和神经元来压缩网络（虽然不是直接设定剪枝率了，但是是需要一个阈值的，和直接手动设定阈值的差别大概就是每一层的阈值都是由梯度+损失函数算出来的？具体怎么算出来的到现在还没说）

•证明了我们提出的方法可以减少VGG-16, ResNet-32, ResNet-56和ResNet-110在CIFAR-10上的模型参数和浮点运算(FLOPs)的数量，并且没有明显的精度下降。 

II 相关工作

A.重要程度评估准则（以下简称重要程度）（科普废话部分）

结构化剪枝通常以通道等更粗粒度的单位计算重要程度，然后在剪枝率确定的阈值以下对较不重要的通道进行剪枝。权重值广泛用于计算重要程度。特征图映射误差和批量归一化层的比例因子也常用于表示重要程度。然而，这些方法没有考虑网络精度的影响（？何以见得）。虽然[6]使用损失函数的灵敏度如梯度来表示重要程度，但使用灵敏度进行剪枝的表现比使用权重值差。

B.局部剪枝和全局剪枝

重要程度和剪枝率的设置有两种方法。局部剪枝设置重要程度排序和每层剪枝率。由于局部剪枝中剪枝率的组合非常多，因此很难找到抑制精度退化的组合。全局剪枝仅为整个模型设置一个剪枝率，并计算整个模型的重要程度排序。因此在全局剪枝中，每层剪枝率一般是不同的。

C.Pruning Scheduling（不知道咋翻译）

为了抑制剪枝导致的精度下降，通常对剪枝后的模型微调。One-shot 剪枝只对模型进行一次高剪枝率的剪枝，然后微调剪枝后的模型。迭代剪枝以较低的剪枝率迭代执行对模型的剪枝过程并微调。早期研究已经说明迭代剪枝的精度退化小于One-shot剪枝。我们提出的方法得到了每一层的剪枝率（类似于局部剪枝），而每层的最终剪枝率与全局剪枝相似（其实就是每层设置不一样的剪枝率的局部剪枝吧）。这是因为所提出的方法根据每一层的梯度自适应地推导出每层的剪枝率。该方法使用梯度来推导剪枝率，以考虑剪枝对损失函数的影响。为了抑制剪枝对精度的影响，该方法采用迭代剪枝，使用权重值作为重要程度。

III 方法

我们提出的剪枝方法流程如Alorithm 1所示，该方法对预训练模型进行剪枝。首先推导出剪枝率（你还是没说咋推导的），并利用得到的剪枝率对模型进行剪枝。在对剪枝后模型进行微调后，通过比较微调模型和预训练模型的精度来决定是否采用所得到的剪枝率（？为啥还需要决定是否采用）。迭代执行剪枝率推导、模型剪枝、微调和精度比较过程，直到所有层的剪枝率都选择为0%。

A.剪枝率推导

理想剪枝率可以防止剪枝导致的精度下降（真理想啊）。如果得到理想剪枝率，则期望由理想剪枝率剪枝的模型的损失函数也没有退化。我们从这个理想情况出发设定了以下约束条件。由剪枝后模型导出的损失函数小于或等于由剪枝前模型导出的损失函数。当只去除一个包含剪枝目标张量的元素时，上述约束如(1)所示。

其中是修剪目标张量的第i个元素。i= 1,2,……，n为元素的索引。N是这个张量的元素个数。∆=−为剪枝误差，即第i个元素剪枝前后权值的差值。L(1 +∆1，2，⋯，)为修剪后模型的损失函数，Lb为修剪前模型的损失函数。将一阶泰勒展开应用于修剪模型的损失函数，我们可以得到(2)

 式中，。由于L(W)的值与Lb的值相同，(2)不能满足。为了满足(2)，我们通过引入边际损失函数（这是啥）来放松约束。由剪枝后模型导出的损失函数小于或等于“带边缘”的由剪枝前模型导出的损失函数。我们根据松弛约束对(2)进行了修改。

 式中Lb⋅Lm是松弛约束引入的损失函数的裕度，Lm是损失函数裕度的控制参数。虽然Lm是超参数，但由于本文方法最终得到的剪枝率是通过精度比较确定的，因此最终得到的剪枝率相对于Lm具有鲁棒性。我们在实验中看到了对Lm的鲁棒性(第4节)。(3)式得到了剪枝误差的上界∆1，满足以下约束条件：

 利用(4)式，我们可以根据损失函数的退化来决定1是否可以被修剪。我们将(4)扩展到(5)以进行更粗粒度的剪枝，如通道剪枝。

 (5)式左侧ΔW为按元素数量归一化的修剪权重的l1范数，即ΔW为粗粒度计算的修剪误差。在修剪一个张量时，由于被剪枝的权重的个数由剪枝率决定，因此被剪枝的权重l1范数的值取决于剪枝率。(5)右侧为剪枝误差的上界，即阈值Th，与剪枝率无关。此外，由于梯度是每层独立推导的，阈值Th也是每层独立推导的。因此，利用(5)式可以通过以下方法为每一层独立找到抑制损失函数退化的剪枝率：设置候选剪枝率Ratecand（最终剪枝率还是人为设定的，提供一系列值然后由算法找到其中最适合的），并从候选剪枝率中找到一个剪枝率，使得修剪误差ΔW小于或等于阈值Th。

迭代剪枝是抑制剪枝导致的精度下降的一种方法。该方法利用(5)得到的剪枝率对模型进行迭代剪枝，并对剪枝后的模型进行微调。式(6)给出了迭代剪枝k次的阈值:Th,k。

 其中Wk是搜索剪枝率k次后的修剪后模型的权重张量。当k=0时，由于尚未求出剪枝率，W0与剪枝前模型的权值张量相同。在Algorithm 2所示的剪枝率推导方法中，可以通过计算滤波器和神经元层面上的剪枝误差和阈值来推导结构化剪枝的剪枝率。此外，该方法还可以在单个权重层面计算非结构化剪枝的剪枝率。

由于阈值Th,k包含由泰勒展开得到的近似误差，存在由(6)得到的修剪速率不正确的可能性。为了减少近似误差的影响，我们引入了信赖域法（暂时不知道是啥），这是一种利用包含误差的参数进行优化的方法。在使用信任域方法时，为了避免由于误差而导致的不正确优化，设置了一个上界，称为信任半径，它限制了包含误差的参数的值。在我们提出的方法中，所有层的阈值由(7)所示的Ub限制。

 其中Th,k,all = [Th,k,1, Th,k,2，…Th,k,m]是阈值的向量，m表示剪枝目标张量的个数。Th,k,i (i=1,2，…，m)是每个修剪目标张量的阈值。

B.模型剪枝与微调

在得到剪枝率后，根据所得到的剪枝率修剪模型。修剪重要程度为权值的l1范数。在给定剪枝率确定的阈值以下的权重将被删除。在微调中，剪枝后模型使用最新微调模型的权重。在第一次搜索的情况下，剪枝后模型使用预训练模型的权重。

C.精度比较

为了抑制剪枝模型的精度退化，达到预期的精度，对修剪模型进行微调，直到剪枝模型精度Accp加上精度控制参数Accctrl超过预训练模型的精度Accb。当Accp+Accctrl超过Accb时，采用推导出的剪枝率。当Accp+Accctrl不超过Accb时，导出的剪枝率被丢弃（相当于回到了剪枝前的上一步？）。迭代执行信赖域方法时，由于上界影响优化的收敛性，每次迭代都会根据优化结果更新上界，上界限制包含误差的参数值。在该方法中，当Accp+Accctrl超过Accb时，Ub上限增大，而当Accp+Accctrl不超过Accb时，Ub上限减小。

D.剪枝搜索终止条件

该方法迭代执行剪枝率推导、模型剪枝、微调和精度比较，直到所有层的剪枝率选择为0%。

E.设置阈值上界（比较有用）

当的上界初始值较小时，阈值在第一次搜索也会被设置为较小值，此时存在所有层的剪枝为0%的可能性，使剪枝率搜索在第一次搜索时终止。为避免第一次搜索时终止，将的初始值设为剪枝率候选Ratecand的最大剪枝率下各层修剪误差的l2范数。由式(7)可知，当设为l2范数时，保证了各层修剪率选择的自由度。

本文方法根据精度比较结果，将的上限更新为较大的值。但是，当Ub值极大时，优化的收敛时间较长。我们将的初始值设为上限的上限。（好吧）

F.修剪shortcut connection

带有concatenate block的shortcut connection通常用于ResNet等深度神经网络。对于一个concatenate block，多个输入特征映射的数量必须相等。为了对齐输入特征映射的数量，我们只修剪那些在所有层上修剪了相同索引的滤波器，如图2所示。（即对于被concatenate的层只修剪在这几个层里都被认为该修剪的滤波器，即取交集）

IV 实验

我们使用带bn层的VGG-16、ResNet-32、ResNet-56和ResNet-110在CIFAR10上评估了所提出的方法。我们使用Kim的VGG-16预训练模型[15]，Idelbayev的ResNet预训练模型[16]。候选剪枝率分别为10%和0%（只需要两个就可以吗？是怕多了搜索不过来吗）。采用L2权值衰减的动量SGD对评价模型进行再训练。mini-batch大小为128。动量系数为0.9。重量衰减系数为10-4。重训练时间为300个epoch。初始学习率为0.1。学习率在第100、150和200代乘以0.1。我们在Pytorch上实现了所提出的方法。代码见https://github.com/FujitsuLaboratories/CAC/tree/main/cac/pruning.

A.超参数性能

图3(a)显示了VGG16剪枝后模型性能与损失边际控制参数Lm的关系。当Lm为0时，压缩比变为0%。每一层的初始阈值也变为0。因此，在第一次搜索时，所有搜索的剪枝率变为0%。当Lm大于0时，Lm的选择对压缩比影响不大，说明了Lm选择的鲁棒性。以下实验中选取Lm = 0.1。

B.剪枝率搜索的性能

图3(b)显示了VGG16剪枝后模型性能与精度控制参数Accctrl的关系。由于对于所有Accctrl值，剪枝后模型精度均大于预训练模型精度减去Accctrl的值，因此该方法可以通过Accctrl控制修剪模型精度。结果是，压缩比随着精度的降低而增加，这与直觉和早期研究[12]，[14]一致。

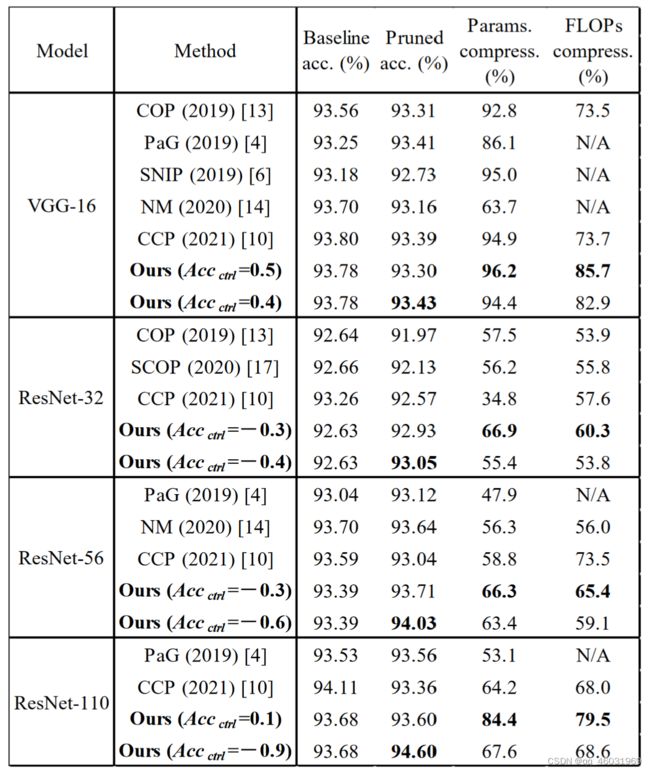
C.性能对比

Table 1列出了与以往工作的比较。结果表明，该方法对所有评估模型在相似的修剪模型精度下都能获得最佳的参数压缩率和FLOPs。此外，我们修剪的ResNet-56和ResNet-110在相似的参数压缩比下达到了显著的修剪模型精度，分别为94.03%和94.60%。

V 结论

本文提出了一种具有自适应剪枝率推导的结构化剪枝方法。为了抑制剪枝对精度的影响，根据每一层的梯度和整个模型损失函数，推导出每一层的剪枝率。通过将所提出的剪枝方法应用于VGG-16、ResNet-32、ResNet-56和ResNet110，剪枝模型的参数和flop可以显著降低，且精度没有明显下降。在未来的工作中，我们将把提出的方法应用于其他任务和模型，如ImageNet[17]、transformer[18]和BERT[19]。