Python绘制地磁场

简介

pyIGRF为国际参考磁场对Python的封装，可通过经纬高度以及时间来计算地磁场强度，使用方法简单粗暴，如下

import pyIGRF
pyIGRF.igrf_value(lat, lon, alt, date)

参数含义为

• lat 纬度
• lon 经度
• alt 海拔
• date 日期，输入四位十进制整数表示年份

其返回值有七个，若写成

D, I, H, X, Y, Z, F = pyIGRF.igrf_value(lat, lon, alt, date)

各返回值含义为

• D 偏角，以东向为正
• I 倾角，以竖直向下为正
• H 水平强度
• X 北向分量
• Y 东向分量
• Z 垂直分量，以下方为正
• F 总磁场强度

角度采取角度制， 磁场强度单位为nT。

通过函数pyIGRF.igrf_variation可以获取磁场的变化情况，其输入与igrf_value相同，输出量的物理量也相同，但代表的是年变化量。

磁场绘制

接下来绘制一下某片区域的磁场分布，令经度范围在126附近，纬度范围在46附近，海拔由0到3000米。

地球建模采取WGS84，其长半轴为6378137km，扁率$e=\frac{1}{298.257223563}$，则短半轴为b = 6356752.314m。

import numpy as np
import matplotlib.pyplot as plt
xs, ys, zs = np.indices([5,5,5])
xs = (xs/500 + 125).flatten()
ys = (ys/500 + 45).flatten()
zs = (zs*600).flatten()
vals = [pyIGRF.igrf_value(y, x, z, 2022) 
    for x,y,z in zip(xs,ys,zs)]
vals = np.array(vals)
Hx, Hy, Hz, H = vals[:,3:].T

LAT = 6356752.314*np.pi/180
xs = (xs-np.min(xs))*np.sin(np.deg2rad(ys))*LAT
ys = (ys-np.min(ys))*LAT

ax = plt.subplot(projection='3d')
ax.quiver(xs, ys, zs, Hx/300, Hy/300, Hz/300)
plt.show()

最终效果如图所示，可见随着高度的增加，地磁场是逐渐减弱的。

接下来可以查看某地随着高度变化，其地磁场分量的变化

hs = np.arange(10000)
vals = [pyIGRF.igrf_value(46, 125, h, 2022) 
    for h in hs]
vals = np.array(vals).T
labels = ["North", "East", "up"]
for i in range(3):
    plt.plot(hs, vals[i+3], label=labels[i])

plt.legend()
plt.show()

结果为

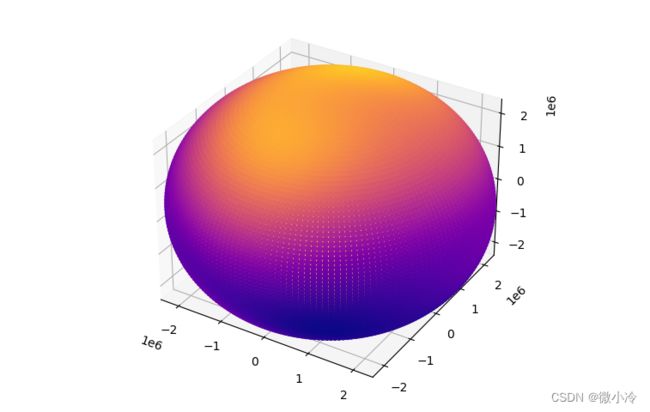
当然，这一局部地磁场分布其实看不出什么，接下来绘制一下全球的磁场分布情况

Ls, Bs = np.indices([180,90])
Ls = (Ls*2 - 180).flatten()
Bs = (Bs*2 - 90).flatten()
vals = [pyIGRF.igrf_value(y, x, 100, 2022) 
    for x,y in zip(Ls,Bs)]
vals = np.array(vals).T
H = vals[-1]

r = 6356752.314/2
Bs, Ls = np.deg2rad(Bs), np.deg2rad(Ls)
xs = r*np.cos(Bs)*np.cos(Ls)
ys = r*np.cos(Bs)*np.sin(Ls)
zs = r*np.sin(Bs)

ax = plt.subplot(projection='3d')
cax = ax.scatter(xs, ys, zs, c=H, cmap='plasma')
plt.show()

效果如图所示