【数学建模】python实现差分进化算法
没找到python代码,自己写了点。(莫非太简单了)
放上github开源网址
github:差分进化
参考教程:优化算法笔记(七)
讲真,这位大佬是真的厉害ww
差分进化算法(Differential Evolution Algorithm,DE)是一种高效的全局优化算法,也是智能优化算法中由种群进化启发的算法之一(智能优化算法笔记)。它也是基于群体的启发式搜索算法,群中的每个个体对应一个解向量。差分进化算法的进化流程则与遗传算法非常类似,都包括变异、杂交和选择操作,但这些操作的具体定义与遗传算法有所不同。
差分进化算法(Differential Evolution,DE)由Storn和Price于1995年首次提出。主要用于求解实数优化问题。该算法是一类基于群体的自适应全局优化算法,属于演化算法的一种,由于其具有结构简单、容易实现、收敛快速、鲁棒性强等特点,因而被广泛应用在数据挖掘、模式识别、数字滤波器设计、人工神经网络、电磁学等各个领域。1996年在日本名古屋举行的第一届国际演化计算(ICEO)竞赛中,差分进化算法被证明是速度最快的进化算法。
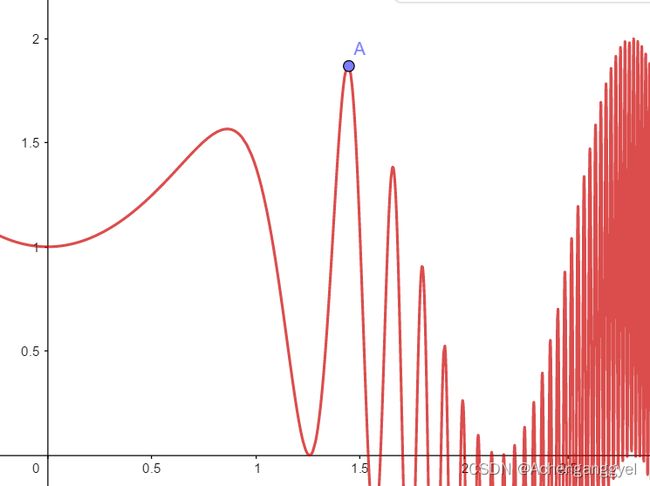
这里也放下代码——以max = sin(x^2)+cos(x^5)为例,我们想知道[1,2]上最大值A的横坐标值。
p.s. 如果是min,适应度函数乘以-1即可。
p.p.s. 很多感叹号的地方,代表修改代码以适应其他情况时,这些地方要改动。
import numpy as np
import pandas as pd
import random
import math
import matplotlib.pyplot as plt
# Places with dense exclamation marks indicate that you need to delete them when you use them
单独放适应度计算CalFitness函数,方便其他情况下计算的修改。特别注意,列表x是单次迭代过程的一个个体的所有基因
def CalFitness(x=[]): #fitness function calculation
#!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
return math.sin(pow(x[0],2))+math.cos(pow(x[0],5))
然后写种群进化的主要过程,变异、交叉和选择。输入和输出可以翻译下我用蹩脚英语写的注释(遁
'''
the base of differential evolution
@args:
cross_rate: the rate of genetic crossover
F: the shrinkage factor. The large the 'F', the slower the convergence speed. usually in [0,2]
gen: generation. The number of iterations
init_N: initial population, will not change. usually in [30,50]
num_x: the number of arguments(decision variables)
bounds: ranges of independent variables,[[x1_lower bound,x1_upper bound],[x2_lower bound,x2_upper bound], ...]
@return:
colony: final result. Convergence if all values are alike
best_scores: The maximal fitness value in each iteration
'''
def DE_base(cross_rate = 0,F = 0.5, gen = 10, init_n = 30, num_x = 1, bounds =[[]]):
best_scores = []
#initialize GENES of the COLONY
colony = []
for i in range(init_n):
colony.append([random.uniform(bounds[x][0],bounds[x][1]) for x in range(num_x)]) #uniform-float, randint(lower_bounds,upper_bounds)-int
#!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
colony = np.array(colony)
#start iteration
for i in range(gen):
b_score = CalFitness(colony[0])
# iteration
for j in range(init_n):
# variation
parents = random.sample(range(init_n),3) #pick 3 randomly from the current population
new = colony[parents[0]]+F*(colony[parents[1]]-colony[parents[2]])
# cross
d_rand = random.randint(0,num_x) #ensure that at least one gene will change
for k in range(num_x):
if random.random()>=cross_rate and k != d_rand:
new[k] = colony[j][k] #restore the orginal gene
# select: greedy algorithm retains the optimal individuals
if CalFitness(new) > CalFitness(colony[j]):
colony[j] = new # update individual
tmp_score = CalFitness(colony[j])
# update [best_scores]
if tmp_score > b_score:
b_score = tmp_score
best_scores.append(b_score)
return colony,best_scores
之后,之后做迭代次数和适应度函数的关系图。这里没用英文注释是因为懒得翻译了(老实巴交.jpg)
'''
drawing function
'''
def drawProcess(best_scores = []): #绘制得分(适应度函数)变化曲线
#绘图时显示中文
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
#设置图像大小
plt.rcParams['figure.figsize'] = (13.0, 10.0)
plt.subplot(111)
plt.plot(best_scores, color = '#2b73af', linewidth = 3)
plt.xlabel('迭代次数',fontsize = 20,verticalalignment = 'baseline',labelpad = 10)
plt.ylabel('适应度函数值',fontsize = 20,verticalalignment = 'bottom',labelpad = 10)
plt.tick_params(labelsize=20,pad =0.3) # 刻度轴
plt.savefig('./optimal/scores.png')
最后,最后!调用以上函数
ans,best_scores_global = DE_base(cross_rate = 0.70,gen = 30,bounds=[[1,2]])
print('最终结果:',ans)
print('迭代中适应度函数:', best_scores_global)
drawProcess(best_scores_global)
当-当-当!结果出现了!
适应度函数最大值,即目标函数在1.44123附近使目标函数取最大值,且目标函数最大为1.836

迭代次数-适应度值图如下。可以看出此函数较简单,仅10次左右算法即可收敛

并没有结束~用lingo验证下结果
一致,没问题,完美,收工 [over.jpg]