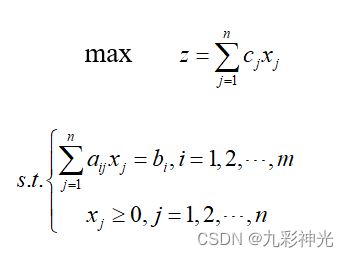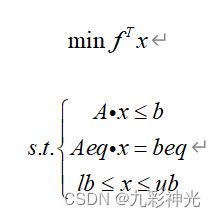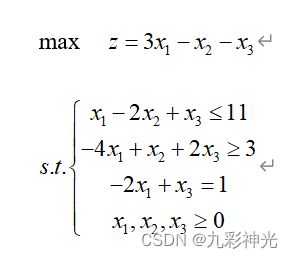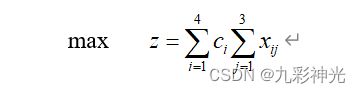Matlab线性规划
1.基本原理
一般线性规划问题的数学标准型为
满足约束条件的解，称为可行解，使目标函数达到最大值的可行解称为最优解。所有可行解构成的集合称为问题的可行域。
Matlab中规定线性规划的标准形式为
式中：f,x,b，beq,lb,ub为列向量，其中f称为价值向量，b称为资源向量，A，Aeq为矩阵。
Matlab中求解线性规划的命令为
[x,fval]=linprog(f,A,b)
[x,fval]=linprog(f,A,b,Aeq,beq)
[x,fval]=linprog(f,A,b,Aeq,beq,lb,ub)
其中：x返回决策向量的取值，fval返回目标函数的最优值，A和b对应线性不等约束；Aeq和beq对应线性等式约束；lb和ub分别对应x的下界向量和上界向量。
2.案例分析
例1 使用Matlab软件求解下列线性规划问题。
Matlab代码：
f=[-3;1;1];
a=[1,-2,1;4,-1,-2];
b=[11,-3];
aeq=[-2,0,1];
beq=1;
[x,y]=linprog(f,a,b,aeq,beq,zeros(3,1));
x,y=-y求解结果为：
x1=4,x2=1,x3=9,z的最大值为2。
例2 一架货机有三个货舱：前舱、中仓和后舱。三个货舱所能装载的货物的最大重量和体积有限制如表5所示。并且为了飞机的平衡，三个货舱装载的货物重量必须与其最大的容许量成比例。
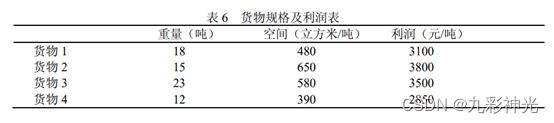
现有四类货物用该货机进行装运，货物的规格以及装运后获得的利润如表6所示：
假设：
（1）每种货物可以无限细分；
（2）每种货物可以分布在一个或者多个货舱内；
（3）不同的货物可以放在同一个货舱内，并且可以保证不留空隙。 问应如何装运，使货机飞行利润最大？
解：用
=1,2,3,4分别表示货物1，货物2，货物3和货物4；
=1,2,3分别表示前舱、中舱和后舱。设
表示第i种货物装在第j个货舱内的重量，
分别表示第j个舱的重量限制和体积限制，
分别表示可以运输的第i种货物的重量，单位重量所占的空间和单位货物的利润，则目标函数为
约束条件为
Matlab代码：
clc,clear
c=[3100;3800;3500;2850];
c=c*ones(1,3);
c=c(:);%把矩阵转化成一列
a1=zeros(4,12);
for i=1:4
a1(i,i:4:12)=1;
end
b1=[18;15;23;12];
a2=zeros(3,12);
for i=1:3
a2(i,4*i-3:4*i)=1;
end
b2=[10;16;8];
a3=zeros(3,12);
bb=[480;650;580;390];
for j=1:3
a3(j,4*j-3:4*j)=bb;
end
b3=[6800;8700;5300];
a=[a1;a2;a3];b=[b1;b2;b3];
aeq=zeros(2,12);
aeq(1,1:4)=1/10;
aeq(1,5:8)=-1/16;
aeq(2,5:8)=1/16;
aeq(2,9:12)=-1/8;
beq=zeros(2,1);
[x,y]=linprog(-c,a,b,aeq,beq,zeros(12,1));
x=reshape(x,[4,3])
x=sum(x'),y=-y利用Matlab求解得到每个货舱存放每种货物的结果如下
即四种货物的吨数分别为0t,15t,15.9474t,3.0526t，总利润为121520元。