基于分支限界的0-1背包问题

一、实验目的

1.掌握基于分支限界的算法求解0-1背包问题的原理和编写分支限界函数的具体步骤。

2.掌握分支限界法的基本思想并通过求解0-1背包问题体会使用优先队列分支限界的方法，从而理解分支限界算法的基本求解过程。

3.体会分支限界算法求解问题的便利和所编写程序的明确结构和良好的可读性。

4.具备运用分支限界算法的思想设计算法并用于求解其他实际应用问题的能力。

5.从算法设计分析角度，对比学习分支限界法求解问题与回溯法求解问题的不同思路，从而对0-1背包问题基于分支限界法求解有更进一步的理解。

二、实验环境

操作系统：Windows 10

文本编辑器：Visual Studio Code

实验语言和编译器：C++

编译器：gcc 8.1.0

实验终端：Windows PowerShell

三、实验内容

现在给定N个物品，每个物品的重量为w（即物品i的重量为wi），给定一个背包，背包的容量为c，0-1背包问题要解决的是，通过选择装入背包中的物品，使得所选择物品的重量之和w在小于等于背包容量的情况下，使得装入背包的物品的价值为所有选择之中最大的那个。

0-1背包问题有如下限制，对于每种物品i，有两种选择，装入或不装如（装入为1，不进行装入为0），既不能装入多次，也不能只装入一部分。

I	1	2	3	4
W(重量)	3	5	2	1
P（价值）	9	10	7	4

    例如若当前背包容量为9，有4个物体，各个物体的重量和价值如上图所示:则通过分析可知，最优解为装入价值为9，10，4的物品，最优价值为23，下面将通过回溯算法实现求解该01背包问题。

程序输入，首先输入物品的数量n和背包的容量c，并依次输入n个物品的重量wi和每个物品的价值pi，程序要求输出为可以得到的最优价值和达到最优值所装入的物品序号。

四、算法描述

通过分析问题可知，0-1背包问题为整数线性规划中的01规划问题

对于回溯算法，将这n个物品装入背包，每个物品对应两个状态，装入背包或不装入背包。第i中物品对应（x1，x2，…，xn），其中xi可以取0或1，分别表示将该物品装入背包或不装入背包。解空间有2^n种可能的解法，也就是n个元素组成的集合所有子集的个数，该集合可以采用一棵满二叉树将该解空间组织起来，解空间的深度为问题的规模n。

使用优先队列式分支限界法求解0-1背包问题搜索解空间的策略是，在扩展结点处（对应代码中E），先生成其所有的儿子节点（分支），再从当前的优先队列中选择下一个扩展结点，为了加速搜索的过程，在每个活结点处都先计算一个函数值（限界，使用Bound函数实现），并根据函数值从优先队列中选择最优的结点作为扩展结点，使得搜索朝着解空间中有最优解的分支前进，增加搜索的速度。

在优先队列的实现中，物品由结构体obj表示，结构体中的成员p表示物品的价值，成员w表示物品的重量，double成员pDivW表示物品的单位价值。

算法从根节点开始搜索，初始时优先队列为空（最大堆为空），取出优先队列中的首元素成为当前的扩展结点E，并将扩展结点的左右儿子设为可行结点加入到优先队列中，优先队列中的结点元素的优先级由Bound函数计算给出，结点元素由结构体node表示，结点元素中使用up表示结点的价值上界，profit和weight表示结点相应的价值和重量，使用变量level表示结点元素在子集树中对应的层序号，使用node指针parent指向该节点在子集树中的父结点。

寻找最优解的过程中，可以使用剪枝函数来加速搜索。bound函数给出每个可行结点对应的子树可能获得的最大价值的上界，若这个上界不会比当前最优值大，则可以剪去该枝（因为相应的子树中不含问题的最优解）。

算法（MaxKnapSack）开始搜索前，使用sort按单位价值对obj结构体数组objs按单位价值非递增排序。E表示当前扩展结点，cw为扩展结点对应的重量，cp对应结点的价值，up表示当前的价值上界。搜索过程如下：

①：初始化优先队列q（使用stl中priority_queue实现，优先队列的排序使用仿函数实现），扩展结点E，初始化变量cw，cp为0。

②：给当前最优值bestp赋0，价值上界up的值为Bound（1）。

③：while循环内部不断扩展结点，直到子集树的叶节点成为扩展结点为止。首先判断当前扩展结点的左儿子，若左儿子为可行结点，调用AddAliveNode将左儿子结点加入优先队列中。

④：更新up值为Bound(i+1)并检查当前扩展结点的右儿子结点，若up≥bestp，说明右子树可能包含最优解，调用AddAliveNode将右儿子结点加入优先队列中。

⑤：从优先队列中取下一结点，继续循环。循环结束后构造当前最优解。

代码逻辑如下：

    priority_queue, cmp > q; // 大顶堆

    node *E = NULL;

    cw = 0;

    cp = 0;

    bestp = 0;

    int i = 1;

    int up = Bound(1);

    //搜索子集空间树

    while(i != n + 1)

    {

        //检查当前扩展结点的左儿子

        int wt = cw + objs[i].w;

        //若左儿子结点为可行结点

        if(wt <= c)

        {

            if(bestp < cp + objs[i].p)

                bestp = cp + objs[i].p;

           AddAliveNode(q, E, up, cw + objs[i].w, cp + objs[i].p, i, 1);

        }

        up = Bound(i + 1);

        if(up >= bestp)

        {

            AddAliveNode(q, E, up, cw, cp, i, 0);

        }

        E = q.top();

        q.pop();

        cw = E->weight;

        cp = E->profit;

        up = E->up;

        i = E->level;

    }

    for(int j = n; j > 0; j--)

    {

        bestx[objs[E->level - 1].id] = E->lc;

        E = E->parent;

}

AddliveNode函数将一个新的活结点插入到优先队列中，该函数仅完成对新节点的初始化。

算法时间复杂度分析，分支限界法的时间复杂度取决于限界函数的时间复杂度，为O（n2^n）。

五、实验结果

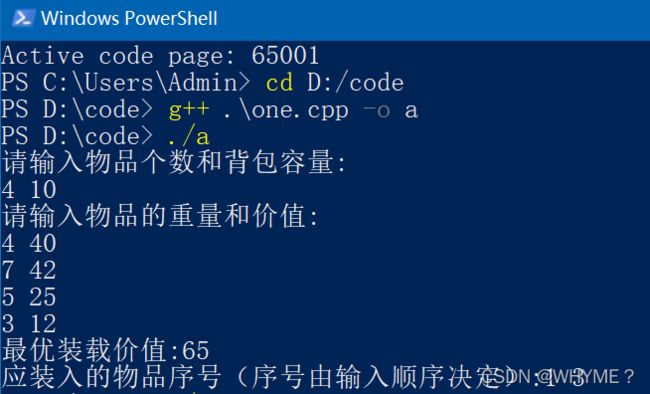
第一组输入，假设有4个物品，其重量分别为（4，7，5，3），价值分别为（40，42，25，12），背包容量为10，通过程序求解得最优价值为65，需装入得物品为物品1和物品3。

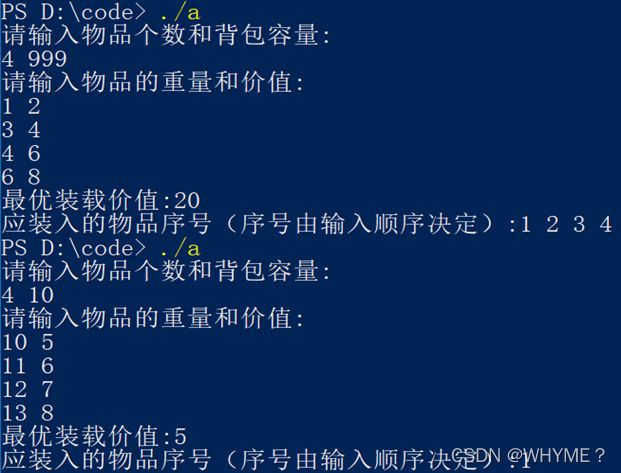
第二组和第三组输入都假设有4个物品，第二组输入物品的重量为（2，4，6，8），背包容量为999，通过程序求解得最优价值为20，可以装入全部物品。第三组输入物品重量为（10，11，12，13），背包容量为10，通过程序求解得最优价值为5，即装入第一个物品。

六、实验总结

对于0-1背包问题，已分别通过动态规划算法，回溯算法和分支定界方法进行了求解，时间复杂度为O（nc），O（n2^n），O（n2^n）。动态规划时通过寻找最优子结构，将整个问题的求解转换为子问题的求解，在转换的过程中判断某个具体的商品是否选择。

回溯法对于整个解空间的搜索，搜索时利用贪心性质（按照单位重量价值递减排序，估算可能的最高上界）、以及已经计算出的可行解作为界限进行剪枝，减少了很多计算量。

优先队列式分支限界法中，剪枝处理与回溯法相同，利用贪心性质（按照单位重量价值递减排序，估算可能的最高上界）、以及已经计算出的可行解作为界限进行剪枝。不同是，分支限界法使用优先队列，当针对一个结点进行扩展时，会将所有儿子结点进行展开，计算出所有儿子结点所能达到的最高上界。当一个优先队列中首结点是一个可行解则结束。

即回溯法与分支限界法的本质不同是搜索解空间的遍历方式不同。回溯法是深度优先搜索，穷尽解空间的所有可能（虽然也进行了剪枝）找到最优解。分支限界法是广度优先搜索，也是穷尽了解空间的所有可能以找到最优解。

通过对比学习三种算法求解0-1背包问题，加深了我对于动态规划，回溯算法和分支限界法的理解。对比学习完这些算法后，我认识到算法的精髓不在于其方式方法，而在于算法的思想思路，掌握了算法的思想，可以在潜移默化中解决很多问题。