计算方法 实验二

1实验目的和要求

实验目的：
(1)熟悉复化梯形方法、复化Simpson方法、梯形递推算法、龙贝格算法；
(2)能编程实现复化梯形方法、复化Simpson方法、梯形递推算法、龙贝格算法；
(3)理解并掌握自适应算法和收敛加速算法的基本思想；
(4)分析实验结果体会各种方法的精确度，建立计算机求解定积分问题的感性认识

程序任务：
（1）设计复化梯形公式求积算法，编制并调试相应的函数子程序
（2）设计复化辛卜生求积算法，编制并调试相应的函数子程序
（3）用龙贝格算法计算
输入：积分区间，误差限
输出：序列Tn，Sn，Cn，Rn及积分结果（参考书本P55的表2-5）

取n=2，4，8，16，精确解为0.9460831

2实验环境和工具

用matlab或C语言实现

3实验结果

3.1算法流程图

复化辛卜生公式算法流程：

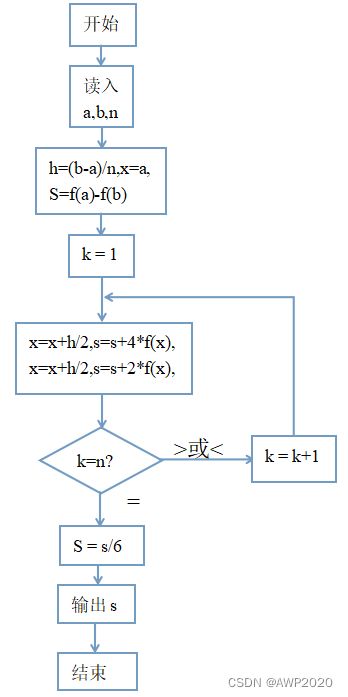
3.2程序核心代码

#include
#include
double ctl(double a,double b,int n);
double smp(double a,double b,int n);
void lbg(double a,double b,double e);
int main(void)
{
    int m,n;
    double a,b,s,e;
    printf("1.复化梯形公式\n2.复化辛卜生\n3.龙贝格算法\n\n");
    scanf("%d",&m);

    switch(m)
    {
    case 1:
        {
            printf("输入下限、上限、分段数。\n\n");
            scanf("%lf %lf %d",&a,&b,&n);
            s = ctl(a,b,n);
            printf("%lf\n",s);
            break;
        }
    case 2:
        {
            printf("输入下限、上限、分段数。\n\n");
            scanf("%lf %lf %d",&a,&b,&n);
            s = smp(a,b,n);
            printf("%lf\n",s);
            break;
        }
    case 3:
        {
            printf("输入下限、上限、误差限。\n\n");
            scanf("%lf %lf %lf",&a,&b,&e);
            lbg(a,b,e);
        }
    }
    return 0;
}

double f(double x)//原函数f(x)
{
    if(x==0)
    {
        return 1;
    }
    else
    {
        return sin(x)/x;
    }
}

double ctl(double a,double b,int n)//复化梯形公式
{
    double h = (b-a)/n;
    double t = 0;
    int i;

    for(i=1;i<n;i++)
    {
        t = t+f(a+i*h);
    }
    return h/2*(f(a)+2*t+f(b));
}

double smp(double a,double b,int n)//复化辛卜生
{
    double h = (b-a)/n;
    double x1 = f(a+h/2);
    double x2 = 0;
    int i;

    for(i=1;i<n;i++)
    {
        x1 = x1+f(a+i*h+h/2);
        x2 = x2+f(a+i*h);
    }
    return h/6*(f(a)+4*x1+2*x2+f(b));
}

void lbg(double a,double b,double e)//龙贝格算法
{
    double h = b-a;
    double t1,t2=0,s1=0,s2=0,c1=0,c2=0,r1=0,r2=1;
    double x,s;
    int k = 1;
    t1 = h/2*(f(a)+f(b));
    printf("\n%.7lf\n",t1);

    while(fabs(r2-r1)>=e)
    {
        s = 0;
        x = a+h/2;
        while(x<b)
        {
            s = s+f(x);
            x = x+h;
        }
        t2 = t1/2+h/2*s;
        s2 = t2+(t2-t1)/3;
        if(k==1)
        {
            k = k+1;
            h = h/2;
            t1 = t2;
            s1 = s2;
            printf("%.7lf\t%.7lf\n",t1,s1);
            continue;
        }
        c2 = s2+(s2-s1)/15;
        if(k==2)
        {
            k = k+1;
            h = h/2;
            t1 = t2;
            s1 = s2;
            c1 = c2;
            printf("%.7lf\t%.7lf\t%.7lf\n",t1,s1,c1);
            continue;
        }
        r2 = c2+(c2-c1)/63;
        k = k+1;
        h = h/2;
        t1 = t2;
        s1 = s2;
        c1 = c2;
        r1 = r2;
        printf("%.7lf\t%.7lf\t%.7lf\t%.7lf\n",t1,s1,c1,r1);
    }
}

3.3运行结果



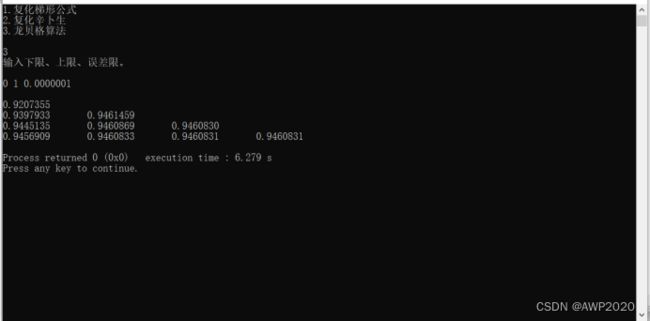
3.4运行结果分析
根据运行结果可以得出结论：
复化梯形公式、复化辛卜生公式、龙贝格算法的精确度是逐渐提高的，复化梯形公式的精确度较低，复化辛卜生公式的精度较前者有所提高，龙贝格算法的精度是三者之中最高的。

4实验心得

在本次实验之中，我又一次回顾了复化梯形公式、复化辛卜生公式和龙贝格算法。这三种算法不仅仅在数学上有很大的作用，在计算机编程方面也有极大的帮助。
我认为在计算机编程的过程中，算法是极为重要的一环，甚至可以说是最为重要的一环，没有好的算法，就难以构造好的函数，就难以得到符合要求的程序。而计算方法课程教会了我们很多好的算法，这些算法对于一个合格的程序员是必不可少的。将这三种算法牢记于心，对我们编程有莫大的好处。
这次实验开始的时候，我对于三种算法的印象已经有些模糊了，而这次实验让我重新回忆起了这三种算法，这也给我敲响了警钟，计算方法课程上的知识对于我们是必备的，我们应该经常回顾这些知识，温故而知新，只有在不断固化对过去知识的记忆，并去学习新的知识，才能在未来做到不后悔。
每一次实验，都是对过去知识的回顾，同样也是在应用过去的知识，我应该珍惜每一次的实验机会，利用好每一次实验，充分提高自己，巩固根基，才能在未来的学习生活中取得更好的成绩。