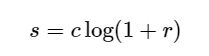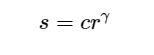引言
传统的图像增强方法主要分为两方面:空间域和频域。
空间域中增强方法:
- 直方图均衡化,对比度以及gama增强等(颜色的增强)
- 均值滤波,高斯滤波(模糊)
- 局部标准差实现对比度增强(锐化)
频域中增强方法如:
- 小波变换,在图像的某个变换域内,对图像的变换系数进行运算,然后通过逆变换获得图像增强效果。
一般来说,对于实际项目中,可能用其中一种或几种方法来进行图像增强效果一般会很差,我们更多的是对这些算法进行融合,来达到我们想要的效果。
1. 基于直方图均衡化的图像增强
直方图均衡化是通过调整图像的灰阶分布,使得在0~255灰阶上的分布更加均衡,提高了图像的对比度,达到改善图像主观视觉效果的目的。对比度较低的图像适合使用直方图均衡化方法来增强图像细节。
彩色图像的直方图均衡化实现:
Mat image = imread("D:/opencv练习图片/均衡化.png");
imshow("原图像", image);
Mat imageRGB[3];
split(image, imageRGB);
for (int i = 0; i < 3; i++)
{
equalizeHist(imageRGB[i], imageRGB[i]);
}
merge(imageRGB, 3, image);
imshow("直方图均衡化图像增强效果", image);
waitKey();
return 0;
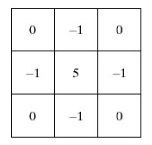
2. 基于拉普拉斯算子的图像增强
使用中心为5的8邻域拉普拉斯算子与图像卷积可以达到锐化增强图像的目的,拉普拉斯算子如下图所示:
拉普拉斯算子可以增强局部的图像对比度:
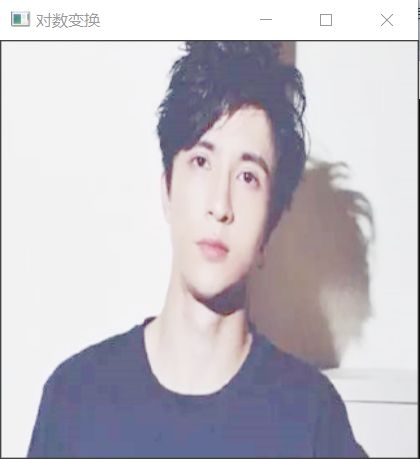
3. 基于对数Log变换的图像增强
对数变换可以将图像的低灰度值部分扩展,显示出低灰度部分更多的细节,将其高灰度值部分压缩,减少高灰度值部分的细节,从而达到强调图像低灰度部分的目的。变换方法:
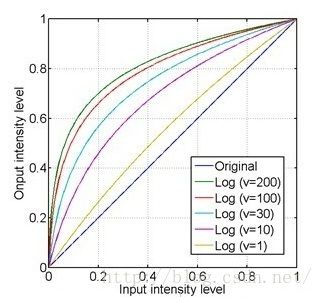
对数变换对图像低灰度部分细节增强的功能过可以从对数图上直观理解:
上0~0.4的低灰度部分经过对数运算后扩展到0~0.8的部分,而整个0.4~1的高灰度部分被投影到只有0.8~1的区间,这样就达到了扩展和增强低灰度部分,压缩高灰度部分的值的功能。
从上图还可以看到,对于不同的底数,底数越大,对低灰度部分的扩展就越强,对高灰度部分的压缩也就越强。
int main(int argc, char** argv)
{
Mat src;
src = imread("D:/opencv练习图片/对数变换.jpg");
imshow("Image", src);
Mat srcLog(src.size(), CV_32FC3);
for (int i = 0; i < src.rows; i++)
{
for (int j = 0; j < src.cols; j++)
{
//对数变换公式s = clog(1 + r)
srcLog.at(i, j)[0] = log(1 + src.at(i, j)[0]);
srcLog.at(i, j)[1] = log(1 + src.at(i, j)[1]);
srcLog.at(i, j)[2] = log(1 + src.at(i, j)[2]);
}
}
//归一化到0~255
normalize(srcLog, srcLog, 0, 255, NORM_MINMAX);
//转换成8bit图像显示
convertScaleAbs(srcLog, srcLog);
imshow("对数变换", srcLog);
waitKey(0);
return 0;
}
这使用的对数函数的底为10。由于灰度变换是灰度值之间的一对一的映射,而灰度值区间通常为[0,255],所以在进行灰度变换时,通常使用查表法。也就是,现将每个灰度值的映射后的结果计算出来,在变换时,通过查表得到变换后的灰度值。执行上面结果得到的结果如下:
由此可见对数变换对于整体对比度偏低并且灰度值偏低的图像增强效果较好。
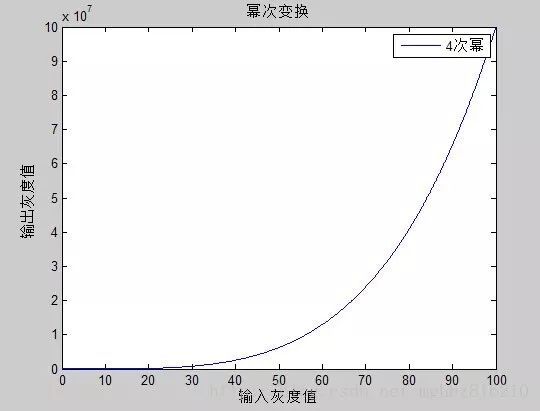
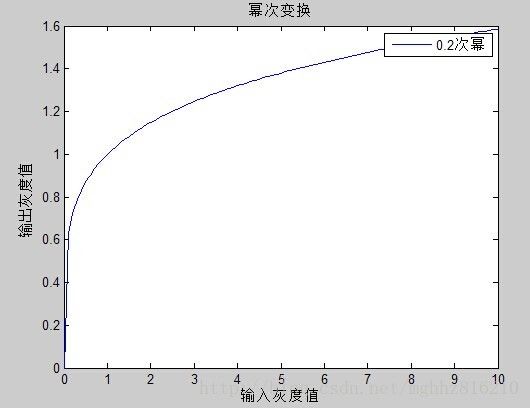
4. 基于伽马变换的图像增强
伽马变换主要用于图像的校正,对灰度值过高(图像过亮)或者过低(图像过暗)的图像进行修正,增加图像的对比度,从而改善图像的显示效果。
变换公式就是对原图像上每一个像素值做乘积运算:
伽马变换对图像的修正作用其实就是通过增强低灰度或高灰度的细节实现的,从伽马曲线可以直观理解:
伽马变换的效果与对数变换有点类似,对于γ<1,扩展低灰度范围,压缩高灰度范围;对于γ>1,压缩低灰度范围,扩展高灰度范围。这样就能够显示更多的图像的低灰度或者高灰度细节。
opencv实现:
原图是一张有点过曝的图像,高灰度部分的细节不清楚,通过伽马变换扩展高灰度部分,增强对比度:这里选择的参数为c = 1,r=4(r>1),来扩展图像的高灰度区域,其结果如下:
int main(int argc, char** argv)
{
float pixels[256];
for (int i = 0; i < 256; i++)
{
//i的四次方
pixels[i] = powf(i,4);
}
Mat src;
src = imread("D:/opencv练习图片/高曝光.png");
imshow("Image", src);
Mat srcLog(src.size(), CV_32FC3);
for (int i = 0; i < src.rows; i++)
{
for (int j = 0; j < src.cols; j++)
{
//幂律变换(伽马变换)
srcLog.at(i, j)[0] = pixels[src.at(i, j)[0]];
srcLog.at(i, j)[1] = pixels[src.at(i, j)[1]];
srcLog.at(i, j)[2] = pixels[src.at(i, j)[2]];
}
}
//归一化到0~255
normalize(srcLog, srcLog, 0, 255, NORM_MINMAX);
//转换成8bit图像显示
convertScaleAbs(srcLog, srcLog);
imshow("伽马变换", srcLog);
waitKey(0);
return 0;
}
还可以使用c = 1,r=0.4(r<1),来扩展图像的低灰度区域,其结果如下:
知识点:pow, powf, powl - 计算 x 的 y 次幂:xy
#include//头文件
double pow(double x, double y); float powf(float x, float y); long double powl(long double x, long double y);
总结
本文主要对图像的几种常见的灰度变换进行了总结。
- 图像反转,是图像线性变换的一种,可以得到图像负片,能够有效的增强图像的暗色区域中的白色或者灰色细节
- 对数变换,扩展图像中的低灰度区域,压缩图像中的高灰度区域,能够增强图像中的暗色区域的细节;反对数变换与此相反。对数变换还有个重要作用是,能够压缩图像灰度值的动态范围,在傅立叶变换中能够显示更多的变换后的频谱细节。
- 伽马变换,主要用于图像的校正,根据参数 γγ的选择不同,能够修正图像中灰度过高(γ>1)或灰度过低(γ<1)
参考链接:(8条消息) 图像灰度变换及实现_牧野的博客-CSDN博客_图像灰度变换
![]()