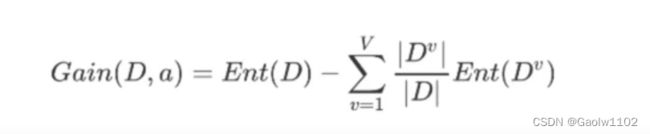熵、信息增益----决策树原理分析、代码实现与绘图

决策树的原理与实现

决策树是广泛用于分类和回归任务的模型，实际上它是由一层层的if/else问题中进行学习并得出结论的，本文章主要讲解据决策树的原理与实现。

两个重要的概念

决策树在构建过程中，选择根结点(中间结点)对于构造高准确度的决策树来说尤为重要，其中熵(shang)和信息增益两个属性决定了结点的选取。

熵

熵，又称香农熵，由著名科学家香农提出，它是衡量数据纯度的一种方法，其中熵值越小，表示数据越纯，反之亦然

为什么我们要引入熵这个概念呢？

别忘了我们的目标是分类任务(大多数)，即对一个数据进行分类，当然要求数据集的结果类别尽量纯洁、统一，有利于提升我们分类算法的准确度(这里需要注意的是，数据集初期的熵值不可能为 0 ，否则就不需要我们进行分类了，嘻嘻)

其中熵值的计算公式如下:

$$熵=-\sum _{i=1}^{n}P(i)\ast Log(P(i))$$

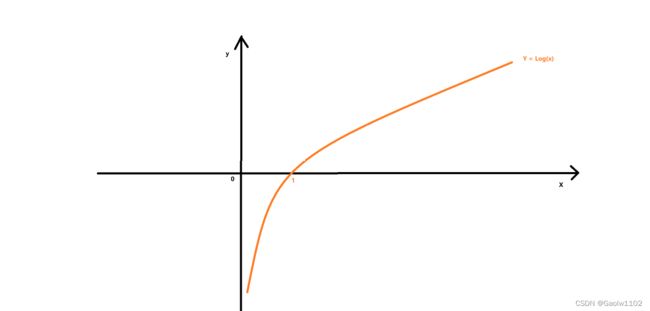
我们可以重点分析下Log(P(i))函数，以便于更好的理解:

其中P(i)表示每个类别结果占总数据集的比例，即概率始终P(i)<=1, 在上图即 X<=1

可见，当X=1时，则表示数据集中所有类别结果都相同，此时 熵 = 0， 表示纯度最高

相反，当每个P(i)值都很小时，即 X 很小，此时 -Log(X) 加起来就非常大，熵值就很大，表示纯度很低

例如，我们现在有两个初始结果集，如下

Y_1 = [1, 1, 1, 1, 1, 1, 1, 1]     #结果集中 结果类别都相同，均为 1，即概率为 1
Y_2 = [1, 2, 1, 2, 1, 2, 1, 2]     #结果集中包含两种结果，分别为 1, 2，各4个,  即每种概率为 0.5

可以计算它们的熵值:

熵(Y_1) = -(P(1)*Log(P(1))) = 0

熵(Y_2) = -(P(1)Log(P(1)) + P(2)Log(P(2))) = -(0.5(-1)+0.5(-1)) = 1

可见，熵(Y_1) < 熵(Y_2)，故集合Y_1的结果较纯

信息增益

信息增益的目标就是达成如下图一的分类效果，而排除图二的分类效果

我们知道，初始化数据集的熵值是固定的，一般来讲都较高，但是我们期望使用一个特征将数据集分为多个数据集(如上图)，即要求下层的数据集的平均熵值应尽可能的小，每个数据集的纯度尽可能高，那么

信息增益(Gain) = 父数据集熵值 - 子数据集的平均熵值

子数据集的平均熵值越低(如上图一)，信息增益就越高，越有益于分类，故我们需要寻找信息增益高的列作为特征切分数据集，依次排列高信息增益，由上至下构建决策树

我们来先计算下总的熵值, 熵 = - ((0.5)*Log(0.5) + (0.5)*Log(0.5)) = 1

接下来，我们来计算每种类别的信息增益

$$gai{n}_{0}1=1+[(\frac{18}{36}\ast P(1)\ast Log(P(1)))+(\frac{18}{36}\ast P(1)\ast Log(P(1)))]=1$$

$$gai{n}_{0}2=1+[[\frac{17}{36}\ast (P(\frac{3}{17})\ast Log(P(\frac{3}{17}))+P(\frac{14}{17})\ast Log(P(\frac{14}{17})))]+[\frac{19}{36}\ast (P(\frac{4}{19})\ast Log(P(\frac{4}{19}))+P(\frac{15}{19})\ast Log(P(\frac{15}{19})))]]=0.291$$

可见，特征一的信息增益更大，所以决策树构建过程中，首先会以特征一作为根节点进行构建，然后依次类推，构建决策树。

决策树的实现过程

以下将以代码的形式，构建并生成决策树。

创建数据集

import numpy as np
import pandas as pd

#创建数据集
def createDataset():
    
    #创建测试集
    dataset = {
        'AGE':[0, 0, 0, 0, 0, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2],
        'WORK':[0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0],
        'HOME':[0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0, 0, 0],
        'LOAN':[0, 1, 1, 0, 0, 0, 1, 1, 2, 2, 2, 1, 1, 2, 0],
        'TARGET':['no','no','yes','yes','no','no','no','yes','yes','yes','yes','yes','yes','yes','no']
    }
    
    #转化为 pandas 数组
    dataset = pd.DataFrame(dataset)
    
    return dataset
    

定义 熵 函数，输入数据集，返回熵值

#输入一个数据集，返回香农熵的值
def getEnt(dataset):
    
    n = dataset.shape[0]                             #获取数据集的行数，即数据量的大小
    
    iset = dataset.iloc[:,-1].value_counts()         #数据集的最后一列进行统计，统计各个元素的个数
    
    p = iset/n           #输出概率
    
    ent = (-p * np.log2(p)).sum()           #计算香农熵
    
    return ent                           #返回香农熵

计算信息增益、返回最大信息增益列下标

#做最优切分,重要重要重要
def bestSplit(dataset):
    base_ent = getEnt(dataset)             #获取本数据集的熵，作为基础熵
    best_gain = 0                          #定义最优信息增益，返回最优信息增益的列
    axis = -1                              #初始化列下标为 -1
    
    #循环所有特征列，寻找最优信息增益列
    for i in range(dataset.shape[1]-1):
        levels = dataset.iloc[:, i].value_counts().index        #获取第 i 列的不同特征类别, 准备计算每个类别的熵值
        ents = 0                                                #初始化熵值和为 0
        
        #循环特征内的每个类别
        for j in levels:
            
            #切分子数据集, !!!十分重要，要借鉴借鉴
            # dataset.iloc[:,i] == j 返回的结果为[False、False、False、...、True、True]类似的列表，就可以完成对数据集的切分
            child_set = dataset[dataset.iloc[:,i] == j]         
            
            ent = getEnt(child_set)                                   #获得该特征内一个类别的 熵 值
            
            #该特征的类别在数据集中的占比，即(child_set.shape[0]/dataset.shape[0])；再乘该特征 熵 值，累加
            ents += (child_set.shape[0]/dataset.shape[0])*ent
        
        #循环完毕后，得到按该特征切分所造成的下一轮n个子节点的 熵 值和
        
        info_gain = base_ent - ents              #总熵值和减去新熵值和，即为信息增益
        
        #使用打擂台的方式确定最大信息增益
        if (info_gain > best_gain):
            best_gain = info_gain
            axis = i                     #并保存其列所在的下标

    return axis            #返回该下标，用以切分数据集

分割数据集

#做分割
def mySplit(dataset, axis, value):
    
    #取出该特征的列的名称
    col = dataset.columns[axis]
    
    
    #取出数据集中[col]列中等于value值的所有数据行，并删除col列数据
    re_dataset = dataset.loc[dataset[col]==value, :].drop(col, axis=1)
    
    #返回新的数据集
    return re_dataset

组合板块，以递归方式构造决策树

#创建树
def createTree(dataset):
    feature_list = list(dataset.columns)                  #获取特征名称的集合(包括类别名称)
    
    class_list = dataset.iloc[:,-1].value_counts()        #获取dataset数据集的类型结果及它们的数量
    
    #如果此时数据集仅剩一种结果类型，则返回；或者仅剩下一列，即为类别结果列，也返回
    if class_list[0]==dataset.shape[0] or dataset.shape[1]==1:
        return class_list.index[0]
    
    axis = bestSplit(dataset)                            #获取最佳切分的列标(从0开始)

    best_feature = feature_list[axis]             #从特征名称列表中获取该最优信息增益对应的特征名称
       
    my_tree = {best_feature:{}}                   #创建初始决策数，以字典形式保存
    
    del feature_list[axis]                        #删除特征名称列表中该特征
    
    value_list = set(dataset.iloc[:, axis])       #set集合中，每个元素只能存在一次
    
    #遍历该特征内的所有类别标签,根据类别划分数据集
    for value in value_list:
        
        #递归地进行决策树地创建
        my_tree[best_feature][value] = createTree(mySplit(dataset, axis, value))
    
    #返回决策树，以字典的形式进行保存
    return my_tree
    

决策树的存储与读取

#决策树的存储
np.save('my_tree.npy', my_tree)

#决策树的读取
tree = np.load('my_tree.npy', allow_pickle=True).item()

测试决策树，并输出字典形式的决策树

dataset = createDataset()

my_tree = createTree(dataset)

my_tree

{'HOME': {0: {'WORK': {0: 'no', 1: 'yes'}}, 1: 'yes'}}

使用sklearn包构建决策树，画出决策树

from sklearn.tree import DecisionTreeClassifier          #导入sklearn包中的DecisionTreeClassifier类
from sklearn.tree import export_graphviz
import graphviz

dataset = createDataset()        #获取数据集
features = np.array(dataset.columns[:-1])

X = dataset.values[:,:-1]        #将DataFrame类型转化为 numpy类型，并进行切片操作，将数据集切分为 X, y
y = dataset.values[:,-1]

# [[0 0 0 0] [0 0 0 1] [0 1 0 1] [0 1 1 0] [0 0 0 0] [1 0 0 0] 
#   [1 0 0 1] [1 1 1 1] [1 0 1 2] [2 0 1 2] [2 0 1 2] [2 0 1 1] [2 1 0 1] [2 1 0 2] [2 0 0 0]]
# ['no' 'no' 'yes' 'yes' 'no' 'no' 'no' 'yes' 'yes' 'yes' 'yes' 'yes' 'yes' 'yes' 'no']

tree = DecisionTreeClassifier()
tree.fit(X, y)
res = tree.predict(np.array([[2, 1, 1, 2]]))

print(res)     #进行简单预测



#保存 决策树图形
export_graphviz(tree, out_file='tree.dot', class_names=['no', 'yes'], feature_names=features, impurity=False, filled=True)

#读取 决策树图形
with open('tree.dot') as fp:
    dot_graph = fp.read()

#输出数据集
print(dataset)
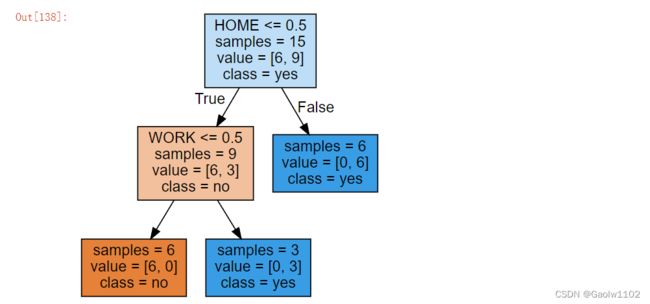
#输出 决策树图形
graphviz.Source(dot_graph)

['yes']
AGE  WORK  HOME  LOAN TARGET
0     0     0     0     0     no
1     0     0     0     1     no
2     0     1     0     1    yes
3     0     1     1     0    yes
4     0     0     0     0     no
5     1     0     0     0     no
6     1     0     0     1     no
7     1     1     1     1    yes
8     1     0     1     2    yes
9     2     0     1     2    yes
10    2     0     1     2    yes
11    2     0     1     1    yes
12    2     1     0     1    yes
13    2     1     0     2    yes
14    2     0     0     0     no