01背包问题

一、01背包问题

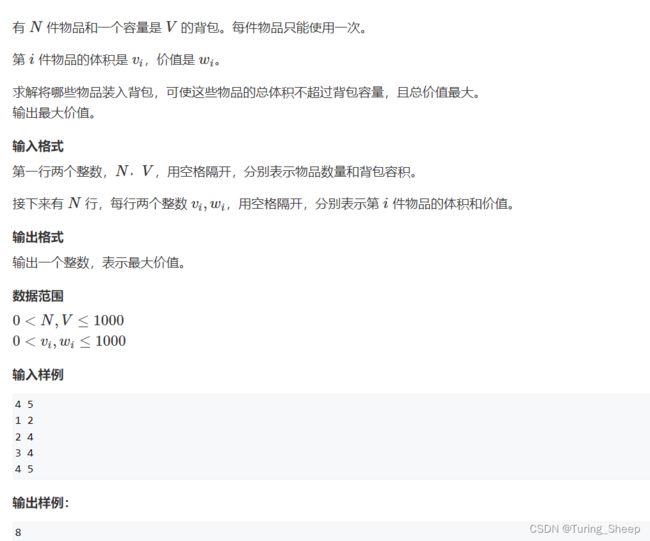
1、问题描述

2、问题性质分析

这道题给我们的第一感觉就是两个字：复杂。
为什么我们会觉得复杂呢？其实就是因为我们可做出的选法组合太多了，一下子根本不知道哪个选法是最优的。 说白了，我们感觉复杂的原因就在于问题的规模很大，需要做出的决策很多。复杂的决策问题会让我们无从下手，那么我们可以先从小规模的问题出发，寻找本质。

为了降低问题的复杂程度，我们可以选择缩小规模。缩小规模的方式就是将问题中涉及的变量变得很小。比如，在这道题目中，我们假设就一个物品1，体积是4，价值是5。你的容量是10。

那么此时，选择就很简单了对吧，你就两种选择，要么选物品1，要么不选物品1。很明显，我们选了这件物品就是最优解。

接着，我们稍微拓展一下规模：我们有两个物品：物品1，体积4，价值5，物品2，体积4，价值6。

那么我们此时就面临着两次选择：选不选第二个，选不选第一个。

假设我们选择了第二个物品。那么我们就又到了选择第一个物品的问题上，但此时我们是否选择第一个物品的场景就不同了。
我们此时的剩余容量是5，而上次面对物品1时，我们的容量是10。

那么当我们有三个物品的时候，我们做完物品2，物品3的选择后，是不是还会面对物品1的选择。此时，我们的剩余容量又不同了。

这个时候，我们会发现这个问题中的一些性质，比如：这道问题具有重叠子问题的性质。随着我们的选择，我们总是能遇到相应状态的子问题。

其次，我们不难发现，这道题还具备动态规划的另外两个性质：最优子结构与无后效性。为什么呢？

那我们刚才的问题为例，我们解决完物品2的最优选择后，还需要去解决物品1的最优选择问题。也就是说，我们想求当前问题的最优解，就需要去保证子问题的最优解，因此他具备最优子结构的性质。

接着，我们发现，我们只面对物品1时的最优解，并不受物品2的影响。所以它也具备无后效性的性质。

此时，我们就能够判断，这道题需要用动态规划的思路。

3、动态规划思路

那么动态规划求解的思路是什么呢？

动态规划就是需要我们提前记录好各个子问题的解，便于我们后续大规模问题的调用。而如何有条理的一步步算出规模不断扩大的子问题呢？

解决这个问题我们需要解决两个事情：

1、不同子问题之间的转换关系（状态方程的表示）

2、如何有顺序地扩大子问题规模（循环的书写）

（1）状态方程

a.状态表示：

假设我们的物品选择规模是i个，此时的背包容量是j，那么我们可以将当前的问题状态表示为：$f(i,j)$，那么$f(i,j)$的意思就是：当面前共有i个物品，背包容量为j时，我们所能携带的最大价值。

b.状态转移：

状态转移就是表示出当前问题和子问题之间的关系。

第$i$物品的价值记作$w[i]$,物品的体积记作$v[i]$。

状态转移方程的书写思路就是：活在当下。我们现在的目的不是一步解决这个问题，而是通过当前的决策将问题的规模减少。

我们遇到了第i个物品，所以我们当下的事情第i个物品选或者不选。两种情况下的最大值，就是我们的$f(i,j)$的解。

假设我们不选，那么我们此时的状态就只需要面对i-1个物品，背包容量也没变，即$f(i-1,j)$。
如果我们选了，那么我们此时的状态也是只需要面对i-1个物品，但此时的容量和价值发生了改变。此时需要注意的是，只有背包容量允许的条件下，我们才可能选。

通过上述思路，我们可以写出下面的转移方程：

$$f(i,j)=\{\begin{array}{ll}f(i-1,j)& j<v[i]\\ max(f(i-1,j),f(i-1,j-v[i])+w[i])& j\ge v[i]\end{array}$$

（2）循环的设计

循环设计是为了我们能够及时计算出后续问题需要的子问题结果，并有序地存储起来。我们刚才的举例中会发现，我们在后续问题中最后的子问题永远是第一个物品的选择问题，但面对第一个物品时的容量不同。因此，我们就可以先枚举出不同容量下面对第一个物品的最优解，然后再枚举面对第1，2个物品时，不同容量下的最优解，以此类推…

当然，循环的设计不唯一。
我们可以选择刚刚的设计方式，某个背包面对各个容量的最优解，也可以是某个容量，面对各个背包时的最优解。这两个区别就是内外循环颠倒了一下。二者都能有条不紊地枚举出子问题的结果。但是，前者可以进行空间优化，后者无法进行空间优化。为什么呢？我们后面再说。

3、代码模板

(1)朴素版

根据刚刚的思路，我们就能够写出朴素版的代码

#include
using namespace std;
const int N=1e3+10;
int f[N][N],v[N],w[N];
int n,m;
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        scanf("%d%d",v+i,w+i);
    }
    
    for(int i=1;i<=n;i++)//枚举背包规模
    {
        for(int j=0;j<=m;j++)//枚举容量
        {
        	//书写状态方程
            f[i][j]=f[i-1][j];
            if(j>=v[i])
            f[i][j]=max(f[i-1][j-v[i]]+w[i],f[i][j]);
        }
    }
    cout<<f[n][m]<<endl;
	return 0;
}

(2)优化版

朴素版的代码中，我们发现，我们当前问题的子问题都存储在了二维数组的上一行，因为写的都是i-1。所以，再往上的子问题记录就没有用了，只是多占空间而已。因此，我们不需要这么大的地方来存储所有子问题。

我们只需要一个一维数组。只需要来回覆盖即可。但是我们按照怎样的顺序来覆盖呢？

答案是我们逆序覆盖，为什么呢？这样做的目的是，保证每个物品只选择一次。为什么呢？

我们可以举个例子：

物品1 ：重量 1 价值 15
物品1 ：重量 2 价值 30
物品1 ：重量 4 价值 45

我们此时的dp数组为$f[j]$，这个里面的j表示的是当前的背包容量。假设我们正序遍历，
i=1的时候（意思是面对第一个物品），$f(1)=f(1-1)+15$,所以此时的$f(1)=15$那么此时的$f(1)$的意思是，我们选择了第一个物品后的最大价值。

此时，内层循环 j++，变成了j=2，所以$f(2)=f(2-1)+15=30$，此时的意思是：在$f(1)$的基础上再选择一次第一个物品后的最大价值，我们发现我们选择了两次第一个物品。

而我们如果逆序的话，则可以避免这个问题。大家可以自行举例。

二维数组之所以不需要是因为我们的数据都保存了下来，不会发生覆盖。我们从二维数组的写法中发现，我们用的都是上一行的正对的数据和上一行左侧的数据。所以我们此时不能先覆盖左侧的。从这个角度来看，我们也能够解释遍历顺序的问题。

所以，综合上面所讲的，我们就能够写下下面的代码。

#include
using namespace std;
const int N=1e3+10;
int f[N],v[N],w[N];
int n,m;
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        scanf("%d%d",v+i,w+i);
    }
    
    for(int i=1;i<=n;i++)//枚举背包规模
    {
        for(int j=m;j>=0;j--)//枚举容量
        {
        	//书写状态方程
            if(j>=v[i])
            f[j]=max(f[j-v[i]]+w[i],f[j]);
        }
    }
    cout<<f[n][m]<<endl;
	return 0;
}

如果我们的朴素版代码内外层循环颠倒，此时我们是无法使用空间优化的。为什么呢？

我们先来看颠倒后的朴素代码：

#include
using namespace std;
const int N=1010;
int v[N],w[N],f[N][N];
int n,m;
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        int a,b;
        scanf("%d%d",&a,&b);
        v[i]=a,w[i]=b;
    }
    for(int i=0;i<=m;i++)
    {
        for(int j=1;j<=n;j++)
        {
            f[i][j]=f[i][j-1];
            if(i>=v[j])
            f[i][j]=max(f[i][j],f[i-v[j]][j-1]+w[j]);
        }
    }
    cout<<f[m][n]<<endl;
    return 0;
}

由于用的不是上一行的数据，而是之前某一行的数据，所以我们不能利用覆盖的方式删除之前的数据。因为可能在后来的某一行会用到最开始的第一行数据，跨度很大。我们必须全部保存下来。