从互信息角度理解生成对抗网络:infoGAN
文章目录
- 回顾:生成对抗网络 Generative Adversarial Nets
-
- 从互信息角度理解GAN
- InfoGAN: 一种用了2次变分来近似推断的方法
- GAN 其实在错误的方向上优化
- 参考资料
回顾:生成对抗网络 Generative Adversarial Nets
GAN的目标就是要学到一个数据分布为p(x)的生成网络G,即希望 p G ( x ) \displaystyle p_{G}( x) pG(x)与 P d a t a ( x ) \displaystyle P_{data}( x) Pdata(x)尽可能接近。为此这里引入了一个判别网络D,这个判别网络的作用就是用来尽可能区分 x ∼ P G ( x ) \displaystyle x\sim P_{G}( x) x∼PG(x)与 x ∼ P d a t a ( x ) \displaystyle x\sim P_{data}( x) x∼Pdata(x)的数据。这一个minmax的游戏可以用下面的公式表达:
min G max D V ( D , G ) = E p ( x ) [ log ( D ( x ) ) ] + E p ( z ) [ log ( 1 − D ( G ( z ) ) ) ] \min_{G}\max_{D} V(D,G)=E_{p(\mathbf{x} )} [\log (D(\mathbf{x} ))]+E_{p(\mathbf{z} )} [\log (1-D(G(\mathbf{z} )))] GminDmaxV(D,G)=Ep(x)[log(D(x))]+Ep(z)[log(1−D(G(z)))]
当我们固定G时,判别器所使用的目标函数是:
max D V ( D , G ) = E p ( x ) [ log ( D ( x ) ) ] + E x G ∼ p G ( x ) [ log ( 1 − D ( x G ) ) ] \max_{D} V(D,G)=E_{p(\mathbf{x} )} [\log (D(\mathbf{x} ))]+E_{x_{G} \sim p_{G}( x)} [\log (1-D(x_{G} ))] DmaxV(D,G)=Ep(x)[log(D(x))]+ExG∼pG(x)[log(1−D(xG))]
这里把 G ( z ) \displaystyle G(\mathbf{z} ) G(z)所产生的样本,用 x G \displaystyle x_{G} xG来代替了。在这里,如何判别器D判断样本为真实的话,那么就等于1,如果是假的话,就等于0,可以想象,当判别器最优时,左边那项一定等于0,因为来自真实样本,右边那项也等于0,因为样本是来自 x G \displaystyle x_{G} xG的。这时候这个目标函数就是最大的(这个目标函数一定小于等于0,因为概率是小于等于1的,那么概率的对数就是小于等于0的)。
可以证明,当D达到最优时,即 D ∗ ( x ) = p d a t a ( x ) p d a t a ( x ) + p G ( x ) D^{*} (\mathbf{x} )=\frac{p_{data} (\mathbf{x} )}{p_{data} (\mathbf{x} )+p_{G} (\mathbf{x} )} D∗(x)=pdata(x)+pG(x)pdata(x) ,该目标函数等价于优化JS散度:
V ( D G ∗ , G ) = ∫ p d a t a ( x ) log p d a t a ( x ) p d a t a ( x ) + p G ( x ) d x + ∫ p G ( x ) log p G ( x ) p d a t a ( x ) + p G ( x ) d x − log 4 + log 4 = ∫ p d a t a ( x ) log p d a t a ( x ) p d a t a ( x ) + p G ( x ) d x + ∫ p G ( x ) log p G ( x ) p d a t a ( x ) + p G ( x ) d x − log 4 + log 4 ∫ p G ( x ) d x = ∫ p d a t a ( x ) log p d a t a ( x ) p d a t a ( x ) + p G ( x ) d x + ∫ p G ( x ) log p G ( x ) p d a t a ( x ) + p G ( x ) d x − log 4 + log 2 ∫ p d a t a ( x ) d x + log 2 ∫ p G ( x ) d x = ∫ p d a t a ( x ) log 2 p d a t a ( x ) p d a t a ( x ) + p G ( x ) d x + ∫ p G ( x ) log 2 p G ( x ) p d a t a ( x ) + p G ( x ) d x − log 4 = ∫ p d a t a ( x ) log p d a t a ( x ) p d a t a ( x ) + p G ( x ) 2 d x + ∫ p G ( x ) log p G ( x ) p d a t a ( x ) + p G ( x ) 2 d x − log 4 = D K L ( p d a t a ( x ) ∣ ∣ p d a t a ( x ) + p G ( x ) 2 ) + D K L ( p ( x ) ∣ ∣ p d a t a ( x ) + p G ( x ) 2 ) − log 4 = 2 ⋅ J S D ( p d a t a ( x ) ∣ ∣ p G ( x ) ) − log 4 \begin{aligned} V(D^{*}_{G} ,G) & =\int p_{data} (\mathbf{x} )\log\frac{p_{data} (\mathbf{x} )}{p_{data} (\mathbf{x} )+p_{G} (\mathbf{x} )} d\mathbf{x} +\int p_{G} (\mathbf{x} )\log\frac{p_{G} (\mathbf{x} )}{p_{data} (\mathbf{x} )+p_{G} (\mathbf{x} )} d\mathbf{x} -\log 4\\ & +\log 4\\ & =\int p_{data} (\mathbf{x} )\log\frac{p_{data} (\mathbf{x} )}{p_{data} (\mathbf{x} )+p_{G} (\mathbf{x} )} d\mathbf{x} +\int p_{G} (\mathbf{x} )\log\frac{p_{G} (\mathbf{x} )}{p_{data} (\mathbf{x} )+p_{G} (\mathbf{x} )} d\mathbf{x} -\log 4\\ & +\log 4\int p_{G} (\mathbf{x} )d\mathbf{x}\\ & =\int p_{data} (\mathbf{x} )\log\frac{p_{data} (\mathbf{x} )}{p_{data} (\mathbf{x} )+p_{G} (\mathbf{x} )} d\mathbf{x} +\int p_{G} (\mathbf{x} )\log\frac{p_{G} (\mathbf{x} )}{p_{data} (\mathbf{x} )+p_{G} (\mathbf{x} )} d\mathbf{x} -\log 4\\ & +\log 2\int p_{data} (\mathbf{x} )d\mathbf{x} +\log 2\int p_{G} (\mathbf{x} )d\mathbf{x}\\ & =\int p_{data} (\mathbf{x} )\log\frac{2p_{data} (\mathbf{x} )}{p_{data} (\mathbf{x} )+p_{G} (\mathbf{x} )} d\mathbf{x} +\int p_{G} (\mathbf{x} )\log\frac{2p_{G} (\mathbf{x} )}{p_{data} (\mathbf{x} )+p_{G} (\mathbf{x} )} d\mathbf{x} -\log 4\\ & =\int p_{data} (\mathbf{x} )\log\frac{p_{data} (\mathbf{x} )}{\frac{p_{data} (\mathbf{x} )+p_{G} (\mathbf{x} )}{2}} d\mathbf{x} +\int p_{G} (\mathbf{x} )\log\frac{p_{G} (\mathbf{x} )}{\frac{p_{data} (\mathbf{x} )+p_{G} (\mathbf{x} )}{2}} d\mathbf{x} -\log 4\\ & =D_{KL}\left( p_{data} (\mathbf{x} )||\frac{p_{data} (\mathbf{x} )+p_{G} (\mathbf{x} )}{2}\right) +D_{KL}\left( p(\mathbf{x} )||\frac{p_{data} (\mathbf{x} )+p_{G} (\mathbf{x} )}{2}\right) -\log 4\\ & =2\cdot JSD(p_{data} (\mathbf{x} )||p_{G} (\mathbf{x} ))-\log 4 \end{aligned} V(DG∗,G)=∫pdata(x)logpdata(x)+pG(x)pdata(x)dx+∫pG(x)logpdata(x)+pG(x)pG(x)dx−log4+log4=∫pdata(x)logpdata(x)+pG(x)pdata(x)dx+∫pG(x)logpdata(x)+pG(x)pG(x)dx−log4+log4∫pG(x)dx=∫pdata(x)logpdata(x)+pG(x)pdata(x)dx+∫pG(x)logpdata(x)+pG(x)pG(x)dx−log4+log2∫pdata(x)dx+log2∫pG(x)dx=∫pdata(x)logpdata(x)+pG(x)2pdata(x)dx+∫pG(x)logpdata(x)+pG(x)2pG(x)dx−log4=∫pdata(x)log2pdata(x)+pG(x)pdata(x)dx+∫pG(x)log2pdata(x)+pG(x)pG(x)dx−log4=DKL(pdata(x)∣∣2pdata(x)+pG(x))+DKL(p(x)∣∣2pdata(x)+pG(x))−log4=2⋅JSD(pdata(x)∣∣pG(x))−log4
从互信息角度理解GAN
现在假设有一个隐变量s,当s=0时,数据服从真实的分布 p d a t a \displaystyle p_{data} pdata,当s=1时,数据则不服从真实的分布 p f a k e \displaystyle p_{fake} pfake。
s ∼ p ^ s ( s ) , x ∼ p ^ ( x ∣ s ) p ^ ( x ∣ s = 0 ) = p d a t a ( x ) , p ^ ( x ∣ s = 1 ) = p f a k e ( x ) s\sim \hat{p}_{s}( s) ,x\sim \hat{p}( x|s)\\ \hat{p}( x|s=0) =p_{data}( x) ,\hat{p}( x|s=1) =p_{fake}( x) s∼p^s(s),x∼p^(x∣s)p^(x∣s=0)=pdata(x),p^(x∣s=1)=pfake(x)
我们一般希望生成模型能够学习到数据的真实分布 p d a t a ( x ) \displaystyle p_{data}( x) pdata(x),那么我们可以通过最小化以下互信息来实现:
I ( s , x ) = K L ( p ^ ( x , s ) ∥ p ^ ( x ) p ^ ( s ) ) I( s,x) =KL\left(\hat{p}( x,s) \| \hat{p}( x)\hat{p}( s)\right) I(s,x)=KL(p^(x,s)∥p^(x)p^(s))
显然当互信息等于0时,一定有 p f a k e ( x ) = p d a t a ( x ) \displaystyle p_{fake}( x) =p_{data}( x) pfake(x)=pdata(x),然而这个互信息是很难计算的,那么我们可以使用变分的方法,对互信息引入变分分布q,得到互信息的下界:
L [ p ; q ] = I ( s ; x ) − E p ~ ( x ) [ K L [ p ~ ( s ∣ x ) ∣ ∣ q ( s ∣ x ) ] ] = H ( s ) − H ( s ∣ x ) − E p ~ ( s , x ) [ p ~ ( s ∣ x ) ∣ ∣ q ( s ∣ x ) ] = H [ s ] + E p ~ ( s ) E p ~ ( x ∣ s ) [ log q ( s ∣ x ) ] \begin{aligned} \mathcal{L} [p;q] & =\mathrm{I}( s;x) -E_{\tilde{p} (x)} [\mathrm{KL} [\tilde{p} (s|x)||q(s|x)]]\\ & =H( s) -H( s|x) -E_{\tilde{p} (s,x)} [\tilde{p} (s|x)||q(s|x)]\\ & =\mathrm{H} [s]+E_{\tilde{p}( s)} E_{\tilde{p} (x|s)} [\log q(s|x)] \end{aligned} L[p;q]=I(s;x)−Ep~(x)[KL[p~(s∣x)∣∣q(s∣x)]]=H(s)−H(s∣x)−Ep~(s,x)[p~(s∣x)∣∣q(s∣x)]=H[s]+Ep~(s)Ep~(x∣s)[logq(s∣x)]
在这里q(s|x)的作用就是用来近似p(s|x).更有趣的是,其实我们可以把q看作是GAN的判别器!我们把上面的下界展开写成:
H [ s ] + p ~ ( s = 0 ) E x d a t a ∼ p ~ ( x ∣ s = 0 ) [ log ( 1 − q ( s = 1 ∣ x d a t a ) ) ] + p ~ ( s = 1 ) E x f a k e ∼ p ~ ( x ∣ s = 1 ) [ log q ( s = 1 ∣ x f a k e ) ] . \mathrm{H} [s]+\tilde{p} (s=0)\mathbb{E}_{x_{data} \sim \tilde{p} (x|s=0)} [\log (1-q(s=1|x_{data} ))]+\tilde{p} (s=1)\mathbb{E}_{x_{fake} \sim \tilde{p} (x|s=1)} [\log q(s=1|x_{fake} )]. H[s]+p~(s=0)Exdata∼p~(x∣s=0)[log(1−q(s=1∣xdata))]+p~(s=1)Exfake∼p~(x∣s=1)[logq(s=1∣xfake)].
有没有觉得很熟悉?我们发现右边那一项恰好对应着由生成器产生的fake样本,而q恰好是用来判断样本是真的还是假的。也就是说,当G固定时,判别器实际上就是在最大化I(s,x)互信息的下界。(注意这个互信息里的x并不是真实分布的x,而是一个真实与虚假混合在一起的x)。所以GAN的判别器实际上是一个变分函数,用来近似某个混合分布x的后验的。
实际上,GAN的目标函数与互信息的联系本质上是JS散度与互信息的联系。JS散度 J S ( P ∥ Q ) \displaystyle JS( P\| Q) JS(P∥Q),可以看做是一个指示变量Z与X的互信息,当Z=0时,X的分布服从P,Z=1时,X的分布服从Q,当不给定Z时,X是一个混合分布,它服从M=(P+Q)/2,可以证明 J S ( P ∥ Q ) = I ( X ; Z ) \displaystyle JS( P\| Q) =I( X;Z) JS(P∥Q)=I(X;Z):
I ( X ; Z ) = H ( X ) − H ( X ∣ Z ) = − ∑ M log M + 1 2 [ ∑ P log P + ∑ Q log Q ] = − ∑ P 2 log M − ∑ Q 2 log M + 1 2 [ ∑ P log P + ∑ Q log Q ] = 1 2 ∑ P ( log P − log M ) + 1 2 ∑ Q ( log Q − log M ) = J S D ( P ∥ Q ) \begin{aligned} I(X;Z) & =H(X)-H(X|Z)\\ & =-\sum M\log M+\frac{1}{2}\left[\sum P\log P+\sum Q\log Q\right]\\ & =-\sum \frac{P}{2}\log M-\sum \frac{Q}{2}\log M+\frac{1}{2}\left[\sum P\log P+\sum Q\log Q\right]\\ & =\frac{1}{2}\sum P(\log P-\log M) +\frac{1}{2}\sum Q(\log Q-\log M)\\ & =\mathrm{JSD} (P\parallel Q) \end{aligned} I(X;Z)=H(X)−H(X∣Z)=−∑MlogM+21[∑PlogP+∑QlogQ]=−∑2PlogM−∑2QlogM+21[∑PlogP+∑QlogQ]=21∑P(logP−logM)+21∑Q(logQ−logM)=JSD(P∥Q)
详情可以看:Wiki: Jensen–Shannon divergence
InfoGAN: 一种用了2次变分来近似推断的方法
然后很多时候,只要你的生成器 P G \displaystyle P_{G} PG足够好,那么GAN从一个随机噪声z生成出来的p(x|z)与这个随机噪声z是没什么关系的,即 p G ( x ∣ z ) = p G ( x ) \displaystyle p_{G}( x|z) =p_{G}( x) pG(x∣z)=pG(x),虽然,这种情况,如果我们仅仅是需要是一个好的生成器的话,那么其实并没有什么大问题。但是,我们常常想要的是模型具有一定的可解释性,比如,手写数据集MNIST,我们希望模型能用10个离散的z来表达不同的数据,然后再用几个连续的噪声来表达字体的粗细。更进一步说,我们认为如果z能够包含这些语意相关的特征,他的泛化能力应该会更强,模型会更加的精确。
为了解决这个问题,infoGAN将输入的噪声分成2部分
-
z:这是无可压缩的部分,我们认为这部分不存在任意语意信息,但却是不可或缺的;
-
c:这部分则关联着我们关心的语意或可解释的特征,因此我们要求c与产生出来的图像要尽可能相关。
min G max D V I ( D , G ) = V ( D , G ) − λ I ( c ; G ( z , c ) ) \min_{G}\max_{D} V_{I} (D,G)=V(D,G)-\lambda I( c;G( z,c)) GminDmaxVI(D,G)=V(D,G)−λI(c;G(z,c))
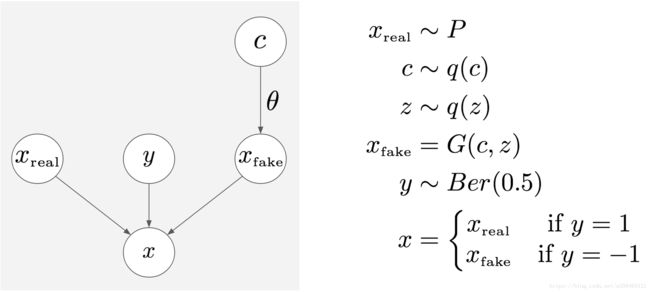
上面我们建立了JS散度与互信息的关系,其关系表明GAN就是一个混合模型X与一个指示变量的互信息。我们现在从这个混合模型出发,用一个概率图模型来理解 infoGAN [3]. 图中的参数表示:
-
c是一个隐变量,从先验分布 p ( c ) p(c) p(c)中抽取
-
x f a k e \displaystyle x_{fake} xfake是一个由生成器,其参数为 θ \theta θ,结合c产生的样本
-
y 是一个指示变量,用来区分样本到底是真实的还是假的
-
x是判别器最终收到样本x,这个样本来自哪里取决于y的取值,如果y=0就是来自真实分布,y=1就来自假的分布。
于是我们可以导出infoGAN的目标函数:
ℓ i n f o G A N ( θ ) = I [ x , y ] − λ I [ x f a k e , c ] \ell _{infoGAN} (\theta )=I[x,y]-\lambda I[x_{fake} ,c] ℓinfoGAN(θ)=I[x,y]−λI[xfake,c]
不要忘了普通GAN的目标函数是:
ℓ G A N ( θ ) = I [ x , y ] \ell _{GAN} (\theta )=I[x,y] ℓGAN(θ)=I[x,y]
第一项的互信息实际上就等价于JS散度,第二项则是由infoGAN引入的项。然而infoGAN引入的这一项互信息,因为我们不知道后验分布 p ( c ∣ x ) \displaystyle p( c|x) p(c∣x)的形式,所以很难求解,为了优化这个互信息,引入了一个 q ( c ∣ x ) \displaystyle q( c|x) q(c∣x)去近似这个p,从而导出了互信息的下界:
I ( c ; G ( z , c ) ) = H ( c ) − H ( c ∣ G ( z , c ) ) = E x ∼ p G ( x ∣ z , c ) E c ∼ p ( c ∣ x ) log p ( c ∣ x ) + H ( c ) = E x ∼ p G ( x ∣ z , c ) [ E c ∼ p ( c ∣ x ) log p ( c ∣ x ) q ( c ∣ x ) + E c ∼ p ( c ∣ x ) log q ( c ∣ x ) ] + H ( c ) = E x ∼ p G ( x ∣ z , c ) [ K L ( p ( c ∣ x ) ∥ q ( c ∣ x ) ) ⏟ ⩾ 0 + E c ∼ p ( c ∣ x ) log q ( c ∣ x ) ] + H ( c ) ⩾ E x ∼ p G ( x ∣ z , c ) E c ∼ p ( c ∣ x ) log q ( c ∣ x ) + H ( c ) \begin{aligned} I( c;G( z,c)) & =H( c) -H( c|G( z,c))\\ & =E_{x\sim p_{G}( x|z,c)} E_{c\sim p( c|x)}\log p( c|x) +H( c)\\ & =E_{x\sim p_{G}( x|z,c)}\left[ E_{c\sim p( c|x)}\log\frac{p( c|x)}{q( c|x)} +E_{c\sim p( c|x)} \log q( c|x)\right] +H( c)\\ & =E_{x\sim p_{G}( x|z,c)}\left[\underbrace{KL( p( c|x) \| q( c|x))}_{\geqslant 0} +E_{c\sim p( c|x)} \log q( c|x)\right] +H( c)\\ & \geqslant E_{x\sim p_{G}( x|z,c)} E_{c\sim p( c|x)}\log q( c|x) +H( c) \end{aligned} I(c;G(z,c))=H(c)−H(c∣G(z,c))=Ex∼pG(x∣z,c)Ec∼p(c∣x)logp(c∣x)+H(c)=Ex∼pG(x∣z,c)[Ec∼p(c∣x)logq(c∣x)p(c∣x)+Ec∼p(c∣x)logq(c∣x)]+H(c)=Ex∼pG(x∣z,c)⎣⎡⩾0 KL(p(c∣x)∥q(c∣x))+Ec∼p(c∣x)logq(c∣x)⎦⎤+H(c)⩾Ex∼pG(x∣z,c)Ec∼p(c∣x)logq(c∣x)+H(c)
这个下界有个问题,那就是期望里面的 p ( c ∣ x ) \displaystyle p( c|x) p(c∣x)仍然是没法计算的,这里用到一个技巧,让我们不再需要从 p ( c ∣ x ) p(c|x) p(c∣x)中抽样:
L I ( G , D ) = E c ∼ p ( c ) , x ∼ G ( x , c ) [ log Q ( c ∣ x ) ] + H ( c ) = E x ∼ p G ( x ∣ z , c ) E c ∼ p ( c ∣ x ) log Q ( c ∣ x ) + H ( c ) ⩽ I ( c ; G ( z , c ) ) \begin{aligned} L_{I}( G,D) & =E_{c\sim p( c) ,x\sim G( x,c)}[\log Q( c|x)] +H( c)\\ & =E_{x\sim p_{G}( x|z,c)} E_{c\sim p( c|x)} \log Q( c|x) +H( c)\\ & \leqslant \ I( c;G( z,c)) \end{aligned} LI(G,D)=Ec∼p(c),x∼G(x,c)[logQ(c∣x)]+H(c)=Ex∼pG(x∣z,c)Ec∼p(c∣x)logQ(c∣x)+H(c)⩽ I(c;G(z,c))
于是,我们在求解G的时候,就可以用这个下界来代替互信息,再加上V(D,G)作为目标函数
min G , Q max D V I ( D , G ) = V ( D , G ) − λ L I ( G , D ) \min_{G,Q}\max_{D} V_{I} (D,G)=V(D,G)-\lambda L_{I}( G,D) G,QminDmaxVI(D,G)=V(D,G)−λLI(G,D)
值得一提的是,对于任意的互信息 I ( X , Y ) \displaystyle I( X,Y) I(X,Y),其实都有一个下界,其核心思想就是用q(y|x)去近似p(y|x),它的推导更上面的是类似:
I [ X , Y ] = H [ Y ] − E x H [ Y ∣ X = x ] = H [ Y ] + E x E y ∣ x log p ( y ∣ x ) = H [ Y ] + E x E y ∣ x log p ( y ∣ x ) q ( y ∣ x ) q ( y ∣ x ) = H [ Y ] + E x E y ∣ x log q ( y ∣ x ) + E x E y ∣ x log p ( y ∣ x ) q ( y ∣ x ) = H [ Y ] + E x E y ∣ x log q ( y ∣ x ) + E x K L [ p ( y ∣ x ) ∥ q ( y ∣ x ) ] ≥ H [ Y ] + E x E y ∣ x log q ( y ∣ x ) \begin{aligned} I[X,Y] & =H[Y]-\mathbb{E}_{x} H[Y|X=x]\\ & =H[Y]+\mathbb{E}_{x}\mathbb{E}_{y|x}\log p(y|x)\\ & =H[Y]+\mathbb{E}_{x}\mathbb{E}_{y|x}\log\frac{p(y|x)q(y|x)}{q(y|x)}\\ & =H[Y]+\mathbb{E}_{x}\mathbb{E}_{y|x}\log q(y|x)+\mathbb{E}_{x}\mathbb{E}_{y|x}\log\frac{p(y|x)}{q(y|x)}\\ & =H[Y]+\mathbb{E}_{x}\mathbb{E}_{y|x}\log q(y|x)+\mathbb{E}_{x} KL[p(y|x)\|q (y|x)]\\ & \geq H[Y]+\mathbb{E}_{x}\mathbb{E}_{y|x}\log q(y|x) \end{aligned} I[X,Y]=H[Y]−ExH[Y∣X=x]=H[Y]+ExEy∣xlogp(y∣x)=H[Y]+ExEy∣xlogq(y∣x)p(y∣x)q(y∣x)=H[Y]+ExEy∣xlogq(y∣x)+ExEy∣xlogq(y∣x)p(y∣x)=H[Y]+ExEy∣xlogq(y∣x)+ExKL[p(y∣x)∥q(y∣x)]≥H[Y]+ExEy∣xlogq(y∣x)
GAN 其实在错误的方向上优化
从上面的内容可以知道GAN的目标函数可以看做是互信息的变分下界。它的优化分为两步:
min G max D V ( D , G ) \min_{G}\max_{D} V(D,G) GminDmaxV(D,G)
第一步是固定G,然后最大化D对应的下界。另一步是固定D,然后最小化G对应的下界,这时候或许就会出现问题,因为他往错误的优化方向优化了,本来下界应该是要最大化的,而这里反而却最小化了,这或许部分解释了GAN不稳定的原因。
参考资料
[1] Chen, Xi, et al. “Infogan: Interpretable representation learning by information maximizing generative adversarial nets.” Advances in neural information processing systems. 2016.
[2] http://www.yingzhenli.net/home/blog/?p=421
[3] https://www.inference.vc/infogan-variational-bound-on-mutual-information-twice/