【编程算法】跳跃游戏ⅠⅡⅢ(Python解法)
写这篇文章源于之前4.10做的字节跳动的笔试,第二道编程题就是跳跃游戏类,可以说和牛客或者力扣上边的解题做法是完全一样的,可惜当时我才刚开始学习算法。深入了解该类型后发现真的很有意思,这篇文章给大家分享一下本人的思路及解题方法,算是系统性地阐述了该类问题的解法,假如把这几题搞懂,我觉得在遇到该类问题便能做到得心应手了。
目录
一、贪心算法
二、跳跃游戏Ⅰ
题目描述:
解题思路:
解法1:
解法2:
三、拓展问题
1、固定跳跃游戏:
2、跳跃游戏Ⅱ(最少步数/次数):
3、跳跃游戏Ⅲ(最佳路径)
总结
一、贪心算法
贪心算法,是寻找最优解问题的常用方法,这种方法模式一般将求解过程分成若干个步骤,但每个步骤都应用贪心原则,选取当前状态下最好/最优的选择(局部最有利的选择),并以此希望最后堆叠出的结果也是最好/最优的解。
对于跳跃问题来说,贪心算法是不错的选择,跳跃问题需要你每次做出选择,并选择能带来更多收益的位置,可通过for/while遍历+条件语句来解决,常规具体步骤:
步骤1:从某个初始解出发;
步骤2:采用迭代的过程,当可以向目标前进一步时,就根据局部最优策略,得到一部分解,缩小问题规模;
步骤3:将所有解综合起来。
二、跳跃游戏Ⅰ
题目描述:
字节跳动题目:给定一个非负整数数组nums,例如:[2,0,1,0,3],位置上的数值代表了能量值的多少,给定机器人初始位于第一个位置,机器人走一步,需要消耗1个单位能量,如果当前位置能量为0,则无法走了。arr每个位置就是能量值arri,机器人可以选择走0–arri步,请问你机器人能走到终点N位置吗?
示例:
输入: [2,3,1,1,4]
输出: true
解释: 我们可以先跳 1 步,从位置 0 到达 位置 1, 然后再从位置 1 跳 3 步到达最后一个位置。
输入: [3,2,1,0,4]
输出: false
解释: 无论怎样,你总会到达索引为 3 的位置。但该位置的最大跳跃长度是 0 , 所以你永远不可能到达最后一个位置。
其实字节的题目只是跳跃游戏的变形,不信你看跳跃游戏的原题(来自牛客)
解题思路:
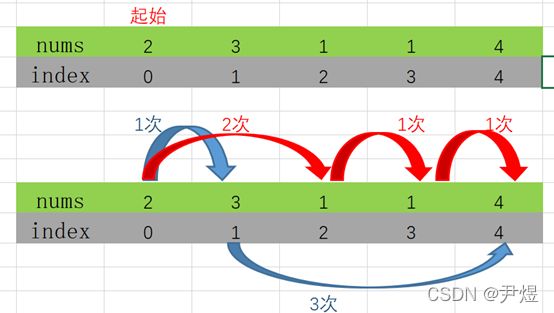
其实做算法题重要的理解他的逻辑,看下图,初始位置是index=0,nums=2,那么可以选择跳一次或者两次,假如选择跳一次,那么跳到index=2,由于nums=1,再跳一次...最后到达队尾;假如选择跳二次,先跳到index=1,再选择跳三次就可直接到达队尾。(跳跃后,不论选择跳几次,下一次的跳跃以index上的nums为准)
解法1:
1.这题存在一个核心参数,那就是max_pos,它是指当前能跳到最远的位置,max_pos = index + nums[index],坐标和数值的和决定了它能跳多远。参考上图,index=0时,他的max_pos=2,最远能跳到index=2,index=2时,它的max_pos=3,最远能跳到index=3,只有掌握了这个参数才能明白此解法。
for index in range(n):
if index <= max_pos and index + nums[index] > max_pos:
max_pos = index + nums[index]
2.还有一个关键的循环和条件语句,因为数组本身是不存在坐标的,因此通过len(nums)=4,for循环相当于遍历0,1,2,3,4;
3.index必须小于等于max_pos,因为max_pos的值是它能跳到最远的位置;并且index和该位置的值只有大于max_pos时,才能跳到更远的位置,不然就没意义了,比如(index=3,nums=2)、(index=4,nums=0)、(index=5,nums=1),max_pos=4(它位于前者),后者的index + nums[index]也等于4,如果它跳过去游戏也就结束了,因此选择跳到idex=5是更好的选择。这相当于是一个选择的过程,看选择哪一个index会带来最大的资源(max_pos),更新完后max_pos就是新的值了,这在算法中是非常常见的,然后进行新的循环,直至max_pos到达队尾—len(nums)。
个人见解:通过for循环+条件模拟贪心算法—计算较为跳跃,while适合动态规划—比如斐波那契数列
class Solution:
def canJump(self, nums) : #灵活跳
max_pos = 0 #1.初始化当前能跳到最远的位置
for index in range(n): #遍历nums中的每个位置
if index <= max_pos and index + nums[index] > max_pos: #判断index位置是否可跳
max_pos = index + nums[index] #更新max_pos
if index >max_pos: #加上可提前断言结束
return False
return max_pos >= len(nums)-1解法2:
解法1和解法2的关键其实都在于贪心算法,在每次做出选择时都使max_pos获取更大的值,以供下次选择能够拥有更多的资源进行选择。
解法2不同的点在于他利用enumerate()函数将数组重新组合为一个索引序列[(0,2),(1,3),(2,1),(3,1),(4,4)](注意enumerate(nums)类型是enumerate,无法直接打印,同map()一样,导出需要list(..)操作,但是遍历时可直接赋值),便于理解和操作,相比解法2,解法1确实挺费脑子的。
class Solution:
def canjump(self, nums):
max_pos = 0 # 初始化
for index, jump in enumerate(nums): # 以每组形式遍历-index=0,jump=2、index=1,jump=3...
if index <= max_pos and index + jump > max_pos: # 判断idex位置是否可跳
max_pos = index + jump # 更新最远能到达位置
if index > max_pos:
return False
return max_pos >= len(nums)-1三、拓展问题
1、固定跳跃游戏:
题目描述同上,但要求每次固定按位置里边的能量值跳跃,问能否到达数组最后一个位置。
这题是本人的一个脑洞,思路也比上边步数这题简单很多,对于解法1/2的算法稍作变动,因为机器人无法做出选择,只能按照位置里边的数值进行跳跃,少了index + jump > max_pos的限制条件
1.初始化max_pos:所能到达的最远位置
2.通过enumerate()函数给nums建立索引序列列表,index,jump赋值,for循环遍历
3.条件语句,跳的位置是其能跳到的最远的位置,跳完后更新max_pos
4.断言max_pos是否到达队尾
class Solution:
def canjump_fix(self, nums): # 固定跳
max_pos = 0
n = len(nums)-1
for index,jump in enumerate(nums):
if index == max_pos:
max_pos = index+jump
return max_pos >= n2、跳跃游戏Ⅱ(最少步数/次数):
题目描述同上,但保证每次都能到达队尾,要求输出运动最少的步数。
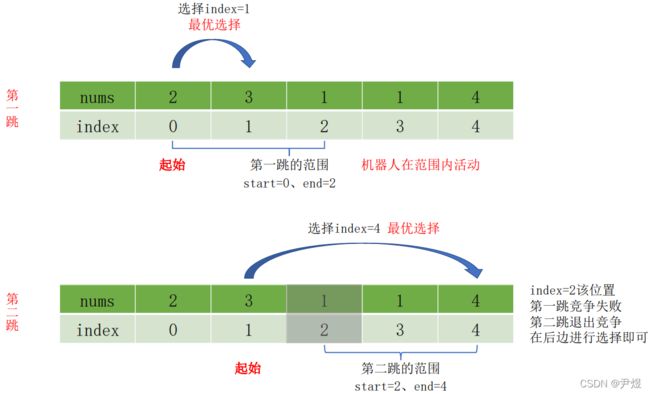
1.方法沿用上边的解法2,因为前边的解法不是最优路径(遍历位置,max_pos每次选择时更进一步,并不是一步到位的),因此增加参数end、start,增加限制条件(在每次选择时给他限制一个范围),同时while循环多次遍历数组,直至能跳出或跳到队尾结束循环。
2.end:边界,每次做出选择时能跳到最远的距离;start:起始位置,每次做出选择时的起始位置;每次while循环时,机器人只能在(start, end + 1)间选择跳哪里,然后在该范围内选择资源最多的位置,因此每次遍历都能跳到资源最多的位置。
3.start,end,step是会随着while循环的次数变化,start请看下边的逻辑,end的值更新,step增加一次,这主要是看while循环的次数。
这里比较绕的可能是两层循环,第一层是while循环,第二层是for循环,比如end=0(初始位置),n=5,①开始第一次while循环,然后for循环对序列(解法2详述)进行遍历,附加三个条件,条件1限制跳的范围,条件2、3确保跳到一个资源更多的位置(也不是一步到位,类似解法1、2),可能进行多次比较后,机器人在范围内跳到了资源最多的位置(index + jump最大),那么可算作一次最优选择,step+1 ②start和end变换位置,这点比较关键,因此做了图方便大家理解,其实start取值<上次选择的den即可,不影响。
class Solution:
def canjump_step(self, nums):
max_pos = 0
start,end,step = 0,0,0 #三参数初始化简化写法
n = len(nums)-1 #因为len()不包含0,和index有冲突,因此-1
while end < n: #跳到最后一位可忽略,不用增加次数
for index, jump in enumerate(nums): #增加一个条件
if index in range(start, end + 1) and\
index <= max_pos and\
index + jump > max_pos:
max_pos = index + jump
start,end,step = end,max_pos,step+1 #参数变化简化写法
return step 3、跳跃游戏Ⅲ(最佳路径)
题目描述同上,也保证每次都能到达队尾,要求输出运动最优的路径。
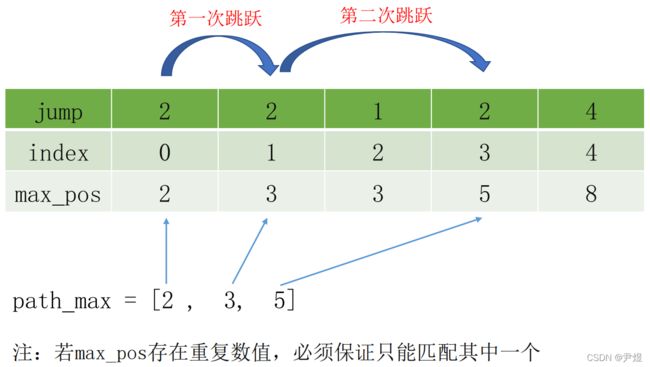
解此题的思路类似跳跃游戏Ⅱ,将步数换成了路径,还是沿用之前的解法,因为每次while循环只能得到选择范围内最大的max_pos,并不能获取跳到了哪个具体位置。但我们能利用这个每次while循环的max_pos,新建一个空的path_max表,将每次while循环后的max_pos填入,这样就得到了机器人的路径的初始表(所走路径上的max_pos=index+jump)。
然后再新建一个空的path表,将path_max表与索引序列里的值进行比对,如下图,实现方法:可先通过for循环遍历path_max,并与索引序列进行比对(index+jump == path_max[i]),如果比对成功使得path_max的遍历起始位置向右移动一位,即可满足。
class Solution:
def canjump_path(self, nums):
max_pos = 0
path_max = []
path = []
start,end,n=0,0,len(nums)-1
while end < n:
for index,jump in enumerate(nums):
if index in range(start,end+1) and\
index <= max_pos and\
index + jump > max_pos:
max_pos = index + jump
start,end = end,max_pos
path_max.append(max_pos)
i = 0
for index, jump in enumerate(nums):
for j in range(i,len(path_max)):
if index+jump == path_max[i]:
path.append(index)
i = i+1
return path总结
困扰好久的跳跃问题终于结束了,大家如果有疑问都可以评论提出,有不足之处请大家批评指正,希望能多结识这方面的朋友,共同学习、共同进步。