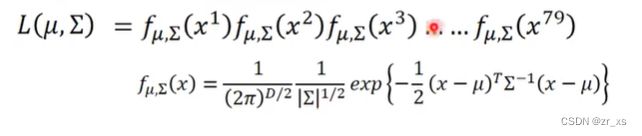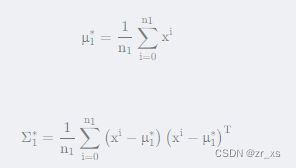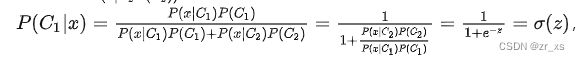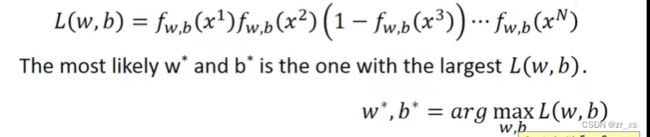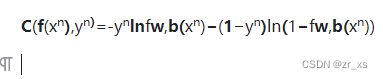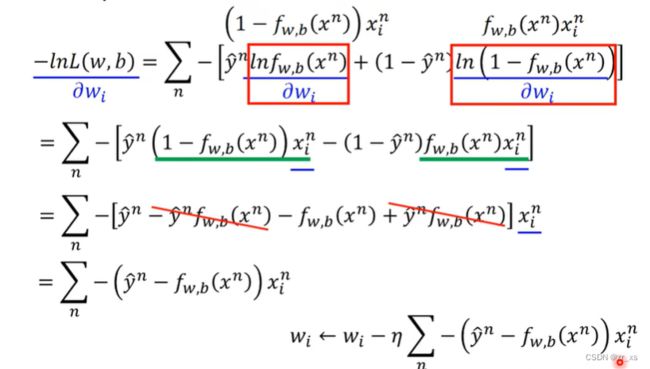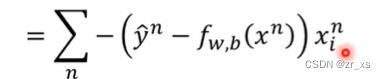机器学习-监督学习-分类
这里推荐一下:机器学习中的数学——常用概率分布(一):伯努利分布(Bernoulli分布)_von Neumann的博客-CSDN博客_bernoulli分布
例如,你的垃圾邮件过滤器是一个机器学习程序,通过学习用户标记好的垃圾邮件和常规非垃圾邮件示例,它可以学会标记垃圾邮件。系统用于学习的示例称为训练集。在此案例中,任务(T)是标记新邮件是否为垃圾邮件,经验(E)是训练数据,性能度量(P) 需要定义。例如,你可以定义正确分类的电子邮件的比例为P。这种特殊的性能度量称为准确度,这是一种有监督的学习方法,常被用于分类任务。
分类是一种基于一个或多个自变量确定因变量所属类别的技术。
逻辑回归类似于线性回归,适用于因变量不是一个数值字的情况 (例如,一个“是/否”的响应)。它虽然被称为回归,但却是基于根据回归的分类,将因变量分为两类。
K-NN算法是一种最简单的分类算法,通过识别被分成若干类的数据点,以预测新样本点的分类。K-NN是一种非参数的算法,是“懒惰学习”的著名代表,它根据相似性(如,距离函数)对新数据进行分类。
支持向量机既可用于回归也可用于分类。它基于定义决策边界的决策平面。决策平面(超平面)可将一组属于不同类的对象分离开。
朴素贝叶斯分类器建立在贝叶斯定理的基础上,基于特征之间互相独立的假设(假定类中存在一个与任何其他特征无关的特征)。即使这些特征相互依赖,或者依赖于其他特征的存在,朴素贝叶斯算法都认为这些特征都是独立的。这样的w理想,朴素贝叶斯因此而得名。
例子:宝可梦的属性分类:
输入:宝可梦数值(血量,攻击力,防御,...........)
输出:宝可梦属性
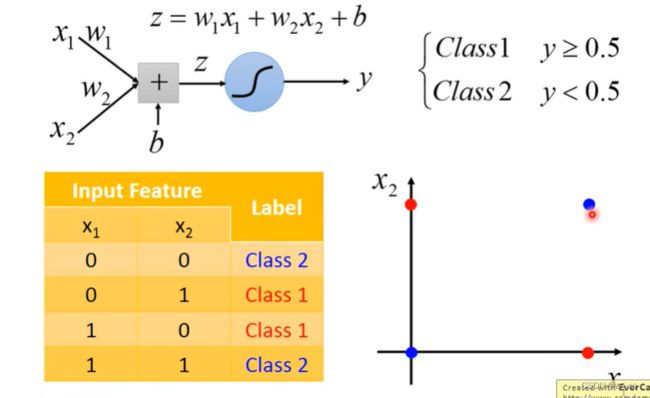
(1)不能把分类当作回归做:
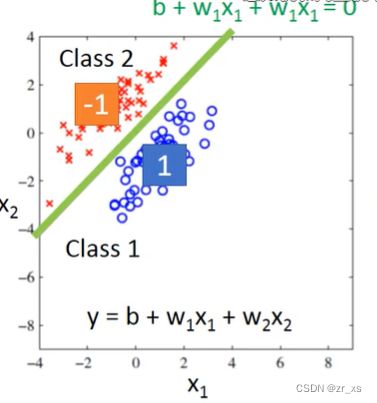
假设用 线性回归来解决: y=b+w1x1+w2k2 ,输入2个影响因素。输出y =值。
假设有两个类别,其中类别1的标签为1,类别2的标签为-1,那0就是分界线,大于0就是类别1,小于0就是类别2。(下面左图)
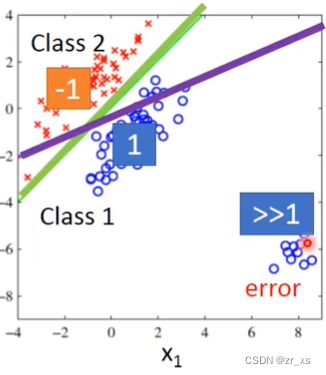
回归模型会惩罚那些太正确的样本。如果结果远远大于1,它的分类应该是类别1还是类别2?这时为了降低整体误差,需要调整已经找到的回归函数,就会导致结果的不准确。
可能遇到(下面右图)那样问题,y>>1。回归得出来的结果是紫色那条,与正确的表达式(绿色)差距较大。感知机的损失函数导致regression总想将所有的样本点考虑进来并最小化二分类损失。
假设有多个类别,类别1的标签是1,类别2的标签是2,类别3的标签是3。
这样的话,标签间具有2和3相近、3大于2这种本来不存在的数字关系。
(2)回归和分类,优化的目标函数不一样。前者是误差之和最小,后者是错分总数最少。机器学习的另一经典问题——分类,与回归的“预测数值”不同,分类需要“预测标签”。
(3)定义 function 与loss损失函数(输入x,输出类别y‘不等于正确类别y的次数总和):
function:模型可以根据特征判断类型,输入是特征,输出是类别
损失函数:预测错误的次数,即 L(f)=∑nδ(f(xn)≠y^n) 。这个函数不可微
如何找到最好的函数,比如感知机(Perceptron)、支持向量机(SVM)
(4)采用朴素贝叶斯算法:
(5)理解贝叶斯定理:3个范例带你读懂贝叶斯法则 - 知乎
假设艾滋病毒HIV在人群中的携带比率为0.01%,目前检测它的医学技术非常高超,如果一个人真的携带有HIV,那么血液检测有99.9%的概率为阳性,即检测出来的概率很高。如果一个人不携带有HIV,那么血液检测只有0.01%的概率为阳性,即冤枉一个正常人的概率很低。现在从街头上随机找个人给他做检查,发现检测结果不妙,是HIV阳性,那么他真的携带有HIV病毒的概率为多大?
从这个例子中,我们发现如果一个事件发生的先验概率很低,那么即使出现了非常有力的证据,这个事件发生的后验概率也不一定会很高。
(6)scikit-learn中朴素贝叶斯类库的使用也比较简单。相对于决策树,KNN之类的算法,朴素贝叶斯需要关注的参数是比较少的。
在scikit-learn中,一共有3个朴素贝叶斯的分类算法类。分别是GaussianNB,MultinomialNB和BernoulliNB。其中GaussianNB就是先验为高斯分布的朴素贝叶斯,MultinomialNB就是先验为多项式分布的朴素贝叶斯,而BernoulliNB就是先验为伯努利分布的朴素贝叶斯。
MultinamialNB这个函数,只有3个参数:alpha(拉普拉斯平滑),fit_prior(表示是否要考虑先验概率),和class_prior:可选参数
MultinomialNB一个重要的功能是有partial_fit方法,这个方法的一般用在如果训练集数据量非常大,一次不能全部载入内存的时候。这时我们可以把训练集分成若干等分,重复调用partial_fit来一步步的学习训练集,非常方便。
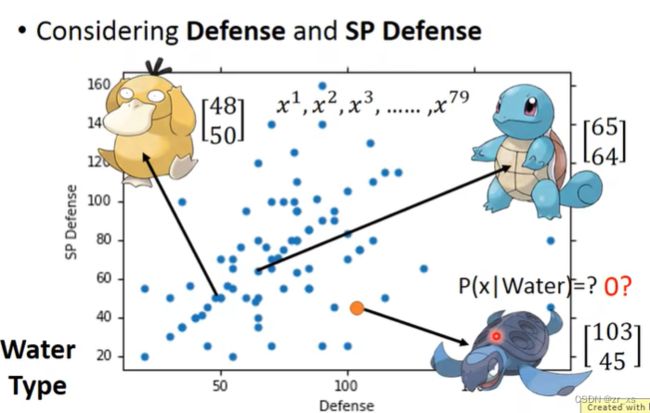
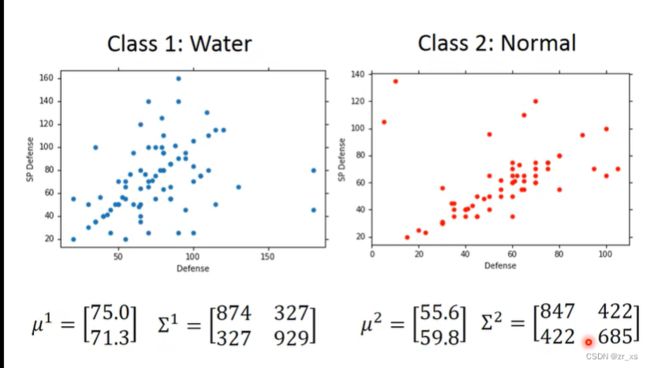
宝可梦分为水系p(c1)、普通系p(c2)。训练集(79水,61普通)
可以根据数据集中属于两个类别的对象的数量计算P(C1)和P(C2)这两个先验概率(Prior Probability):
即 从水系挑一个宝可梦,是海龟几率。
将每一个精灵用一组向量【sp,De】表示。(分别代表防御力,特殊防御力)
(8)
正态分布(Normal distribution)又名高斯分布(Gaussian distribution),是一个在数学、物理及project等领域都很重要的概率分布,在统计学的很多方面有着重大的影响力。
若随机变量X服从一个数学期望为μ、标准方差为σ2的高斯分布,记为:
X∼N(μ,σ2),
正态分布的期望值μ决定了其位置,其标准差σ决定了分布的幅度。因其曲线呈钟形,因此人们又常常称之为钟形曲线。我们通常所说的标准正态分布是μ = 0,σ = 1的正态分布。
(8.1)多维高斯分布 理解多维高斯分布 - 知乎
多维高斯分布其变量为n维变量,每个变量之间可能会存在关系,为了描述这种关系,我们引入了协方差矩阵Σ,其大小为n×n,
(9)计算后验概率(Posterior Probability)P(x|C1)和P(x|C2),可以假设训练集中的各类别样本的特征分别是从某个多元正态分布(多元对应特征的多维)中取样得到的,或者说是假设训练集中各类别样本的特征分别符合某多元正态分布。
找出一个高斯分布,使得其找到所有点的概率都相对来说很大假设高斯分布,利用已有的数据,求得μ ,Σ。
通过极大似然估计(Maximum Likelihood Estimate,MLE),我们可以找到取样得到训练集特征的概率最大的那个正态分布,假设其均值和协方差矩阵为μ∗和Σ∗。
为对应高斯 模拟出这79个点的几率
找到最好的模型,即找出 一组(μ , Σ)让对应高斯 模拟出这79个点的几率最大。
正态分布有2个参数,即均值μ(代表正态分布的中心位置)和协方差矩阵(Covariance Matrix)Σ(代表正态分布的离散程度),计算出均值μ和协方差Σ即可得到该正态分布。
公式中的D为多维特征的维度。
j计算结果
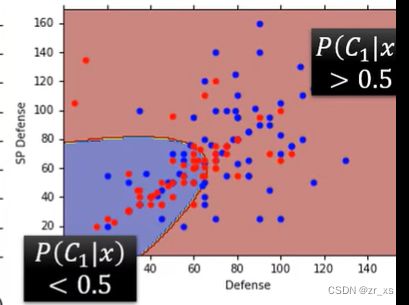
二维空间下分类:(2个参数)
7个参数:
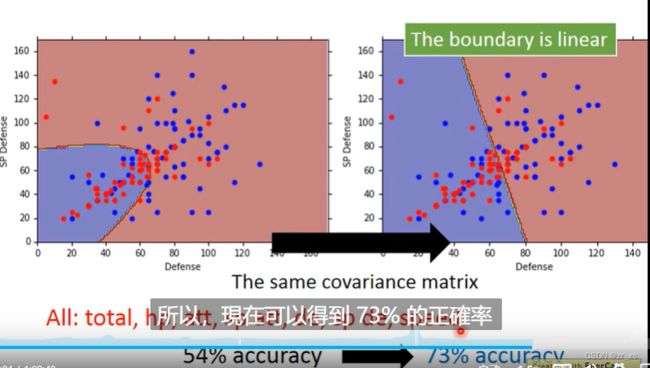
(10)水系和普通系 用同一个协方差。
每个类别(c1,c2)的特征符合一个多元正态分布,每个多元正态分布也有不同的均值和协方差矩阵。让每个类别对应的多元正态分布共享一个协方差矩阵(各个协方差矩阵的加权平均和),公式为Σ=N1N1+N2Σ1+N2N1+N2Σ2,可以减少模型参数,缓解过拟合。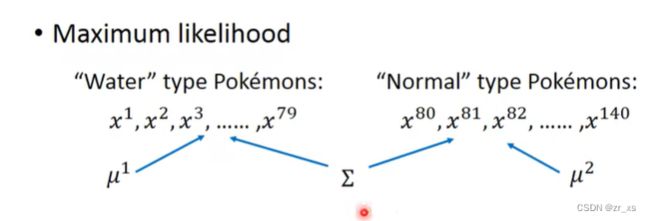
同一个协方差:二维下 右图
7维下:胜率提升到73%
(11)当特征间满足互相独立假设时,不同维特征向量间相关性为0,协方差即为0,只有自己和自己乘积才不为0,所以得到一个对角阵
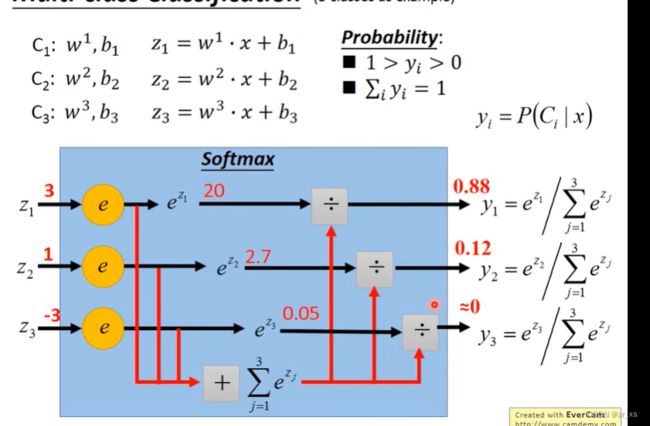
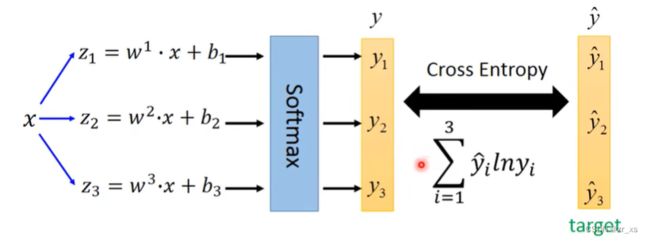
(12)
除了正态分布,还可以用其它的概率模型。
比如对于二值特征,可以使用伯努利分布(Bernouli Distribution)。
朴素贝叶斯分类
如果假设样本各个维度的数据是互相独立的,那这就是朴素贝叶斯分类器(Naive Bayes Classfier)。
(13)一段数学推导:balabala.....
这就是Sigmoid函数。
如果共享协方差矩阵,经过运算可以得到z=wT⋅x+b的形式,其中常量![]() ,常量
,常量![]() ,
,
即形如P(C1|x)=σ(z)=σ(w⋅x+b)。
看起来还是一个 线性模型
---------------------------------------------------------------------------------------------------------------------------------=========================================================================
从概率推导出sigmoid激活的神经网络-
逻辑回归:
Logistic Regression常用于解决二分类问题。
(1)逻辑回归与线性回归:
逻辑回归解决的是回归问题,逻辑回归相当于是线性回归的基础上,来解决分类问题。
线性回归的参数计算方法是最小二乘法,逻辑回归的参数计算方法是似然估计的方法
线性回归(Linear Regression):![]()
逻辑回归:![]()
从上面两个公式:逻辑回归可以理解为在线性回归后加了一个sigmoid函数。将线性回归变成一个0~1输出的分类问题。
sigmoid函数就是:(上面推导出的就是一个sigmoid函数)![]()
函数图像是:
![]()
线性回归得到大于0的输出,逻辑回归就会得到0.5 ~ 1的输出;线性回归得到小于0的输出,逻辑回归就会得到0 ~ 0.5的输出
(2)继续视频:逻辑回归
我们找的是一个几率,根据概率p来决定宝可梦的属性。
(3)伯努利分布
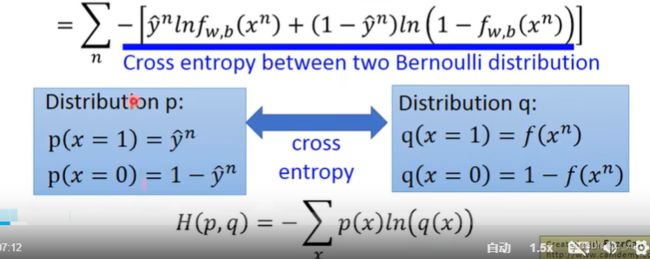
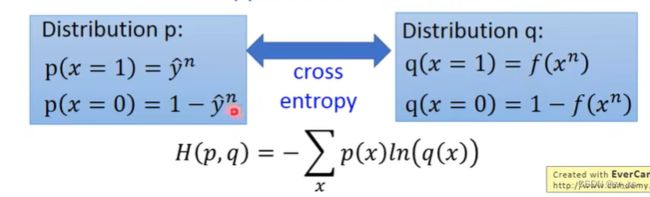
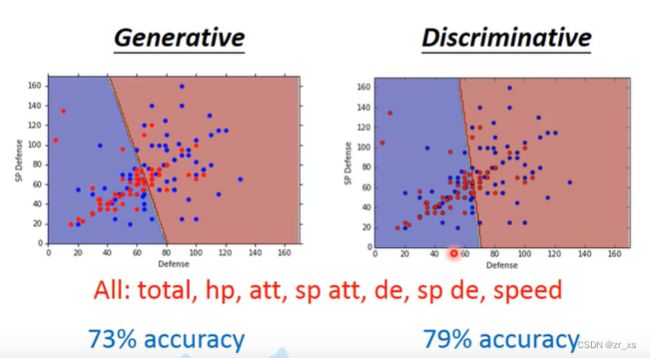
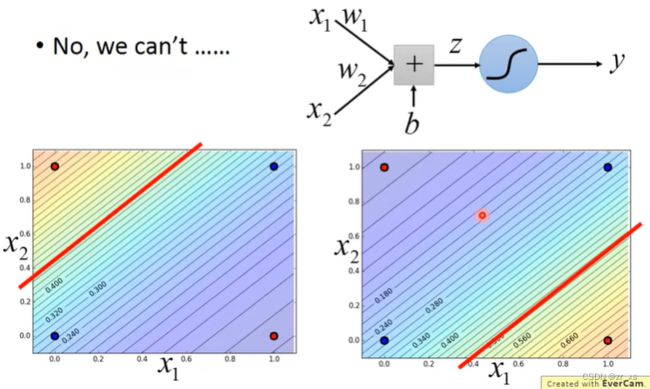
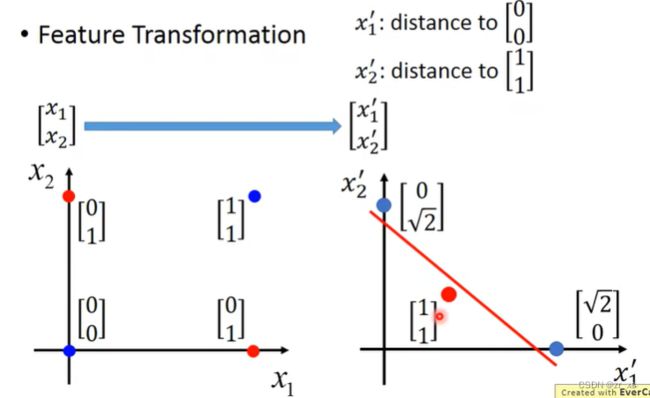
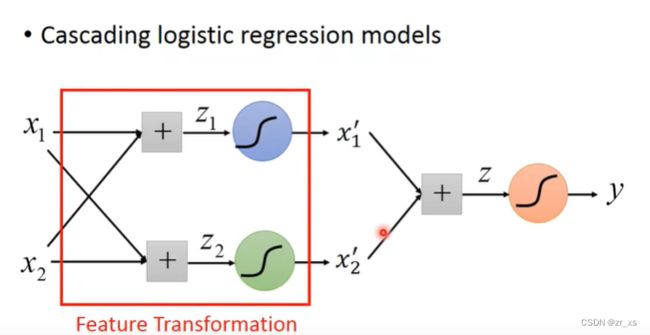
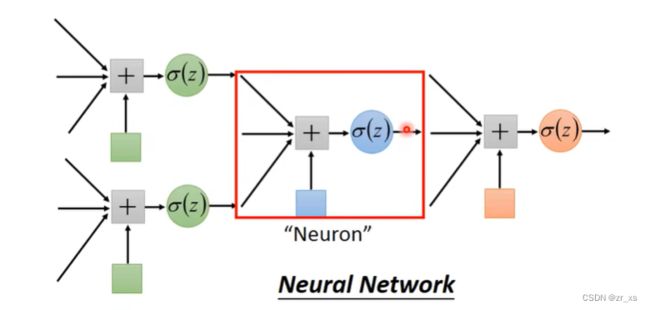
伯努利分布指的是对于随机变量X有, 参数为p(0 (4)比较:线性回归与逻辑回归: 假设我们的训练集是根据 function找出来的。从模型fw,b(x)=Pw,b(C1|x)中取样得到训练集的概率 ---》损失函数 fw,b(x1) 为:该组(w,b)下, x1是水属性(c1)的几率; x3不是c1,是c2;所以几率为(1-fw,b(x3)) 最好的那一组(w,b)就是最大可能产生这组 Training Data。就是让L(w,b)最大 (6)交叉熵(Cross-Entropy) 1.在机器学习中,P往往用来表示样本的真实分布,Q用来表示模型所预测的分布。P、Q分别是真实值和预测值。 如果用P来描述样本,那么就非常完美。而用Q来描述样本,虽然可以大致描述,但是不是那么的完美,信息量不足,需要额外的一些“信息增量”才能达到和P一样完美的描述。如果我们的Q通过反复训练,也能完美的描述样本,那么就不再需要额外的“信息增量”,Q等价于P。 我们需要评估label和predicts之间的差距。一般在机器学习中直接用用交叉熵做loss,评估模型。 如果这两个分布一样的话,KL散度是0,即算出来loss=0,交叉熵等于真实分布的熵 2.机器学习分类模型中会使用交叉熵作损失函数。 (吴恩达的机器学习视频中猫分类器使用的二分类交叉熵建议去看看 损失函数loss: 代入上面: 3.逻辑回归使用均方差损失函数可能效果不好,所以要使用交叉熵作损失函数。 像linear regression一样,用square error: 使用交叉熵: 逻辑回归假设的是概率分布,线性回归假设的是函数值 (7)找一个最好的 函数 ,进行Gradient Descent 让损失函数最小,采用 梯度下降。 (8)discriminative (判别式模型)与generative(生成式模型) 判别模型直接判断一只羊是山羊还是绵羊,而生成模型会先找出山羊特征,再找出绵羊特征,最后再判断这只羊的种类 如果生成模型中共用协方差矩阵,那两个模型/函数集其实是一样的,都是P(C1|x)=σ(w⋅x+b)。 因为做了不同的假设,即使是使用同一个数据集、同一个模型,找到的函数是不一样的。 是2个参数(看不出来优劣);和7个参数(73%,79%) 判别模型是看着数据说话,没有它自己的假设,受数据量的影响较大 生成模型是有它自己的假设。 如果训练数据比较少,则使用生成式可能效果更好。 (9)衍生到多分类: ------------- 假设分3个类别:class1 class2 class3 在机器学习尤其是深度学习中,softmax是个非常常用而且比较重要的函数,尤其在多分类的场景中使用广泛。他把一些输入映射为0-1之间的实数,并且归一化保证和为1,因此多分类的概率之和也刚好为1。 入门级都能看懂的softmax详解_bitcarmanlee的博客-CSDN博客_softmax函数 yi =P(ci|x),拿到一个x,属于ci类的概率 目前看到的大多数特征工程方法都是针对数值特征的。本文介绍的Target Encoding是用于类别特征的。这是一种将类别编码为数字的方法,就像One-hot或Label-encoding一样,但和这种两种方法不同的地方在于target encoding还使用目标来创建编码,这就是我们所说的有监督特征工程方法。Target Encoding是任何一种可以从目标中派生出数字替换特征类别的编码方式。 target encoding的缺点主要有: 鉴于以上缺点的存在,一般会加入平滑来进行处理。 在数据分析之前,我们通常需要先将数据标准化(normalization),利用标准化后的数据进行数据分析。数据标准化处理主要包括数据同趋化处理和无量纲化处理两个方面。 把特征的各个维度标准化到特定的区间 把有量纲表达式变为无量纲表达式 ================================================================================================================================================== (1).逻辑回归的限制: 2个输入(x1,x2) ,输出 label。2维对应是一条直线 无论怎么改变w1 w2 b 的值都不能 用一条线划分 2个class (2)转化 将x1'定义为到点(0,0)的距离 将x2'定义为到点(1,1)的距离 (3)怎么让机器自己知道 产生这种转换: x1,x2 输入到新的model1 得到x1‘ x1,x2 输入到新的model2 得到x2‘ 输入x1’ x2‘ 到model3,可以进行分类,万事大吉 每一个 逻辑回归模型 叫 神经元;将他们串起来叫神经网络
这一节的logistic regression 是属于discriminative (判别式模型),而上一节中用高斯分布描述数据的联合概率的方法求model属于generative(生成式模型)。
对于本章来说,左边是直接去寻找W和b,而右边是先假设是高斯分布,再去找的W和b。所以可能是左右两边是不同的W和b。
模型相同,方法不同
判别方法:通过梯度下降,直接找到w,b。
生成方法:通过假设估计N1,N2,μ1,μ2,∑ 来得到w,b 。
同样的模型,同样的训练数据,采用两种方法所得结果(w,b)不同。因为生成模型对概率分布事先做了假设。所以一般来说,Discriminative model会比Generative model表现更好。
生成模型在一些情况下相对判别模型是有优势的:
1、训练数据较少时。判别模型的表现受数据量影响较大,而生成模型受数据量影响较小。
2、label有噪声时。生成模型的假设(“脑补”)反而可以把数据中的问题忽视掉。
3、判别模型直接求后验概率,而生成模型将后验概率拆成先验和似然,而先验和似然可能来自不同来源。
过度到 神经网络