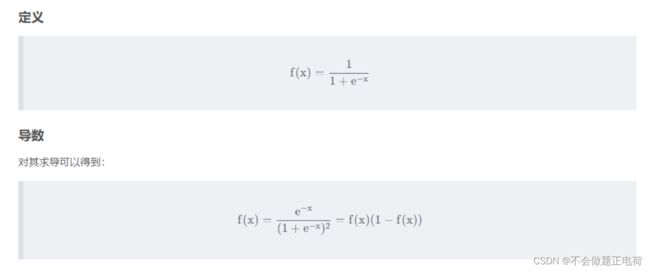机器学习Day3-GNN基础

激活函数

Sigmod

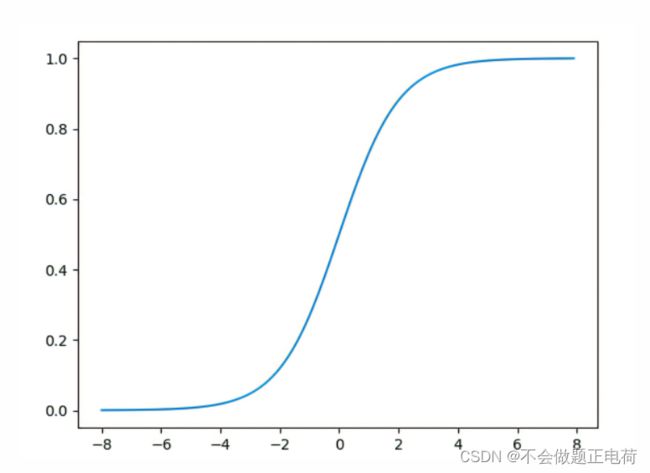
sigmod的函数是一个在生物学中常见的S型函数，也称为S型生长曲线。在信息科学中，由于其单增以及反函数单增等性质，常被用作神经网络的激活函数，将变量映射到0,1之间。sigmod函数也叫作Logistic函数，用于隐层神经单元输出，取值范围为（0,1），它可以将一个实数映射到（0,1）的区间，可以用来做二分类。在特征相差比较复杂或者相差不是特别大的时候效果比较好。

 

 

激活函数

激活函数是神经网络中极为重要的一个概念，它决定了某个神经元是否被激活，这个神经元接受到的信息是否有用，是该留下还是该抛弃掉。在神经网络中我们需要一个机制来区分有用信息和无用信息，类似于大脑中的神经元，有的神经对于某些信号是敏感的而有些神经元对这些信号是抑制的，在神经网络中能起到这个作用的就是激活函数。 实际上，激活函数可以看作是变量间的一个非线性变换，通过引入激活函数来增加神经网络模型的非线性，以便增加对样本非线性关系的拟合能力（在现实生活中，大部分的数据都是线性不可分的）。只有加入了激活函数之后，深度神经网络才具备了分层的非线性映射学习能力。

如果不用激励函数，在这种情况下，你每一层节点的输入都是上层输出的线性函数，很容易验证，无论神经网络有多少层，输出都是输入的线性组合，与没有隐藏层的效果相当，这种情况下就是最原始的多层感知机了（MLP），那么网络的逼近能力就相当有限。而现实生活中大部分的数据都不是线性可分的，正是因为这样，才引入了非线性的函数作为激活函数，这样深层神经网络表达能力就更加强大了。（不再是输入的线性组合，而是几乎可以逼近的任意函数。）

sigmod作为激活函数的时候存在的问题

1.当很多个使用sigmoid激活函数的Layers 加到神经网络中时，损失函数的梯度会接近0，这会导致 network难以训练。因为通过上图可以看出，当输入值很小或者很大的时候，sigmod的梯度都会趋向于0，而我们经常使用梯度乘以学习率来更新权值函数的，所以会导致权值改变非常小，难以训练。

2.通过问题1 可以知道你需要尤其注意参数的初始值来尽量避免saturation（饱和，即梯度趋于0）的情况。也就是说对初始值是有所限制的。（其实，纵使是限制了，对于层数较多的神经网络来说，效果也不是特别好。）

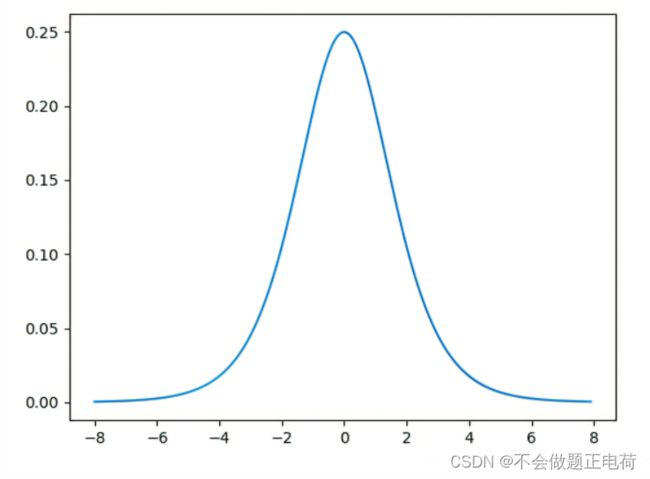
3.会导致梯度消失或者梯度爆炸。如果是只有几个sigmoid层的浅层神经网络,这并不会引起很大的问题。然而，当非常多的sigmoid层时，就会产生问题。通常我们会初始化参数的值在（0,1）之间，通过sigmod的导数图像来看，当输入在（0,1）之间的时候，梯度值大约在（0.2-0.25）之间（可以将图像放大来看，如下图）。由反向传播算法的数学推导可知，梯度从后向前传播时，每传递一层梯度值都会减小为原来的0.25倍，如果神经网络隐层特别多，那么梯度在穿过多层后将变得非常小接近于0，即出现梯度消失现象；当网络权值初始化为 (1,+∞) 区间内的值，则会出现梯度爆炸情况，梯度爆炸的情况还是比较少见的。推导如下，或者参见这里。

神经网络的梯度通过反向传播来得到，简单的说，反向传播通过从最终层到初始层，误差逐层传播来得到梯度，通过链式求导法则，每一层的导数会乘到一起来计算初始层的导数。

4.Sigmoid 的 output 不是0均值. 这是不可取的，因为这会导致后一层的神经元将得到上一层输出的非0均值的信号作为输入。 产生的一个结果就是：如果数据进入神经元的时候是正的(e.g. elementwise in )，那么 计算出的梯度也会始终都是正的。 为了解决sigmod这种问题，后面出现了Thah、Relu等激活函数。

损失函数

损失函数就一个具体的样本而言，模型预测的值与真实值之间的差距。 对于一个样本（xi,yi）其中yi为真实值，而f（xi）为我们的预测值。使用损失函数L（f(xi),yi）来表示真实值和预测值之间的差距。两者差距越小越好，最理想的情况是预测值刚好等于真实值。

梯度

百度上面：梯度的本意是一个向量（矢量），表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大（为该梯度的模）。 梯度下降：简单说就是从山顶上找一个最快，最陡峭的路线下山

机器学习/深度学习中，需要使用训练数据来最小化损失函数，从而确定参数的值。而最小化损失函数，即需要求得损失函数的极值。 求解函数极值时，需要用到导数。对于某个连续函数f ( x )，令其一阶导数 f ′ ( x ) = 0，通过求解该微分方程，便可直接获得极值点。但当变量很多或者函数很复杂时，f ′ ( x ) = 0 的显式解并不容易求得。且计算机并不擅长于求解微分方程。 计算机所擅长的是，凭借强大的计算能力，通过插值等方法（如牛顿下山法、弦截法等），海量尝试，一步一步的去把函数的极值点“试”出来。而海量尝试需要一个方向感，为了阐述这个方向感，介绍一下方向导数。

方向导数

方向导数是偏导数的概念的推广, 偏导数研究的是指定方向 (坐标轴方向) 的变化率，到了方向导数，研究哪个方向可就不一定了。 函数在某一点处的方向导数在其梯度方向上达到最大值，此最大值即梯度的范数。

梯度

在一个数量场中，函数在给定点处沿不同的方向，其方向导数一般是不相同的。那么沿着哪一个方向其方向导数最大，其最大值为多少，这是我们所关心的，为此引进一个很重要的概念: 梯度。 函数在某一点处的方向导数在其梯度方向上达到最大值。 这就是说，沿梯度方向，函数值增加最快。同样可知，方向导数的最小值在梯度的相反方向取得，此最小值为最大值的相反数，从而沿梯度相反方向函数值的减少最快。

梯度值

在单变量的实值函数中，梯度可简单理解为只是导数，或者说对于一个线性函数而言，梯度就是曲线在某点的斜率。 对于多维变量的函数，比如在一个三维直角坐标系，该函数的梯度就可以表示为公式

为求得这个梯度值，要用到“偏导”的概念。

γ 在机器学习中常被称为学习率 ( learning rate )， 也就是上面梯度下降法中的步长。 通过算出目标函数的梯度（算出对于所有参数的偏导数）并在其反方向更新完参数 Θ ，在此过程完成后也便是达到了函数值减少最快的效果，那么在经过迭代以后目标函数即可很快地到达一个极小值。如果该函数是凸函数，该极小值也便是全局最小值，此时梯度下降法可保证收敛到全局最优解。梯度下降由梯度方向，和步长决定，每次移动一点点。但是每一次移动都是对你所在的那个点来说，往极值方向，所以能够保证收敛。

Graph Network

有向图

无向图

连通分量：无向图G中的一个极大连通子图称为G的一个连通分量，连通图只有一个连通分量，就是他本身，非连通图的无向图有多个连通分量

度：出度和入度

连通图

非连通图

强连通图：任意两个结点，至少存在一条路径可以从u开始，到结点v结束

弱连通图：至少有一对结点不满足单向连通

图直径：所有最短路径之间的最大值

度中心性：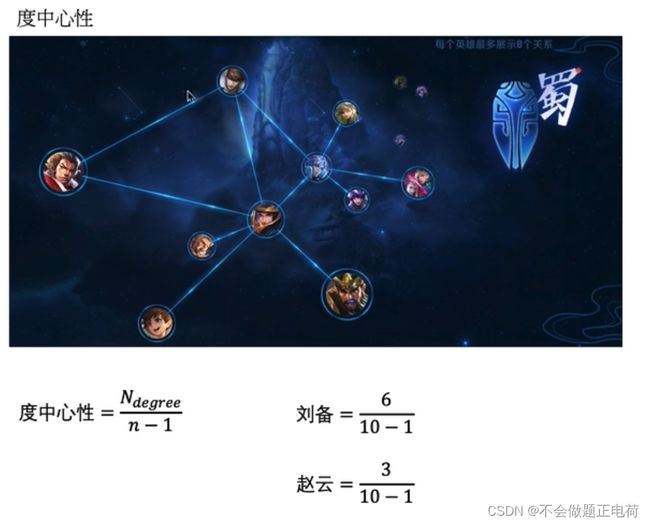

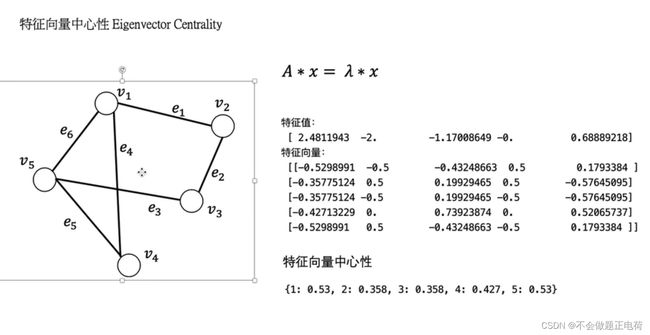
特征向量中心性

EIGENVECTOR CENTRALITY

中介中心性

BEWTWEENNESS CENTRALITY

连接中心性Closeness

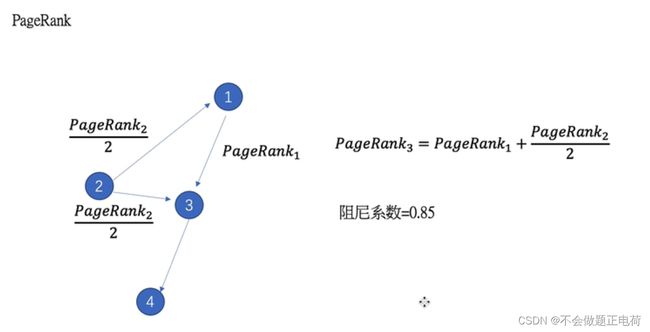
PageRank

页面排序算法：

有1-阻尼系数的概率可以到达非目标节点

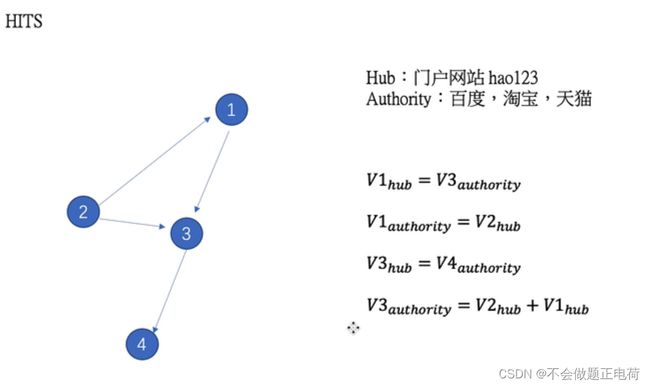
HITS

Hub结点：门户网站

Authority结点：百度、淘宝、天猫

每一个结点都有一个Hub和Authority值

代码

import networkx as nx
import pandas as pd 
import numpy as np
​
edges=pd.DataFrame()
edges['sources']=[]
edges['targets']=[]
edges['weights']=[]
​
G=nx.from_pandas_edgelist(edges,source='sources',target='targets',edge_attr='weights')
#degree
#连通分量
#图直径...都可以通过函数直接求出

Graph Embedding

有n维one-hot向量，简化节点特征长度，保留节点在图上的信息。

为什么我们要使用图形嵌入?

需要使用图形嵌入有以下几个原因:

机器学习图形是有限的。图由边和节点组成。这些网络关系只能使用数学、统计和机器学习的特定子集，而向量空间有更丰富的方法工具集。

嵌入是压缩的表示。邻接矩阵描述图中节点之间的连接。它是一个|V| x |V|矩阵，其中|V|是图中节点的个数。矩阵中的每一列和每一行表示一个节点。矩阵中的非零值表示两个节点相连。使用邻接矩阵作为大型图的特征空间几乎是不可能的。假设一个图有1M个节点和一个1M x 1M的邻接矩阵。嵌入比邻接矩阵更实用，因为它们将节点属性打包到一个维度更小的向量中。

向量运算比图形上的可比运算更简单、更快。

DeepWalk

随机游走采样获得图上的信息，降低维度

随机游走：按照边可以进行随机游走，得到每一个节点的随机游走序列。训练出每一个结点embedding的表示

在已经知道Label的基础上，首先无监督的学习，训练出embedding的表示，使用embedding的表示作为特征输入到分类器中去判断embedding的好坏，以此检验（有监督）。

图-学习知识

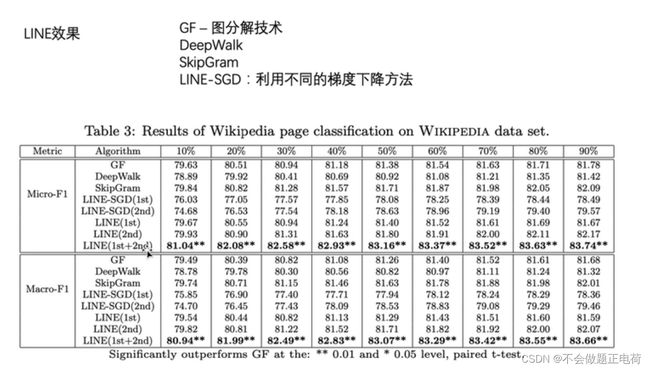
LINE

LINE在适用于大规模的图上，表示节点之间的结构信息

一阶：局部的结构信息

二阶：节点的邻居，共享邻居的节点可能是相似的

DeepWalk在无向图上，LINE在有向图上可以使用

其中exp()就是e的多少次方，如：exp(2)=e^2

一阶和二阶直接拼接即可

 

作者提出的LINE方法的效果是对比组中最好的。

Kullback-Leibler差异

相对熵：衡量相同时间空间里，两个概率分布相对差距的测度。

• 两个概率分布的差距越大，KL距离越大；

• 当两个概率分布相同时，KL距离为0

其中，p ( x ）与q ( x ) 是两个概率分布。