m通信系统中基于相关峰检测的信号定时同步算法的FPGA实现
目录
1.算法描述
2.仿真效果预览
3.verilog核心程序
4.完整FPGA
1.算法描述
定时同步方法主要分为基于数据辅助和非数据辅助两类。前者是在发送有效数据前发送一段具有某种特征的训练或导频符号,接收端根据符号特征建立同步,具有同步建立速度快、精度高的特点,适用于分组通信或突发通信系统;后者典型的是利用循环前缀进行同步估计,不需要插入训练符号,传输效率高,但同步捕获时间长,精度较差,通常仅适用于连续传输系统。由于实际中常用的无线通信系统大多属于分组通信或突发通信,多采用基于训练序列的定时同步方法,因此本文主要对该同步方法进行分析研究和工程实现。首先对基于训练序列的定时同步原理和同步序列的设计进行简要介绍,其次对同步序列的性能进行仿真分析,然后详细阐述定时同步模块的结构设计,最后利用FPGA编程实现并进行综合仿真,验证该设计的可行性。
定时同步在实际中一般比较复杂,本文,我们主要使用加入的帧头信息进行定时同步,由于接收和发送是两块板子,所以他们对应的晶振是不同的,所以两个晶振之间会存在细微的频率差,这就是时偏,利用本方案加入的帧头,对每帧数据进行采样时钟的刷新,从而实现一帧之内采样时钟的偏差不超过一个时钟周期。
帧头信息采用PN码,PN码序列捕获指接收机在开始接收扩频信号时,选择和调整接收机的本地扩频PN序列相位,使它与发送的扩频PN序列相位基本一致,即接收机捕捉发送的扩频PN序列相位,也称为扩频PN序列的初始同步。在系统接收端,一般解扩过程都在载波同步前进行,实现捕获大多采用非相干检测。接收到扩频信号后,经射频宽带滤波放大及载波解调后,分别送往2N扩频PN序列相关处理解扩器(N是扩频PN序列长)。2N个输出中哪个输出最大,该输出对应的相关处理解扩器所用的扩频PN序列相位状态,就是发送的扩频信号的扩频PN序列相位,从而完成扩频PN序列捕获。捕获的方法有多种,如滑动相干法、序贯估值法及匹配滤波器法等,滑动相关法是最常用的方法。
2.1 滑动相关法
接收系统在搜索同步时,它的码序列发生器以与发射机码序列发生器不同的速率工作,致使这两个码序列在相位上互相滑动,只有在达到一致点时,才停下来,因此称之为滑动相关法。接收信号与本地PN码相乘后积分,求出它们的互相关值,然后与门限检测器的某一门限值比较,判断是否已捕获到有用信号。它利用了PN码序列的相关徨性,当两个相同的码序列相位一致时,其相关值输出最大。一旦确认捕获完成,捕获指示信号的同步脉冲控制搜索控制钟,调整PN码发生器产生的PN码重复频率和相位,使之与收到的信号保持同步。由于滑动相关器对两个PN码序列按顺序比较相关,所以该方法又称顺序搜索法。滑动相关器简单,应用簋广,缺点是当两个PN码的时间差或相位差过大时,相对滑动速度簋慢,导致搜索时间过长,特别是对长PN码的捕获时间过长,必须采取措施限定捕获范围,加快捕获时间,改善其性能。
2.2 序贯估值法
序贯估值法是另一种减少长码捕获时间的快速捕获方法,它把收到的PN码序列直接输入本地码发生器的移位寄存器,强制改变各级寄存器的起始状态,使其产生的PN码与外来码相位一致,系统即可立即进行同步跟踪状态,缩短了本地PN码与外来PN码相位一致所需的时间。该方法先检测收到码信号中的PN码,通过开关,送入n级PN码发生器的移位寄存器。待整个码序列全部进入填满后,在相关器中,将产生的PN码与收到的码信号进行相关运算,在比较器中将所得结果与门限进行比较。若未超过门限,则继续上述过程。若超过门限,则停止搜索,系统转入跟踪状态。理想情况下,捕获时间Ts=nTc,(Tc为PN码片时间宽度)。该方法捕获时间虽短,但存在一些问题,它先要对外来的PN码进行检测,才能送入移位寄存器,要做到这一点有时很困难。另外,此法抗干扰能力很差,因为逐一时片进行估值和判决,并未利用PN码的抗干扰特性。但在无干扰条件下,它仍有良好的快速初始同步性能。
2.3 匹配滤波器法
用于PN同步捕获的匹配滤波器一般采用延时线匹配滤波器,其目的是识别码序列,它能在特殊结构中识别特殊序列,而且只识别该序列。假设一个输入信号是7bit码序列1110010双相调制的信号,每当码有1-0过渡时,反相信号进入延时线,直到第1bit在T7,第2bit在T6。当全部时延元件都填满,而且信号调制码与滤波器时延元件相位一致时,T2的信号相位与T5、T6、T7的相位相同,时延元件T1、T3、T4也具有相同的信号相位。把{T2、T5、T6、T7}与{T1、T3、T4}两组分别相加,把{T1、T3、T4}之和倒相输出,再将这两个结果相加,包含在全部7个元件中的信号能量同相相加,整个输出是未处理的7倍。根据该能量关系可以识别码序列。
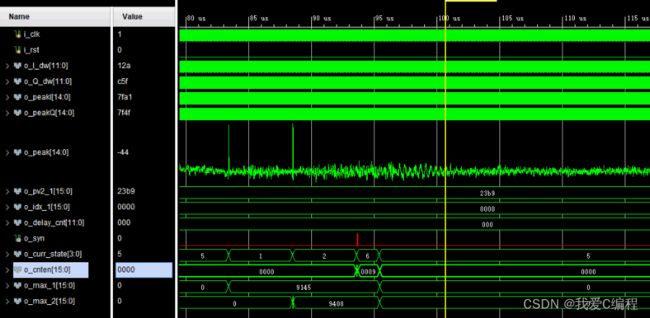
2.仿真效果预览
vivado2019.2仿真结果如下:
3.verilog核心程序
always @(posedge i_clk or posedge i_rst)
begin
if(i_rst)
begin
for(i=1;i<=32;i=i+1)
dly1[i]<={(WTH+2){1'b0}};
for(i=1;i<=8;i=i+1)
dly2[i]<={(WTH+4){1'b0}};
for(i=1;i<=2;i=i+1)
dly3[i]<={(WTH+6){1'b0}};
o_peak<={(WTH+6){1'b0}};
end
else begin
dly1[1] <= dly_peaks[1*SAMP] + dly_peaks[2*SAMP] + dly_peaks[3*SAMP] + dly_peaks[4*SAMP];
dly1[2] <= dly_peaks[5*SAMP] + dly_peaks[6*SAMP] + dly_peaks[7*SAMP] + dly_peaks[8*SAMP];
dly1[3] <= dly_peaks[9*SAMP] + dly_peaks[10*SAMP] + dly_peaks[11*SAMP] + dly_peaks[12*SAMP];
dly1[4] <= dly_peaks[13*SAMP] + dly_peaks[14*SAMP] + dly_peaks[15*SAMP] + dly_peaks[16*SAMP];
dly1[5] <= dly_peaks[17*SAMP] + dly_peaks[18*SAMP] + dly_peaks[19*SAMP] + dly_peaks[20*SAMP];
dly1[6] <= dly_peaks[21*SAMP] + dly_peaks[22*SAMP] + dly_peaks[23*SAMP] + dly_peaks[24*SAMP];
dly1[7] <= dly_peaks[25*SAMP] + dly_peaks[26*SAMP] + dly_peaks[27*SAMP] + dly_peaks[28*SAMP];
dly1[8] <= dly_peaks[29*SAMP] + dly_peaks[30*SAMP] + dly_peaks[31*SAMP] + dly_peaks[32*SAMP];
dly1[9] <= dly_peaks[33*SAMP] + dly_peaks[34*SAMP] + dly_peaks[35*SAMP] + dly_peaks[36*SAMP];
dly1[10] <= dly_peaks[37*SAMP] + dly_peaks[38*SAMP] + dly_peaks[39*SAMP] + dly_peaks[40*SAMP];
dly1[11] <= dly_peaks[41*SAMP] + dly_peaks[42*SAMP] + dly_peaks[43*SAMP] + dly_peaks[44*SAMP];
dly1[12] <= dly_peaks[45*SAMP] + dly_peaks[46*SAMP] + dly_peaks[47*SAMP] + dly_peaks[48*SAMP];
dly1[13] <= dly_peaks[49*SAMP] + dly_peaks[50*SAMP] + dly_peaks[51*SAMP] + dly_peaks[52*SAMP];
dly1[14] <= dly_peaks[53*SAMP] + dly_peaks[54*SAMP] + dly_peaks[55*SAMP] + dly_peaks[56*SAMP];
dly1[15] <= dly_peaks[57*SAMP] + dly_peaks[58*SAMP] + dly_peaks[59*SAMP] + dly_peaks[60*SAMP];
dly1[16] <= dly_peaks[61*SAMP] + dly_peaks[62*SAMP] + dly_peaks[63*SAMP] + dly_peaks[64*SAMP];
dly1[17] <= dly_peaks[65*SAMP] + dly_peaks[66*SAMP] + dly_peaks[67*SAMP] + dly_peaks[68*SAMP];
dly1[18] <= dly_peaks[69*SAMP] + dly_peaks[70*SAMP] + dly_peaks[71*SAMP] + dly_peaks[72*SAMP];
dly1[19] <= dly_peaks[73*SAMP] + dly_peaks[74*SAMP] + dly_peaks[75*SAMP] + dly_peaks[76*SAMP];
dly1[20] <= dly_peaks[77*SAMP] + dly_peaks[78*SAMP] + dly_peaks[79*SAMP] + dly_peaks[80*SAMP];
//=====================================================
dly2[1] <= dly1[1]+dly1[2]+dly1[3]+dly1[4];
dly2[2] <= dly1[5]+dly1[6]+dly1[7]+dly1[8];
dly2[3] <= dly1[9]+dly1[10]+dly1[11]+dly1[12];
dly2[4] <= dly1[13]+dly1[14]+dly1[15]+dly1[16];
dly2[5] <= dly1[17]+dly1[18]+dly1[19]+dly1[20];
dly2[6] <= dly1[21]+dly1[22]+dly1[23]+dly1[24];
dly2[7] <= dly1[25]+dly1[26]+dly1[27]+dly1[28];
dly2[8] <= dly1[29]+dly1[30]+dly1[31]+dly1[32];
dly3[1]<=dly2[1]+dly2[2]+dly2[3]+dly2[4];
dly3[2]<=dly2[5]+dly2[6]+dly2[7]+dly2[8];
o_peak<=dly3[1]+dly3[2];
`timescale 1ns / 1ps
module corrpeak_cal_tops(
i_clk,
i_rst,
o_I_dw,
o_Q_dw,
o_peakI,
o_peakQ
);
input i_clk;
input i_rst;
output signed[11:0]o_I_dw;
output signed[11:0]o_Q_dw;
output signed[14:0]o_peakI;
output signed[14:0]o_peakQ;
bignoise_signal signal_u(
.i_clk (i_clk),
.i_rst (i_rst),
.o_I_dw(o_I_dw),
.o_Q_dw(o_Q_dw)
);
corrpeak_cal corrpeak_cal_u1(
.i_clk (i_clk),
.i_rst (i_rst),
.i_base_signal(o_I_dw[11:4]),
.o_peak (o_peakI)
);
corrpeak_cal corrpeak_cal_u2(
.i_clk (i_clk),
.i_rst (i_rst),
.i_base_signal(o_Q_dw[11:4]),
.o_peak (o_peakQ)
);
endmodule
01_205m4.完整FPGA
V