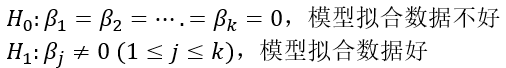python 回归去掉共线性_SAS系列33：SAS高级统计（二）多元线性回归

导读

      上一期介绍了多因素分析方法类型、用途、注意事项。今天我们开始介绍多因素分析中最基本、最常用的方法——多元线性回归分析。

---

一、多元线性回归模型

(一)多元线性回归的数学模型及其基本原理    

       26期我们介绍的简单线性回归分析研究一个反应变量与一个自变量之间的线性依存关系，而多元线性回归分析是简单线性回归分析的扩展形式，是研究一个反应变量与多个自变量之间的线性依存关系。如果应变量y和自变量x1，x2，x3，…，xk有如下线性关系：

则称式11-1为应变量y在自变量上的k元线性回归模型，式中β0为截距，βj(j=1,2,…,k)为偏回归系数，表示x1每改变一个单位时，y的改变量；ε为误差或残差，模型假定误差ε独立且服从均值为0方差为σ2的正态分布。通过一组实际观察数据，可求出式11-1中的参数βj的估计值bj，从而建立经验回归方程：

式11-2中是在自变量x1，x2，x3，…，xk条件下对观察值y的平均估计值，又称平均值。

       多元线性回归分析是应用一个数学模型来提示总体中若干个自变量与一个因变量之间的线性依存关系，并评估用这个数学模型模拟相关事物变化规律的准确性。多元线性回归分析可以从统计意义上确定在消除了其它自变量的影响后，每一个自变量对因变量的影响，并估计出在其他自变量固定不变的情况下，每一个自变量对因变量的数值影响大小。

(二)多元线性回归分析的前提条件       

       对于多元线性回归分析，要求观察数据和模型的残差满足以下前提条件：

      ♦ 因变量y是连续型随机变量，且服从正态分布；如果不满足会导致统计检验结果出现偏倚。

      ♦ 自变量是固定变量，即非随机变量或无度量误差的变量；如果不满足会导致结果失真。

      ♦ 自变量之间不存在多重共线性，即，一些自变量间存在较强的线性关系；如果不满足会导致结论的不唯一性。

      ♦ 自变量与残差独立；如果不满足说明模型中缺少重要自变量。

      ♦ 残差是随机变量，且均值为零，方差为常数s2；如果不满足会导致参数估计出现偏倚。

      ♦ 残差ei之间相互独立；如果不满足会导致结果出现误导。

      ♦ 残差服从正态分布；如果不满足会导致统计检验结果出现偏倚。

(三)多元线性回归分析的步骤      

1. 估计参数

       多元线性回归模型的参数估计方法有普通最小二乘法、最大似然法和矩估计。一般情况下，采用的是最小二乘法，即使得残差平方和最小的方法。令参数βj的估计值bj，bj为偏回归系数。对于多元线性回归分析，除了估计偏回归系数外，还要判断哪一个自变量对因变量的影响最大。由于各自变量的单位不同，因此不能直接用偏回归系数来解释各自变量的重要性。为了去年量纲的影响，可以应用以下两种方法将偏回归系数标准化：

       ♦ 将原始变量标准化后再进行回归，得到的就是标准偏回归系数；

       ♦ 将估计的bj偏回归系数除以因变量y的标准差s，再乘以该系数对应的自变量的标准差。

       偏回归系数没有消除量纲的影响，在同一模型中的偏回归系数估计值不能相互比较，在不同的模型中可以进行比较；标准回归系数估计值消除了量纲的影响，本身没有实际意义，不能直接解释自变量与因变量间的依存关系，也不能在不同模型中进行比较，但是可以在同一模型中对参数估计值进行比较。

2. 检验参数

       对于式11-2中k个自变量(j=1,2,…,k，)，利用偏回归系数估计值bj以及bj的标准误，可以对所有模型参数进行统计假设检验：

3. 检验总体模型

       多元线性回归模型的总体检验应用方差分析，即因变量y的总体变异可以被分解为两部分：一部分是由回归引起的变异；另一部分是由残差引起的变异，即不能由回归模型解释的部分。对模型总体检验的统计假设：

多元线性回归分析也可以得到拟合回归模型的复确定系数R²  ，它表示因变量y的总变异被所有自变量x所能解释的总分占的比例，反映所有自变量与因变量的线性相关强度。

4.模型诊断

       模型诊断是分析实际样本数据与拟合的回归模型之间的拟合情况，通过一些诊断统计量来检测数据、模型与推断过程中可能存在的不合理性，并提出相应解决方案的过程。多元线性回归分析的模型诊断一般包括以下几个部分：

     (1)自变量之间是否存在多重共线性

  多元线性回归模型的多重共线性可用容忍度(tolerance)、方差膨胀因子(variance inflation factor)和最大条件指数(condition number)进行诊断。自变量x_j的容忍度tol=1-R²，其变化范围是0到1之间，当tol(x_j)=0，则该自变量x_j与其它的x变量有相当严重的多重共线性；如果tol(x_j)=1，则该自变量x_j与其它的x变量完全独立。

  方差膨胀因子等容忍度的倒数，即vif(x_j)= 1/tol(x_j)，当vif(x_j)=1时，则该自变量与其它的x变量完全独立；当vif(x_j)趋近于∞时，该自变量x_j与其它x变量有相当严重的多重共线性。一般当vif(x_j)≥10时，认为x_j与其它x变量有严重的多重共线性。

 最大条件指数记为f，当f>10时，且当该自变量的变异由每一个主成分解释所占比例vp>0.5时，可能认为这些自变量是严重相关的。

 如果自变量性存在共线性，根据偏相关系数大小，去掉其中一个对因变量影响最小的自变量，或根据方差比例vp的大小，去掉vp值大的自变量，再重新作共线性诊断，直至多重共线性不存在为止。

(2)残差的独立性

多元线性回归的残差独立性诊断等价于检查数据是否受趋势影响，可以绘制e*t散点图或e_i*e_i-1散点图；也可以用Durbin-Watson检验方法，计算DW值来判断随机误差项e_i是否一阶自相关，DW值的聚会范围在0~4之间，接近0或4，则可以认为具有一阶自相关。

如果残差间存在一阶自相关，则计算因变量的一阶差商，以此为新的因变量进行分析。这种情况通常多数出现在时间序列数据。

(3)残差的均值为零，方差为常数

 多元线性回归的自变量与残差的独立性可通过绘制残差和预测值的散点图来检验残差的均值和方差的齐性。如果残差随机地分布在横轴的上下两侧，形成一个很窄的条带状，则可以认为残差的均值为零，方差为常数。否则，说明残差的均值不为零，或残差的变异不均匀。

如果残差的均值不为零或方差不为常数，首先应用学生化残差Student或Cook的距离残差Cook’s D应检查数据中是否存在异常点。如果Student>或D>0.5，可考虑异常点的存在。如果数据中不存在异常点，可以用加权回归分析，消除方差的影响，或将因变量进行变量变换再拟合回归模型。

(4)残差服从正态分布

 多元线性回归模型残差的正态性可通过绘制残差的直方图和累积概率图来检验其正态性。如果不服从正态分布，可以对因变量进行变量变换，使得因变量近似地服从正态分布。

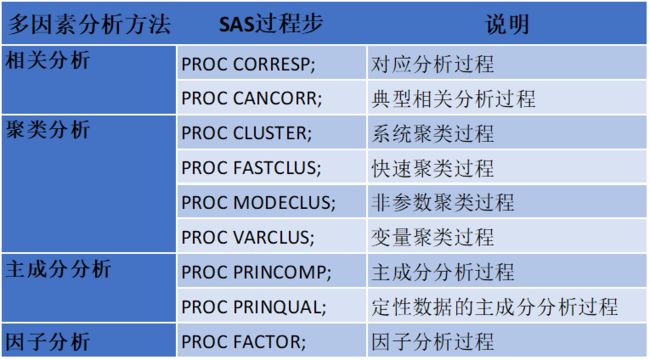
另：上期的表11-2有个小错误，在此作以纠正，向各位读者道歉！更正后的表如下：

表11-2 研究因素间互依性常用的统计学方法及其SAS过程步

  

       整理不易，欢迎点亮再看哦！

参考文献：

[1] 高惠璇. SAS系统SAS/STAT软件使用手册[M]. 北京：中国统计出版社, 1997.

[2] 孙振球, 徐勇勇. 医学统计学[M].北京：人民卫生出版社, 2014.

[3] 张家放. 医用多元统计方法[M]. 武汉：华中科技大学出版社, 2002.

SAS系列推文

【赠人玫瑰，手留余香】

----------------------------------------------

SAS系列32：SAS高级统计(一)

SAS系列31：SAS宏语言(四)

SAS系列30：SAS宏语言(三)

SAS系列29：SAS宏语言(二)

SAS系列28：SAS宏语言(一)

SAS系列27：线性回归

SAS系列26：双变量数据假设检验

SAS系列25：双向有序列联表检验

SAS系列24：单向有序列联表资料的假设检验

SAS系列23：列联表资料假设检验方法

SAS系列22：定性数据假设检验

SAS系列21：SAS统计推断(六)

SAS系列20：SAS统计推断(五)

SAS系列19：SAS统计推断(四)

SAS系列18：SAS统计推断(三)

SAS系列17：SAS统计推断(二)

SAS系列16：SAS统计推断(一)

SAS系列15：SAS数据可视化结果输出

SAS系列14：SAS数据可视化(三)

SAS系列13：SAS数据可视化(二)

SAS系列12：SAS数据可视化(一)

SAS系列11：SAS基础统计过程(三)

SAS系列10：SAS基础统计过程(二)

SAS系列09：SAS 基础统计计算过程

SAS系列08：SAS函数

SAS系列07：SAS数据整理(三)

SAS系列06：SAS数据整理(二)

SAS系列05：SAS数据整理(一)

SAS系列04：SAS数据导入

SAS系列03：SAS入门(二)之SAS编程语言基础

SAS系列02：SAS入门(一)

SAS系列01：统计分析航空母舰-SAS简介

----------------------------------------------

精鼎特邀