动手强化学习(七):DQN 改进算法——Double DQN
动手强化学习(七):DQN 改进算法——Double DQN
- 1. 简介
- 2. Double DQN
- 3. Double DQN代码实战
文章转于 伯禹学习平台-动手学强化学习 (强推)
本文所有代码均可在jupyter notebook运行
与君共勉,一起学习。
1. 简介
DQN 算法敲开了深度强化学习的大门,但是作为先驱性的工作,其本身存在着一些问题以及一些可以改进的地方。于是,在 DQN 之后,学术界涌现出了非常多的改进算法。本章将介绍其中两个非常著名的算法:Double DQN 和 Dueling DQN,这两个算法的实现非常简单,只需要在 DQN 的基础上稍加修改,它们能在一定程度上改善 DQN 的效果。
2. Double DQN
普通的 DQN 算法通常会导致对 Q Q Q 值的过高估计 (overestimation) 。传统 DQN 优化的 TD 误差目标为
r + γ max a ′ Q ω − ( s ′ , a ′ ) r+\gamma \max _{a^{\prime}} Q_{\omega^{-}}\left(s^{\prime}, a^{\prime}\right) r+γa′maxQω−(s′,a′)
其中 max a ′ Q ω − ( s ′ , a ′ ) \max _{a^{\prime}} Q_{\omega^{-}}\left(s^{\prime}, a^{\prime}\right) maxa′Qω−(s′,a′) 由目标网络(参数为 ω − \omega^{-} ω−) 计算得出,我们还可以将其写成如下形式:
Q ω − ( s ′ , arg max a ′ Q ω − ( s ′ , a ′ ) ) Q_{\omega^{-}}\left(s^{\prime}, \arg \max _{a^{\prime}} Q_{\omega^{-}}\left(s^{\prime}, a^{\prime}\right)\right) Qω−(s′,arga′maxQω−(s′,a′))
换句话说,max操作实际可以被拆解为两部分:首先选取状态 s ′ s^{\prime} s′ 下的最优动作 a ∗ = arg max a ′ Q ω − ( s ′ , a ′ ) a^{*}=\arg \max _{a^{\prime}} Q_{\omega^{-}}\left(s^{\prime}, a^{\prime}\right) a∗=argmaxa′Qω−(s′,a′) ,接着计算该动作对应的价值 Q ω − ( s ′ , a ∗ ) Q_{\omega^{-}}\left(s^{\prime}, a^{*}\right) Qω−(s′,a∗) 。当这两部分采用同一套 Q 网络进行计算 时,每次得到的都是神经网络当前估算的所有动作价值中的最大值。考虑到通过神经网络估算的 Q Q Q 值本身在某些时候会产生正向或负向的误差,在 DQN 的更新方式下神经网络会将正向误差累 积。例如,我们考虑一个特殊情形: 在状态 s ′ s^{\prime} s′ 下所有动作的 Q Q Q 值均为 0 ,即 Q ( s ′ , a i ) = 0 , ∀ i Q\left(s^{\prime}, a_{i}\right)=0, \forall i Q(s′,ai)=0,∀i ,此时正确的更新目标应为 r + 0 = r r+0=r r+0=r ,但是由于神经网络拟合的误差通常会出现某些动作的估算有正 误差的情况,即存在某个动作 a ′ a^{\prime} a′ 有 Q ( s ′ , a ′ ) > 0 Q\left(s^{\prime}, a^{\prime}\right)>0 Q(s′,a′)>0 ,此时我们的更新目标出现了过高估计, r + γ max Q > r + 0 r+\gamma \max Q>r+0 r+γmaxQ>r+0 。因此,当我们用 DQN 的更新公式进行更新时, Q ( s , a ) Q(s, a) Q(s,a) 也就会被过高估计了。同 理,我们拿这个 Q ( s , a ) Q(s, a) Q(s,a) 来作为更新目标来更新上一步的 Q Q Q 值时,同样会过高估计,这样的误差将会逐步累积。对于动作空间较大的任务, DQN 中的过高估计问题会非常严重,造成 DQN 无法有 效工作的后果。
为了解决这一问题,Double DQN 算法提出利用两个独立训练的神经网络估算 max a ′ Q ∗ ( s ′ , a ′ ) \max _{a^{\prime}} Q_{*}\left(s^{\prime}, a^{\prime}\right) maxa′Q∗(s′,a′) 。具体做法是将原有的 max a ′ Q ω − ( s ′ , a ′ ) \max _{a^{\prime}} Q_{\omega^{-}}\left(s^{\prime}, a^{\prime}\right) maxa′Qω−(s′,a′) 更改为 Q ω − ( s ′ , arg max a ′ Q ω ( s ′ , a ′ ) ) Q_{\omega^{-}}\left(s^{\prime}, \arg \max _{a^{\prime}} Q_{\omega}\left(s^{\prime}, a^{\prime}\right)\right) Qω−(s′,argmaxa′Qω(s′,a′)) ,即利用一套神经 网络 Q ω Q_{\omega} Qω 的输出选取价值最大的动作,但在使用该动作的价值时,用另一套神经网络 Q ω − Q_{\omega}^{-} Qω−计算该动作的价值。这样,即使其中一套神经网络的某个动作存在比较严重的过高估计问题,由于另一套神 经网络的存在,这个动作最终使用的 Q Q Q 值不会存在很大的过高估计问题。
在传统的 DQN 算法中,本来就存在两套 Q Q Q 函数的神经网络——目标网络和训练网络(参见 7.3.2 节),只不过 m a x a ′ Q ω − ( s ′ , a ′ ) \mathrm{max}_{a^{\prime}} Q_{\omega^{-}}\left(s^{\prime}, a^{\prime}\right) maxa′Qω−(s′,a′) 的计算只用到了其中的目标网络,那么我们恰好可以直接将训练 网络作为 Double DQN 算法中的第一套神经网络来选取动作,将目标网络作为第二套神经网络计算 Q Q Q 值,这便是 Double DQN 的主要思想。由于在 DQN 算法中将训练网络的参数记为 ω \omega ω ,将目标 网络的参数记为 ω − \omega^{-} ω−,这与本节中 Double DQN 的两套神经网络的参数是统一的,因此,我们可以直接写出如下 Double DQN 的优化目标:
r + γ Q ω − ( s ′ , arg max a ′ Q ω ( s ′ , a ′ ) ) r+\gamma Q_{\omega^{-}}\left(s^{\prime}, \underset{a^{\prime}}{\arg \max } Q_{\omega}\left(s^{\prime}, a^{\prime}\right)\right) r+γQω−(s′,a′argmaxQω(s′,a′))
3. Double DQN代码实战
显然, DQN 与 Double DQN 的差别只是在于计算状态 s ′ s^{\prime} s′ 下 Q Q Q 值时如何选取动作:
- DQN 的优化目标可以写为 r + γ Q ω − ( s ′ , arg max a ′ Q ω − ( s ′ , a ′ ) ) r+\gamma Q_{\omega^{-}}\left(s^{\prime}, \arg \max _{a^{\prime}} Q_{\omega^{-}}\left(s^{\prime}, a^{\prime}\right)\right) r+γQω−(s′,argmaxa′Qω−(s′,a′)) ,动作的选取依靠目标网络 Q ω − Q_{\omega^{-}} Qω−;
- Double DQN 的优化目标为 r + γ Q ω − ( s ′ , arg max a ′ Q ω ( s ′ , a ′ ) ) r+\gamma Q_{\omega^{-}}\left(s^{\prime}, \arg \max _{a^{\prime}} Q_{\omega}\left(s^{\prime}, a^{\prime}\right)\right) r+γQω−(s′,argmaxa′Qω(s′,a′)) , 动作的选取依靠训练网络 Q ω 0 Q_{\omega_{0}} Qω0 。
所以 Double DQN 的代码实现可以直接在 DQN 的基础上进行,无须做过多修改。
本节采用的环境是倒立摆(Inverted Pendulum),该环境下有一个处于随机位置的倒立摆,如图 8-1 所示。环境的状态包括倒立摆角度的正弦值 s i n θ s i n \theta sinθ ,余弦值cos θ \theta θ ,角速度 θ ; \theta_{\text {; }} θ; ;动作为对倒立摆施 加的力矩,详情参见表 8-1 和表 8-2。每一步都会根据当前倒立摆的状态的好坏给予智能体不同的奖励,该环境的奖励函数为 − ( θ 2 + 0.1 θ ˙ 2 + 0.001 a 2 ) -\left(\theta^{2}+0.1 \dot{\theta}^{2}+0.001 a^{2}\right) −(θ2+0.1θ˙2+0.001a2) ,倒立摆向上保持直立不动时奖励为 0 , 倒立摆在其他位置时奖励为负数。环境本身没有终止状态,运行 200 步后游戏自动结束。

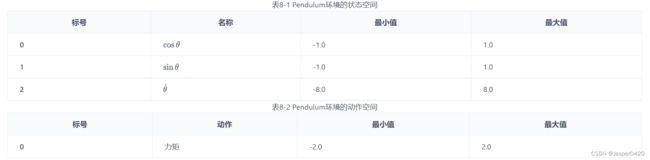
力矩大小是在 [ − 2 , 2 ] [-2,2] [−2,2]范围内的连续值。由于 DQN 只能处理离散动作环境,因此我们无法直接用 DQN 来处理倒立摆环境,但倒立摆环境可以比较方便地验证 DQN 对值 Q Q Q的过高估计:倒立摆环境下 Q Q Q值的最大估计应为 0(倒立摆向上保持直立时能选取的最大 Q Q Q值), Q Q Q值出现大于 0 的情况则说明出现了过高估计。为了能够应用 DQN,我们采用离散化动作的技巧。例如,下面的代码将连续的动作空间离散为 11 个动作。动作 [ 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 ] [0,1,2,3,4,5,6,7,8,9,10] [0,1,2,3,4,5,6,7,8,9,10]分别代表力矩为 [ − 2 , − 1.6 , − 1.2 , . . . . 1.2 , 1.6 , 2 ] [-2,-1.6,-1.2,....1.2,1.6,2] [−2,−1.6,−1.2,....1.2,1.6,2]。
import random
import gym
import numpy as np
import torch
import torch.nn.functional as F
import matplotlib.pyplot as plt
import rl_utils
from tqdm import tqdm
class Qnet(torch.nn.Module):
''' 只有一层隐藏层的Q网络 '''
def __init__(self, state_dim, hidden_dim, action_dim):
super(Qnet, self).__init__()
self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
self.fc2 = torch.nn.Linear(hidden_dim, action_dim)
def forward(self, x):
x = F.relu(self.fc1(x))
return self.fc2(x)
接下来我们在 DQN 代码的基础上稍做修改以实现 Double DQN。
class DQN:
''' DQN算法,包括Double DQN '''
def __init__(self,
state_dim,
hidden_dim,
action_dim,
learning_rate,
gamma,
epsilon,
target_update,
device,
dqn_type='VanillaDQN'):
self.action_dim = action_dim
self.q_net = Qnet(state_dim, hidden_dim, self.action_dim).to(device)
self.target_q_net = Qnet(state_dim, hidden_dim,
self.action_dim).to(device)
self.optimizer = torch.optim.Adam(self.q_net.parameters(),
lr=learning_rate)
self.gamma = gamma
self.epsilon = epsilon
self.target_update = target_update
self.count = 0
self.dqn_type = dqn_type
self.device = device
def take_action(self, state):
if np.random.random() < self.epsilon:
action = np.random.randint(self.action_dim)
else:
state = torch.tensor([state], dtype=torch.float).to(self.device)
action = self.q_net(state).argmax().item()
return action
def max_q_value(self, state):
state = torch.tensor([state], dtype=torch.float).to(self.device)
return self.q_net(state).max().item()
def update(self, transition_dict):
states = torch.tensor(transition_dict['states'],
dtype=torch.float).to(self.device)
actions = torch.tensor(transition_dict['actions']).view(-1, 1).to(
self.device)
rewards = torch.tensor(transition_dict['rewards'],
dtype=torch.float).view(-1, 1).to(self.device)
next_states = torch.tensor(transition_dict['next_states'],
dtype=torch.float).to(self.device)
dones = torch.tensor(transition_dict['dones'],
dtype=torch.float).view(-1, 1).to(self.device)
q_values = self.q_net(states).gather(1, actions) # Q值
# 下个状态的最大Q值
if self.dqn_type == 'DoubleDQN': # DQN与Double DQN的区别
max_action = self.q_net(next_states).max(1)[1].view(-1, 1)
max_next_q_values = self.target_q_net(next_states).gather(1, max_action)
else: # DQN的情况
max_next_q_values = self.target_q_net(next_states).max(1)[0].view(-1, 1)
q_targets = rewards + self.gamma * max_next_q_values * (1 - dones) # TD误差目标
dqn_loss = torch.mean(F.mse_loss(q_values, q_targets)) # 均方误差损失函数
self.optimizer.zero_grad() # PyTorch中默认梯度会累积,这里需要显式将梯度置为0
dqn_loss.backward() # 反向传播更新参数
self.optimizer.step()
if self.count % self.target_update == 0:
self.target_q_net.load_state_dict(
self.q_net.state_dict()) # 更新目标网络
self.count += 1
接下来我们设置相应的超参数,并实现将倒立摆环境中的连续动作转化为离散动作的函数。
lr = 1e-2
num_episodes = 200
hidden_dim = 128
gamma = 0.98
epsilon = 0.01
target_update = 50
buffer_size = 5000
minimal_size = 1000
batch_size = 64
device = torch.device("cuda") if torch.cuda.is_available() else torch.device(
"cpu")
env_name = 'Pendulum-v0'
env = gym.make(env_name)
state_dim = env.observation_space.shape[0]
action_dim = 11 # 将连续动作分成11个离散动作
def dis_to_con(discrete_action, env, action_dim): # 离散动作转回连续的函数
action_lowbound = env.action_space.low[0] # 连续动作的最小值
action_upbound = env.action_space.high[0] # 连续动作的最大值
return action_lowbound + (discrete_action /
(action_dim - 1)) * (action_upbound -
action_lowbound)
接下来要对比 DQN 和 Double DQN 的训练情况,为了便于后续多次调用,我们进一步将 DQN 算法的训练过程定义成一个函数。训练过程会记录下每个状态的最大 Q Q Q值,在训练完成后我们可以将结果可视化,观测这些 Q Q Q值存在的过高估计的情况,以此来对比 DQN 和 Double DQN 的不同。
def train_DQN(agent, env, num_episodes, replay_buffer, minimal_size,
batch_size):
return_list = []
max_q_value_list = []
max_q_value = 0
for i in range(10):
with tqdm(total=int(num_episodes / 10),
desc='Iteration %d' % i) as pbar:
for i_episode in range(int(num_episodes / 10)):
episode_return = 0
state = env.reset()
done = False
while not done:
action = agent.take_action(state)
max_q_value = agent.max_q_value(
state) * 0.005 + max_q_value * 0.995 # 平滑处理
max_q_value_list.append(max_q_value) # 保存每个状态的最大Q值
action_continuous = dis_to_con(action, env,
agent.action_dim)
next_state, reward, done, _ = env.step([action_continuous])
replay_buffer.add(state, action, reward, next_state, done)
state = next_state
episode_return += reward
if replay_buffer.size() > minimal_size:
b_s, b_a, b_r, b_ns, b_d = replay_buffer.sample(
batch_size)
transition_dict = {
'states': b_s,
'actions': b_a,
'next_states': b_ns,
'rewards': b_r,
'dones': b_d
}
agent.update(transition_dict)
return_list.append(episode_return)
if (i_episode + 1) % 10 == 0:
pbar.set_postfix({
'episode':
'%d' % (num_episodes / 10 * i + i_episode + 1),
'return':
'%.3f' % np.mean(return_list[-10:])
})
pbar.update(1)
return return_list, max_q_value_list
一切就绪!我们首先训练 DQN 并打印出其学习过程中最大 Q Q Q值的情况。
random.seed(0)
np.random.seed(0)
env.seed(0)
torch.manual_seed(0)
replay_buffer = rl_utils.ReplayBuffer(buffer_size)
agent = DQN(state_dim, hidden_dim, action_dim, lr, gamma, epsilon,
target_update, device)
return_list, max_q_value_list = train_DQN(agent, env, num_episodes,
replay_buffer, minimal_size,
batch_size)
episodes_list = list(range(len(return_list)))
mv_return = rl_utils.moving_average(return_list, 5)
plt.plot(episodes_list, mv_return)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('DQN on {}'.format(env_name))
plt.show()
frames_list = list(range(len(max_q_value_list)))
plt.plot(frames_list, max_q_value_list)
plt.axhline(0, c='orange', ls='--')
plt.axhline(10, c='red', ls='--')
plt.xlabel('Frames')
plt.ylabel('Q value')
plt.title('DQN on {}'.format(env_name))
plt.show()
-----------------------------------------------------------------------------------------
Iteration 0: 100%|██████████| 20/20 [00:02<00:00, 7.14it/s, episode=20, return=-1018.764]
Iteration 1: 100%|██████████| 20/20 [00:03<00:00, 5.73it/s, episode=40, return=-463.311]
Iteration 2: 100%|██████████| 20/20 [00:03<00:00, 5.53it/s, episode=60, return=-184.817]
Iteration 3: 100%|██████████| 20/20 [00:03<00:00, 5.55it/s, episode=80, return=-317.366]
Iteration 4: 100%|██████████| 20/20 [00:03<00:00, 5.67it/s, episode=100, return=-208.929]
Iteration 5: 100%|██████████| 20/20 [00:03<00:00, 5.59it/s, episode=120, return=-182.659]
Iteration 6: 100%|██████████| 20/20 [00:03<00:00, 5.25it/s, episode=140, return=-275.938]
Iteration 7: 100%|██████████| 20/20 [00:03<00:00, 5.65it/s, episode=160, return=-209.702]
Iteration 8: 100%|██████████| 20/20 [00:03<00:00, 5.73it/s, episode=180, return=-246.861]
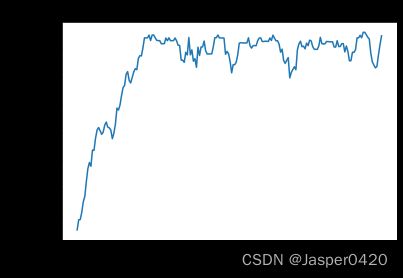

根据代码运行结果我们可以发现,DQN 算法在倒立摆环境中能取得不错的回报,最后的期望回报在-200 左右,但是不少 Q Q Q值超过了 0,有一些还超过了 10,该现象便是 DQN 算法中的 Q Q Q值过高估计。我们现在来看一下 Double DQN 是否能对此问题进行改善。
random.seed(0)
np.random.seed(0)
env.seed(0)
torch.manual_seed(0)
replay_buffer = rl_utils.ReplayBuffer(buffer_size)
agent = DQN(state_dim, hidden_dim, action_dim, lr, gamma, epsilon,
target_update, device, 'DoubleDQN')
return_list, max_q_value_list = train_DQN(agent, env, num_episodes,
replay_buffer, minimal_size,
batch_size)
episodes_list = list(range(len(return_list)))
mv_return = rl_utils.moving_average(return_list, 5)
plt.plot(episodes_list, mv_return)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('Double DQN on {}'.format(env_name))
plt.show()
frames_list = list(range(len(max_q_value_list)))
plt.plot(frames_list, max_q_value_list)
plt.axhline(0, c='orange', ls='--')
plt.axhline(10, c='red', ls='--')
plt.xlabel('Frames')
plt.ylabel('Q value')
plt.title('Double DQN on {}'.format(env_name))
plt.show()
-----------------------------------------------------------------------------------------------------
Iteration 0: 100%|██████████| 20/20 [00:03<00:00, 6.60it/s, episode=20, return=-818.719]
Iteration 1: 100%|██████████| 20/20 [00:03<00:00, 5.43it/s, episode=40, return=-391.392]
Iteration 2: 100%|██████████| 20/20 [00:03<00:00, 5.29it/s, episode=60, return=-216.078]
Iteration 3: 100%|██████████| 20/20 [00:03<00:00, 5.52it/s, episode=80, return=-438.220]
Iteration 4: 100%|██████████| 20/20 [00:03<00:00, 5.42it/s, episode=100, return=-162.128]
Iteration 5: 100%|██████████| 20/20 [00:03<00:00, 5.50it/s, episode=120, return=-389.088]
Iteration 6: 100%|██████████| 20/20 [00:03<00:00, 5.44it/s, episode=140, return=-273.700]
Iteration 7: 100%|██████████| 20/20 [00:03<00:00, 5.23it/s, episode=160, return=-221.605]
Iteration 8: 100%|██████████| 20/20 [00:04<00:00, 4.91it/s, episode=180, return=-262.134]
Iteration 9: 100%|██████████| 20/20 [00:03<00:00, 5.34it/s, episode=200, return=-278.752]
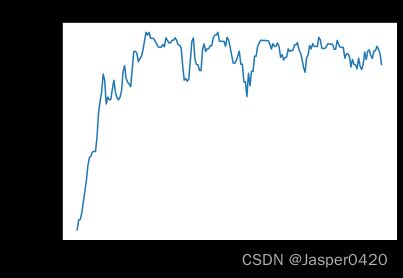
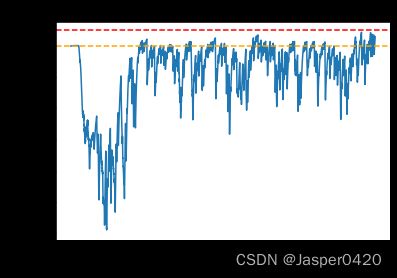
我们可以发现,与普通的 DQN 相比,Double DQN 比较少出现 Q Q Q值大于 0 的情况,说明 Q Q Q值过高估计的问题得到了很大缓解。
相关资源来自:伯禹学习平台-动手学强化学习
![]()