机器学习强化(决策树和随机森林)
一、鸢尾花数据的决策树分类及树深度与过拟合关系
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib as mpl
from sklearn import tree
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn.pipeline import Pipeline
import pydotplus
# 花萼长度、花萼宽度,花瓣长度,花瓣宽度
iris_feature_E = 'sepal length', 'sepal width', 'petal length', 'petal width'
iris_feature = u'花萼长度', u'花萼宽度', u'花瓣长度', u'花瓣宽度'
iris_class = 'Iris-setosa', 'Iris-versicolor', 'Iris-virginica'
if __name__ == "__main__":
mpl.rcParams['font.sans-serif'] = [u'SimHei']
mpl.rcParams['axes.unicode_minus'] = False
data = pd.read_csv('iris.data', header=None)
# 重新设置列名称、属性
columns = ['sepal_length', 'sepal_width', 'petal_length', 'petal_width', 'type']
data.rename(columns=dict(zip(np.arange(5), columns)), inplace=True)
data['type'] = pd.Categorical(data['type']).codes
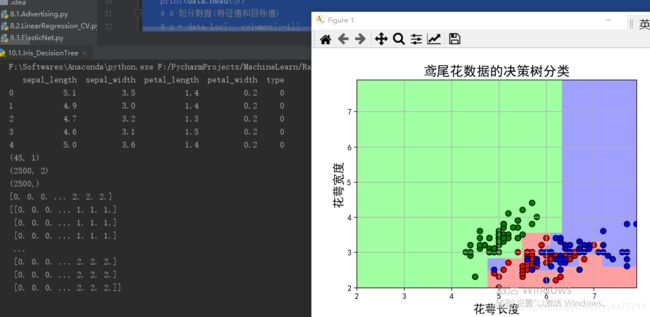
print(data.head(5))
# # 划分数据(特征值和目标值)
# x = data.loc[:, columns[:-1]]
# y = data['type']
x, y = np.split(data.values, (4,), axis=1)
# print 'x = \n', x
# print 'y = \n', y
# 仅使用前两列特征
x = x[:, :2]
# path = 'iris.data' # 数据文件路径
# data = pd.read_csv(path, header=None)
# x = data[range(4)]
# y = pd.Categorical(data[4]).codes
# # 为了可视化,仅使用前两列特征
#x = x.iloc[:, :2]
x_train, x_test, y_train, y_test = train_test_split(x, y, train_size=0.7, random_state=1)
print (y_test.shape)
# 决策树参数估计
# min_samples_split = 10:如果该结点包含的样本数目大于10,则(有可能)对其分支
# min_samples_leaf = 10:若将某结点分支后,得到的每个子结点样本数目都大于10,则完成分支;否则,不进行分支
model = DecisionTreeClassifier(criterion='gini')
model.fit(x_train, y_train)
y_test_hat = model.predict(x_test) # 测试数据
# 保存
# dot -Tpng my.dot -o my.png
# 1、输出
# with open('iris.dot', 'w') as f:
# tree.export_graphviz(model, out_file=f)
# 2、给定文件名
# tree.export_graphviz(model, out_file='iris1.dot')
# 3、输出为pdf格式
# dot_data = tree.export_graphviz(model, out_file=None, feature_names=iris_feature_E, class_names=iris_class,
# filled=True, rounded=True, special_characters=True)
# graph = pydotplus.graph_from_dot_data(dot_data)
# #graph.write_pdf('iris.pdf')
# f = open('iris.png', 'wb')
# f.write(graph.create_png())
# f.close()
# 画图
N, M = 50, 50 # 横纵各采样多少个值
x1_min, x2_min = x.min(),x.min()
x1_max, x2_max = x.max(),x.max()
t1 = np.linspace(x1_min, x1_max, N)
t2 = np.linspace(x2_min, x2_max, M)
x1, x2 = np.meshgrid(t1, t2) # 生成网格采样点
x_show = np.stack((x1.flat, x2.flat), axis=1) # 测试点
print (x_show.shape)
# # 无意义,只是为了凑另外两个维度
# # 打开该注释前,确保注释掉x = x[:, :2]
# x3 = np.ones(x1.size) * np.average(x[:, 2])
# x4 = np.ones(x1.size) * np.average(x[:, 3])
# x_test = np.stack((x1.flat, x2.flat, x3, x4), axis=1) # 测试点
cm_light = mpl.colors.ListedColormap(['#A0FFA0', '#FFA0A0', '#A0A0FF'])
cm_dark = mpl.colors.ListedColormap(['g', 'r', 'b'])
y_show_hat = model.predict(x_show) # 预测值
print (y_show_hat.shape)
print (y_show_hat)
y_show_hat = y_show_hat.reshape(x1.shape) # 使之与输入的形状相同
print (y_show_hat)
plt.figure(facecolor='w')
plt.pcolormesh(x1, x2, y_show_hat, cmap=cm_light) # 预测值的显示
# #plt.scatter(x_test[0], x_test[1], y_show_hat, edgecolors='k', s=150, cmap=cm_dark, marker='*') # 测试数据
#plt.scatter(x[0], x[1], c=y.ravel(), s=40, cmap=cm_dark) # 全部数据
plt.scatter(x[:, 0], x[:, 1], c=np.squeeze(y), edgecolors='k', s=50, cmap=cm_dark) # 样本的显示
plt.xlabel(iris_feature[0], fontsize=15)
plt.ylabel(iris_feature[1], fontsize=15)
plt.xlim(x1_min, x1_max)
plt.ylim(x2_min, x2_max)
plt.grid(True)
plt.title(u'鸢尾花数据的决策树分类', fontsize=17)
plt.show()
# 训练集上的预测结果
y_test = y_test.reshape(-1)
print (y_test_hat)
print (y_test)
result = (y_test_hat == y_test) # True则预测正确,False则预测错误
acc = np.mean(result)
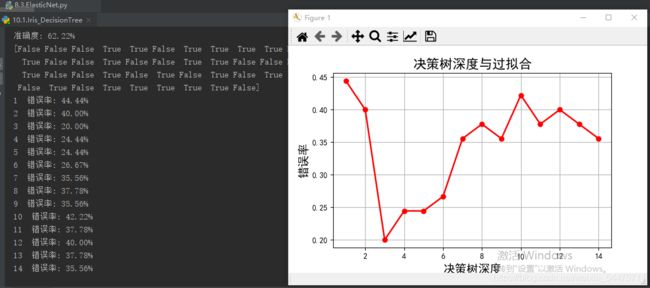
print ('准确度: %.2f%%' % (100 * acc))
# 过拟合:错误率
depth = np.arange(1, 15)
err_list = []
for d in depth:
clf = DecisionTreeClassifier(criterion='entropy', max_depth=d)
clf.fit(x_train, y_train)
y_test_hat = clf.predict(x_test) # 测试数据
result = (y_test_hat == y_test) # True则预测正确,False则预测错误
if d == 1:
print (result)
err = 1 - np.mean(result)
err_list.append(err)
# print d, ' 准确度: %.2f%%' % (100 * err)
print (d, ' 错误率: %.2f%%' % (100 * err))
plt.figure(facecolor='w')
plt.plot(depth, err_list, 'ro-', lw=2)
plt.xlabel(u'决策树深度', fontsize=15)
plt.ylabel(u'错误率', fontsize=15)
plt.title(u'决策树深度与过拟合', fontsize=17)
plt.grid(True)
plt.show()
import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeClassifier
# 'sepal length', 'sepal width', 'petal length', 'petal width'
iris_feature = u'花萼长度', u'花萼宽度', u'花瓣长度', u'花瓣宽度'
if __name__ == "__main__":
mpl.rcParams['font.sans-serif'] = [u'SimHei'] # 黑体 FangSong/KaiTi
mpl.rcParams['axes.unicode_minus'] = False
data = pd.read_csv('iris.data', header=None)
# # 重新设置列名称、属性
# columns = ['sepal_length', 'sepal_width', 'petal_length', 'petal_width', 'type']
# data.rename(columns=dict(zip(np.arange(5), columns)), inplace=True)
# data['type'] = pd.Categorical(data['type']).codes
# print(data.head(5))
# # # 划分数据(特征值和目标值)
# # x = data.loc[:, columns[:-1]]
# # y = data['type']
#
# x, y = np.split(data.values, (4,), axis=1)
# path = '..\\8.Regression\\iris.data' # 数据文件路径
# data = pd.read_csv(path, header=None)
x_prime = data[range(4)]
y = pd.Categorical(data[4]).codes
feature_pairs = [[0, 1], [0, 2], [0, 3], [1, 2], [1, 3], [2, 3]]
plt.figure(figsize=(10, 9), facecolor='#FFFFFF')
for i, pair in enumerate(feature_pairs):
# 准备数据
x = x_prime[pair]
# 决策树学习
clf = DecisionTreeClassifier(criterion='entropy', min_samples_leaf=3)
clf.fit(x, y)
# 画图
N, M = 500, 500 # 横纵各采样多少个值
x1_min, x2_min = x.min()
x1_max, x2_max = x.max()
t1 = np.linspace(x1_min, x1_max, N)
t2 = np.linspace(x2_min, x2_max, M)
x1, x2 = np.meshgrid(t1, t2) # 生成网格采样点
x_test = np.stack((x1.flat, x2.flat), axis=1) # 测试点
# 训练集上的预测结果
y_hat = clf.predict(x)
y = y.reshape(-1)
c = np.count_nonzero(y_hat == y) # 统计预测正确的个数
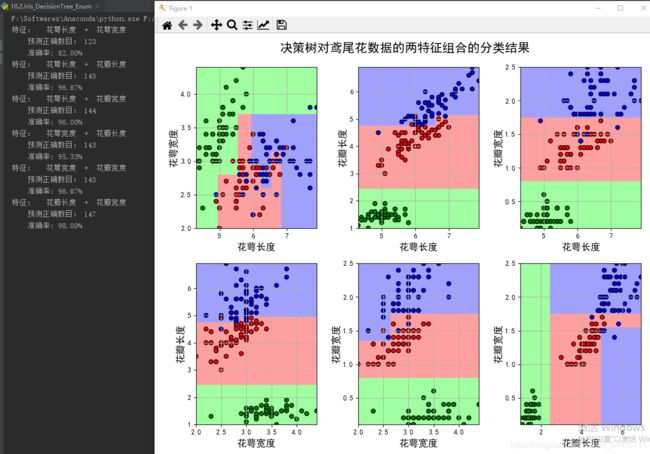
print ('特征: ', iris_feature[pair[0]], ' + ', iris_feature[pair[1]],)
print ('\t预测正确数目:', c,)
print ('\t准确率: %.2f%%' % (100 * float(c) / float(len(y))))
# 显示
cm_light = mpl.colors.ListedColormap(['#A0FFA0', '#FFA0A0', '#A0A0FF'])
cm_dark = mpl.colors.ListedColormap(['g', 'r', 'b'])
y_hat = clf.predict(x_test) # 预测值
y_hat = y_hat.reshape(x1.shape) # 使之与输入的形状相同
plt.subplot(2, 3, i+1)
plt.pcolormesh(x1, x2, y_hat, cmap=cm_light) # 预测值
plt.scatter(x[pair[0]], x[pair[1]], c=y, edgecolors='k', cmap=cm_dark) # 样本
plt.xlabel(iris_feature[pair[0]], fontsize=14)
plt.ylabel(iris_feature[pair[1]], fontsize=14)
plt.xlim(x1_min, x1_max)
plt.ylim(x2_min, x2_max)
plt.grid()
plt.suptitle(u'决策树对鸢尾花数据的两特征组合的分类结果', fontsize=18)
plt.tight_layout(2)
plt.subplots_adjust(top=0.92)
plt.show()
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib as mpl
from sklearn.ensemble import RandomForestClassifier
def iris_type(s):
it = {'Iris-setosa': 0, 'Iris-versicolor': 1, 'Iris-virginica': 2}
return it[s]
# 'sepal length', 'sepal width', 'petal length', 'petal width'
iris_feature = u'花萼长度', u'花萼宽度', u'花瓣长度', u'花瓣宽度'
if __name__ == "__main__":
mpl.rcParams['font.sans-serif'] = [u'SimHei'] # 黑体 FangSong/KaiTi
mpl.rcParams['axes.unicode_minus'] = False
# path = '..\\8.Regression\\iris.data' # 数据文件路径
# data = pd.read_csv(path, header=None)
data = pd.read_csv('iris.data', header=None)
x_prime = data[range(4)]
y = pd.Categorical(data[4]).codes
feature_pairs = [[0, 1], [0, 2], [0, 3], [1, 2], [1, 3], [2, 3]]
plt.figure(figsize=(10, 9), facecolor='#FFFFFF')
for i, pair in enumerate(feature_pairs):
# 准备数据
x = x_prime[pair]
# 随机森林
clf = RandomForestClassifier(n_estimators=200, criterion='entropy', max_depth=8)
clf.fit(x, y.ravel())
# 画图
N, M = 50, 50 # 横纵各采样多少个值
x1_min, x2_min = x.min()
x1_max, x2_max = x.max()
t1 = np.linspace(x1_min, x1_max, N)
t2 = np.linspace(x2_min, x2_max, M)
x1, x2 = np.meshgrid(t1, t2) # 生成网格采样点
x_test = np.stack((x1.flat, x2.flat), axis=1) # 测试点
# 训练集上的预测结果
y_hat = clf.predict(x)
y = y.reshape(-1)
c = np.count_nonzero(y_hat == y) # 统计预测正确的个数
print ('特征: ', iris_feature[pair[0]], ' + ', iris_feature[pair[1]],)
print ('\t预测正确数目:', c,)
print ('\t准确率: %.2f%%' % (100 * float(c) / float(len(y))))
# 显示
cm_light = mpl.colors.ListedColormap(['#A0FFA0', '#FFA0A0', '#A0A0FF'])
cm_dark = mpl.colors.ListedColormap(['g', 'r', 'b'])
y_hat = clf.predict(x_test) # 预测值
y_hat = y_hat.reshape(x1.shape) # 使之与输入的形状相同
plt.subplot(2, 3, i+1)
plt.pcolormesh(x1, x2, y_hat, cmap=cm_light) # 预测值
plt.scatter(x[pair[0]], x[pair[1]], c=y, edgecolors='k', cmap=cm_dark) # 样本
plt.xlabel(iris_feature[pair[0]], fontsize=14)
plt.ylabel(iris_feature[pair[1]], fontsize=14)
plt.xlim(x1_min, x1_max)
plt.ylim(x2_min, x2_max)
plt.grid()
plt.tight_layout(2.5)
plt.subplots_adjust(top=0.92)
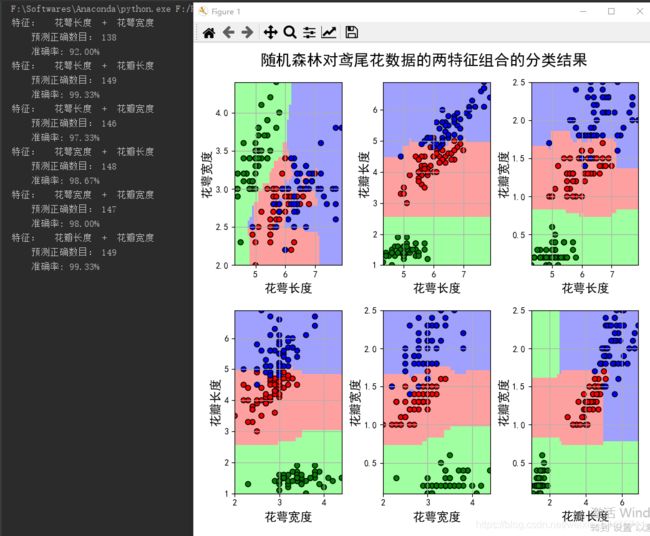
plt.suptitle(u'随机森林对鸢尾花数据的两特征组合的分类结果', fontsize=18)
plt.show()
四、Bagging
定义:从样本中重采样(有放回)选出n个样本
在所有属性上,对这n个样本建立分类器(ID3、C4.5、CART、SVM、Logistic回归等)
重复以上两步m次,即获得了m个分类器
将数据放在这m个分类器上,最后根据这m个分类器的投票结果,决定数据属于哪一类。
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
from sklearn.linear_model import RidgeCV
from sklearn.ensemble import BaggingRegressor
from sklearn.tree import DecisionTreeRegressor
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
def f(x):
return 0.5*np.exp(-(x+3) **2) + np.exp(-x**2) + 0.5*np.exp(-(x-3) ** 2)
if __name__ == "__main__":
np.random.seed(0)
N = 200
x = np.random.rand(N) * 10 - 5 # [-5,5)
x = np.sort(x)
y = f(x) + 0.05*np.random.randn(N)
x.shape = -1, 1
degree = 6
ridge = RidgeCV(alphas=np.logspace(-3, 2, 20), fit_intercept=False)
ridged = Pipeline([('poly', PolynomialFeatures(degree=degree)), ('Ridge', ridge)])
bagging_ridged = BaggingRegressor(ridged, n_estimators=100, max_samples=0.2)
dtr = DecisionTreeRegressor(max_depth=5)
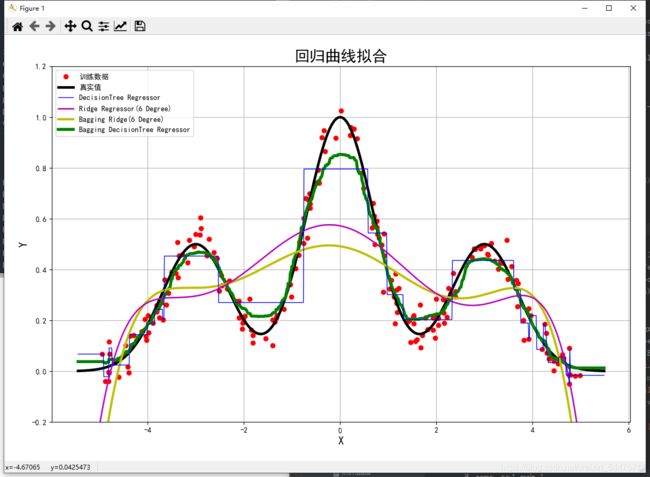
regs = [
('DecisionTree Regressor', dtr),
('Ridge Regressor(%d Degree)' % degree, ridged),
('Bagging Ridge(%d Degree)' % degree, bagging_ridged),
('Bagging DecisionTree Regressor', BaggingRegressor(dtr, n_estimators=100, max_samples=0.2))]
x_test = np.linspace(1.1*x.min(), 1.1*x.max(), 1000)
mpl.rcParams['font.sans-serif'] = [u'SimHei']
mpl.rcParams['axes.unicode_minus'] = False
plt.figure(figsize=(12, 8), facecolor='w')
plt.plot(x, y, 'ro', label=u'训练数据')
plt.plot(x_test, f(x_test), color='k', lw=3.5, label=u'真实值')
clrs = 'bmyg'
for i, (name, reg) in enumerate(regs):
reg.fit(x, y)
y_test = reg.predict(x_test.reshape(-1, 1))
plt.plot(x_test, y_test.ravel(), color=clrs[i], lw=i+1, label=name, zorder=6-i)
plt.legend(loc='upper left')
plt.xlabel('X', fontsize=15)
plt.ylabel('Y', fontsize=15)
plt.title(u'回归曲线拟合', fontsize=21)
plt.ylim((-0.2, 1.2))
plt.tight_layout(2)
plt.grid(True)
plt.show()
import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeRegressor
if __name__ == "__main__":
N = 100
x = np.random.rand(N) * 6 - 3 # [-3,3)
x.sort()
y = np.sin(x) + np.random.randn(N) * 0.05
print (y)
x = x.reshape(-1, 1) # 转置后,得到N个样本,每个样本都是1维的
print (x)
dt = DecisionTreeRegressor(criterion='mse', max_depth=9)
dt.fit(x, y)
x_test = np.linspace(-3, 3, 50).reshape(-1, 1)
y_hat = dt.predict(x_test)
plt.plot(x, y, 'r*', ms=10, label='Actual')
plt.plot(x_test, y_hat, 'g-', linewidth=2, label='Predict')
plt.legend(loc='upper left')
plt.grid()
plt.show()
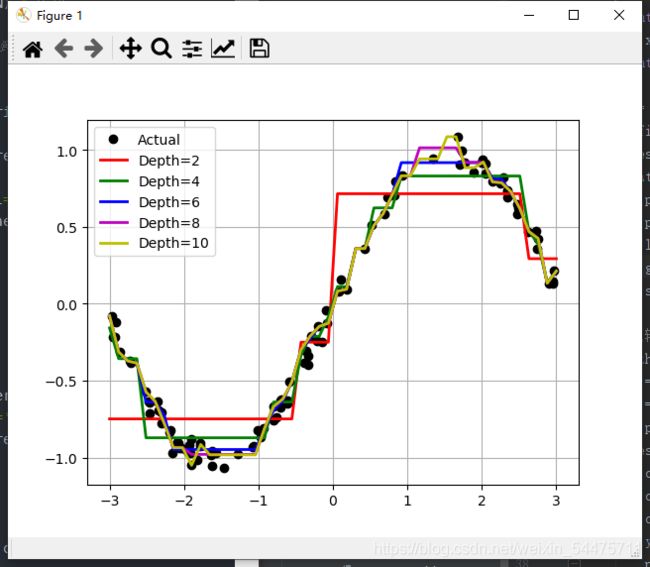
# 比较决策树的深度影响
depth = [2, 4, 6, 8, 10]
clr = 'rgbmy'
dtr = DecisionTreeRegressor(criterion='mse')
plt.plot(x, y, 'ko', ms=6, label='Actual')
x_test = np.linspace(-3, 3, 50).reshape(-1, 1)
for d, c in zip(depth, clr):
dtr.set_params(max_depth=d)
dtr.fit(x, y)
y_hat = dtr.predict(x_test)
plt.plot(x_test, y_hat, '-', color=c, linewidth=2, label='Depth=%d' % d)
plt.legend(loc='upper left')
plt.grid(b=True)
plt.show()
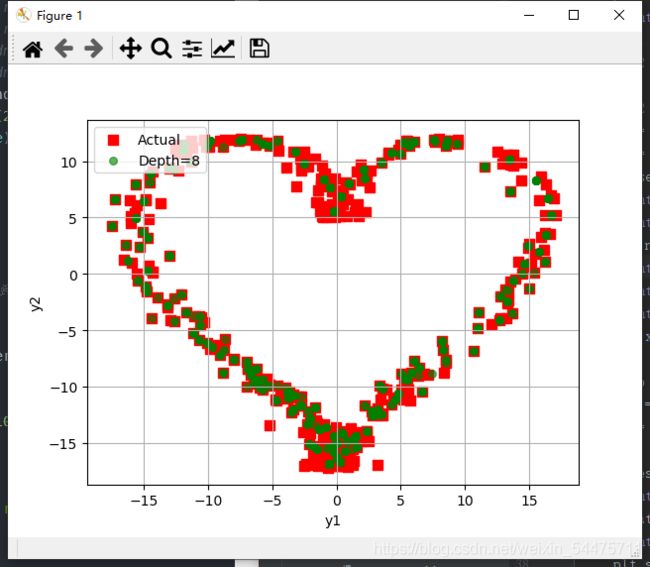
六、多输出的决策树回归
定义:以多个输出(下例为两个)作为轴建立图像,查看预测值与实际值的差别不大;
import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeRegressor
if __name__ == "__main__":
N = 400
x = np.random.rand(N) * 8 - 4 # [-4,4)
x.sort()
print (x)
print ('====================')
# y1 = np.sin(x) + 3 + np.random.randn(N) * 0.1
# y2 = np.cos(0.3*x) + np.random.randn(N) * 0.01
# y1 = np.sin(x) + np.random.randn(N) * 0.05
# y2 = np.cos(x) + np.random.randn(N) * 0.1
y1 = 16 * np.sin(x) ** 3 + np.random.randn(N)
y2 = 13 * np.cos(x) - 5 * np.cos(2*x) - 2 * np.cos(3*x) - np.cos(4*x) + 0.1* np.random.randn(N)
np.set_printoptions(suppress=True)
print (y1)
print (y2)
y = np.vstack((y1, y2)).T
print (y)
print ('Data = \n', np.vstack((x, y1, y2)).T)
print ('=================')
x = x.reshape(-1, 1) # 转置后,得到N个样本,每个样本都是1维的
deep = 8
reg = DecisionTreeRegressor(criterion='mse', max_depth=deep)
dt = reg.fit(x, y)
x_test = np.linspace(-4, 4, num=1000).reshape(-1, 1)
print (x_test)
y_hat = dt.predict(x_test)
print (y_hat)
plt.scatter(y[:, 0], y[:, 1], c='r', marker='s', s=60, label='Actual')
plt.scatter(y_hat[:, 0], y_hat[:, 1], c='g', marker='o', edgecolors='g', s=30, label='Depth=%d' % deep, alpha=0.6)
plt.legend(loc='upper left')
plt.xlabel('y1')
plt.ylabel('y2')
plt.grid()
plt.show()