python写二分法_Python实现二分法和黄金分割法
运筹学课上,首先介绍了非线性规划算法中的无约束规划算法。二分法和黄金分割法是属于无约束规划算法的一维搜索法中的代表。
二分法:$$x_{1}^{(k+1)}=\frac{1}{2}(x_{R}^{(k)}+x_{L}^{(k)}-\Delta)$$$$x_{2}^{(k+1)}=\frac{1}{2}(x_{R}^{(k)}+x_{L}^{(k)}+\Delta)$$
黄金分割法:$$x_{1}^{(k+1)}=x_{R}^{(k)}-(\frac{\sqrt{5}-1}{2})(x_{R}^{(k)}-x_{L}^{(k)})$$$$x_{2}^{(k+1)}=x_{L}^{(k)}+(\frac{\sqrt{5}-1}{2})(x_{R}^{(k)}-x_{L}^{(k)})$$
选择的$x_{1}^{(k+1)}$和$x_{2}^{(k+1)}$一定满足$$x_{L}^{(k)}
下面确定新的不确定空间$I^{(k+1)}$
情况1:若$f(x_{1}^{(k+1)})>f(x_{2}^{(k+1)})$,则$I^{(k+1)}=\left[x_{L}^{(k)},x_{2}^{(k+1)}\right]$
情况2:若$f(x_{1}^{(k+1)})
情况3:若$f(x_{1}^{(k+1)})=f(x_{2}^{(k+1)})$,则$I^{(k+1)}=\left[x_{1}^{(k+1)},x_{2}^{(k+1)}\right]$
下面记录下用Python实现二分法和黄金分割法的代码。
二分法:
1 importmath2 importnumpy as np3
4
5 def anyfunction(x): #在这里我们定义任意一个指定初始区间内的单峰函数,以x*cos(x)为例
6 return x*math.cos(x)7
8
9 Low = float(input("Please enter the lowbound:"))10 High = float(input("Please enter the highbound:"))11 High = np.pi #在这里我们取初始上界为π,如果可以输入则注释掉这一行
12 echos = int(input("Please enter the echos:")) #迭代次数
13 small = float(input("Please enter the smallvalue:")) #公式中的Delta
14
15 for i in range(1, echos + 1):16 Lowvalue = anyfunction(0.5*(Low + High -small))17 Highvalue = anyfunction(0.5*(Low + High +small))18 print("echos:" +str(i))19 print('before' + "Lowbound:" + str(0.5*(Low + High - small)) + "Highbound:" + str(0.5*(Low + High +small)))20 print('Lowvalue:' + str(Lowvalue) + ' ' + 'Highvalue:' +str(Highvalue))21 if(Lowvalue ==Highvalue):22 Low = 0.5*(Low + High -small)23 High = 0.5*(Low + High +small)24 elif(Lowvalue
输出结果如下:
5次循环后极值点被限制在[0.7828981633974482,0.8907604338221292]内。
黄金分割法:
1 from math importsqrt, cos2 importnumpy as np3
4
5 def anyfunction(x): #同上以函数x*cos(x)为例
6 return x*cos(x)7
8
9 Low = float(input("Please enter the lowbound:"))10 High = float(input("Please enter the highbound:"))11 High = np.pi #同上,使用时应该注释掉
12 echos = int(input("Please enter the echos:"))13
14 #初始化,第一次运算不存在运算简化
15 uniquevalue = ((sqrt(5)-1)/2)*(High-Low)16 value1 = anyfunction(High -uniquevalue)17 value2 = anyfunction(Low +uniquevalue)18
19 for i in range(1, echos + 1):20 print("echos:" +str(i))21 print('before' + "Lowbound:" + str(High - uniquevalue) + "Highbound:" + str(Low +uniquevalue))22 print('value1:' + str(value1) + ' ' + 'value2:' +str(value2))23 #利用黄金分割法的性质减少一半的运算量
24 if(value1 ==value2):25 Low = High -uniquevalue26 High = Low +uniquevalue27 uniquevalue = ((sqrt(5)-1)/2)*(High-Low)28 value1 = anyfunction(High -uniquevalue)29 value2 = anyfunction(Low +uniquevalue)30 elif(value1
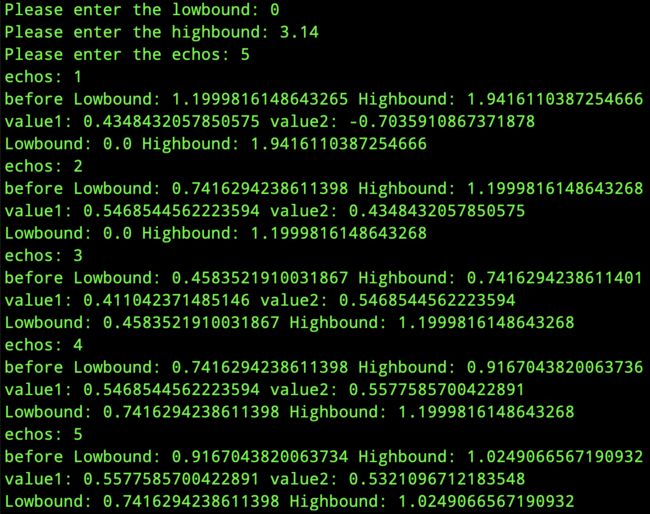
输出结果如下:
5次循环后极值点被限制在[0.7416294238611398,1.0249066567190932]