模拟退火/遗传算法求shubert函数全局极小点
模拟退火/遗传算法求shubert函数全局极小点
-
- shubert函数
- 优化算法
- 模拟退火算法
- 遗传算法
- GA结果
- SA结果
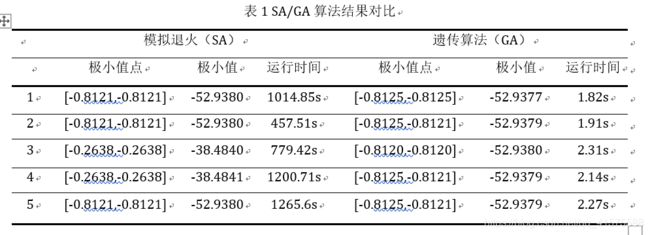
- 算法比较
shubert函数
shubert函数在[-1.1]上有8个局部极小点,其中一个是全局极小点,位于[-0.8121,-0.8121]处

在这里插入图片描述
优化算法
我们使用模拟退火算法和遗传算法求解shubert的全局极小点
模拟退火算法
%****************模拟退火算法求极小点********************
function [Xval1,Yval1]=SimulateAnnealing1
clear all;
close all;
clc;
tic;
tem=30;
step = 0.02;
Xm= 1;%x最大值
Ym = 1;%y最大值
err = 1e-8;
mlen = 10000;% 马尔可夫链长度
sj = 0.95; %衰减参数
accp = 0.0;
rnd =rand;
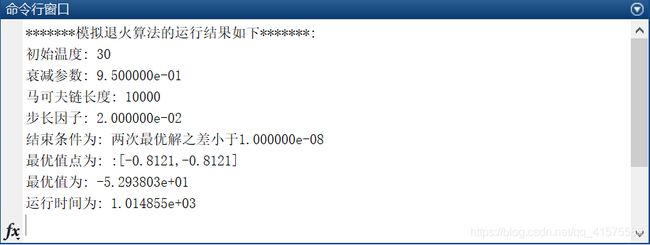
disp('*******模拟退火算法的运行结果如下*******:');
disp(sprintf('初始温度: %d',tem));
disp(sprintf('衰减参数: %d',sj));
disp(sprintf('马尔可夫链长度: %d',mlen));
disp(sprintf('步长因子: %d',step));
disp(sprintf('结束条件为: 两次最优解之差小于%d',err));
% 随机选点 初值设定
Xp = -Xm * rand; %设置初始值
Yp = -Ym * rand;
Xval = Xp;
Yval = Yp;
Xp = -Xm * rand;
Yp = -Ym * rand;
Xval1 = Xp;
Yval1 = Yp;
mm=abs( f( Xval1,Yval1)-f (Xval,Yval));%两次最优解之差
%模拟退火算法
while mm > err
tem=sj*tem;
accp = 0.0;
for i=0:mlen:1 %迭代mlen次
p=0;
while p==0
Xnext = Xp + step*Xm*(rand-0.5);%随机选下一点
NextY = Yp+ step*Ym*(rand-0.5);
if p==(~(Xnext >= -Xm && Xnext <= Xm && NextY>= -Ym && NextY <= Ym))
p=1;
end
end
if (f(Xval1,Yval1) >f(Xnext,NextY))%是否全局最优解
Xval =Xval1;
Yval = Yval1;
Xval1=Xnext;%新的最优解
Yval1=NextY;
end
if( f(Xp,Yp)- f(Xnext,NextY) >0 )
Xp=Xnext;
Yp=NextY;
accp=accp+1;
else
changer = -1 * ( f(Xnext,NextY) -f(Xp,Yp) ) / tem ;
rnd=rand;
p1=exp(changer);
double (p1);
if p1 >rand
Xp=Xnext;
Yp=NextY;
accp=accp+1;
end
end
end
mm=abs( f( Xval1,Yval1)-f (Xval,Yval));
val=f(Xval1, Yval1);
end
disp(sprintf('最优值点为: [%.4f,%.4f]',Xval1,Yval1));
disp(sprintf('最优值为: %d',val));
runtime=toc;
disp(sprintf('运行时间为: %d',runtime));
end
%****************优化函数********************
function value=f(x,y)
value=-cos(2.*x+1).*cos(2.*y+1)-4.*cos(3.*x+2).*cos(3.*y+2)-9.*cos(4.*x+3).*cos(4.*y+3)-16.*cos(5.*x+4).*cos(5.*y+4)-25.*cos(6.*x+5).*cos(6.*y+5);
end
遗传算法
%****************遗传算法求极小点********************
function[X]=hanshuga2
clear all;
close all;
clc;
tic;
pc=0.9;%交叉概率
pm=0.05;%变异概率
n=200;%染色体个数
iter=200; %遗传代数
u=rst(n,44,0,0,0); %生成100*44的染色体矩阵
u1=u(:,1:22);
u2=u(:,23:44);
[N,L]=size(u1);
Xm=-1;xmax=1;%最小值,最大值
Ym=-1;ymax=1;
x0=-1:0.02:1;
y0=-1:0.02:1;
[X,Y]=meshgrid(x0,y0);
f1=-cos(2.*X+1).*cos(2.*Y+1)-4.*cos(3.*X+2).*cos(3.*Y+2)-9.*cos(4.*X+3).*cos(4.*Y+3)-16.*cos(5.*X+4).*cos(5.*Y+4)-25.*cos(6.*X+5).*cos(6.*Y+5);
val=1;
aver=[ ];%各代函数均值
it=1;%遗传迭代量
xval=[ ];yval=[ ];%各代函数最大值
C=[ ];
x=jm(u1,Xm,xmax);
y=jm(u2,Ym,ymax);
f='-cos(2.*x+1).*cos(2.*y+1)-4.*cos(3.*x+2).*cos(3.*y+2)-9.*cos(4.*x+3).*cos(4.*y+3)-16.*cos(5.*x+4).*cos(5.*y+4)-25.*cos(6.*x+5).*cos(6.*y+5)';
fv=eval(f);%计算函数值
%画图
set(0,'defaultfigurecolor','w')
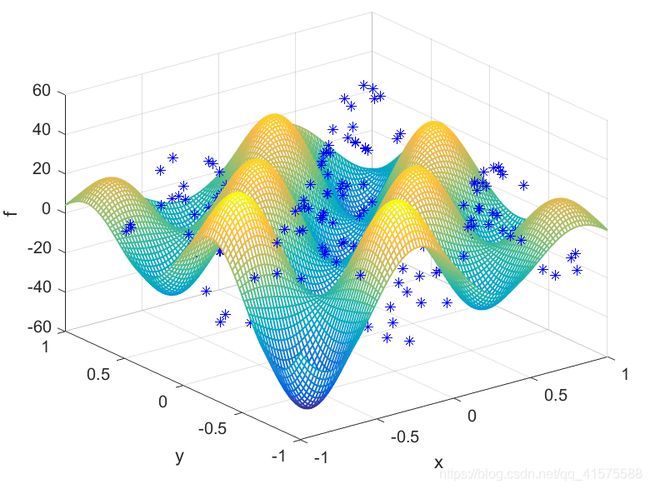
figure(1);%染色体初始位置图1
mesh(X,Y,f1,'LineWidth',1);grid on;hold on;plot3(x,y,fv,'b *');
xlabel('x');ylabel('y');zlabel('f');hold off;
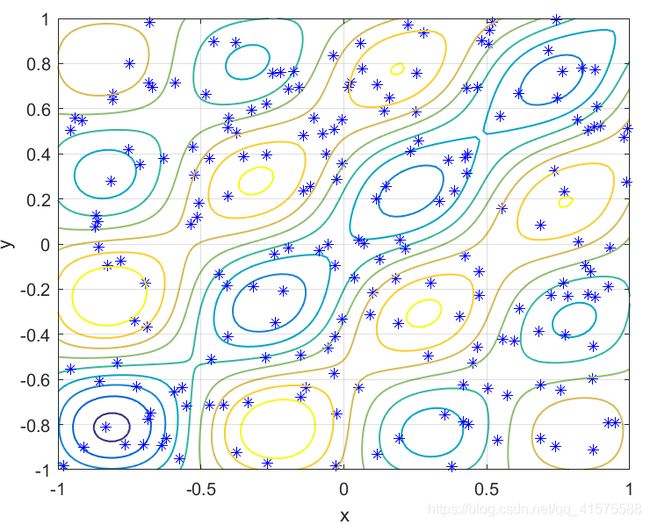
figure(2);%染色体初始位置图2
contour(X,Y,f1,'LineWidth',1);grid on;hold on;plot3(x,y,fv,'b *');
xlabel('x');ylabel('y');zlabel('f');hold off;
pb=0.5;
pw=0.1;
pr=1-(pb+pw); %控制复制
nb=round(pb * N);
nw=round(pw * N);
nr=round(pr * N);
if(nb+nw+nr)~=N, %保证复制后染色体总数不变
dif=N-(nb+nw+nr);
nr=nr+dif;
end;
%生成初始群体
while it <=iter
[rw,ind]=sort(fv);%排序
ind=fliplr(ind);%矩阵左右翻转
vt1=[u1(ind(1:nb),:);u1(ind(end-nw+1:end),:);u1(2:nr+1,:)];%复制操作
vt2=[u2(ind(1:nb),:);u2(ind(end-nw+1:end),:);u2(2:nr+1,:)];
%交叉操作
C(:,1)=rand(N,1)<=pc;%生成50*1矩阵
C(:,2)=round(22. * rand(N,1));
I=find(C(:,1)==1);
IP=[I,C(I,2)];
%vtemp是初始群体集合,交叉操作,生成交叉点
for i=1:size(IP,1),
u1(IP(i,1),:)=[vt1(IP(i,1),1:IP(i,2)) vt1(1,IP(i,2)+1:end)];
u2(IP(i,1),:)=[vt2(IP(i,1),1:IP(i,2)) vt2(1,IP(i,2)+1:end)];
end
%变异操作
m1=rand(N,L)<=pm; %生成50*22矩阵
m2=rand(N,L)<=pm;
m1(1,:)=zeros(1,L); %第一行的染色体不变
m2(1,:)=zeros(1,L);
u1=u1-2.*(u1.*m1)+m1;
u2=u2-2.*(u2.*m2)+m2;
x=jm(u1,Xm,xmax);%解码
y=jm(u2,Ym,ymax);
fv=-eval(f);
[val,indb]=max(fv);%存储第it代的最优值
u1(1,:)=u1(indb,:);%存储最优染色体
u2(1,:)=u2(indb,:);
media=mean(fv);%平均值
xval=[xval val];
yval=[yval val];
aver=[aver media];
it=it+1;
end;
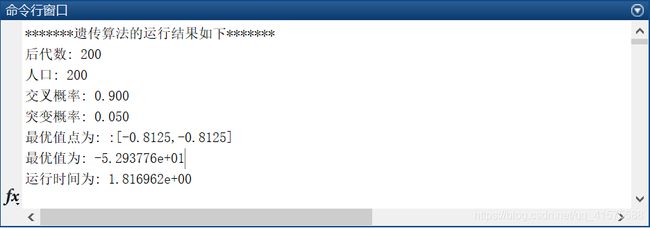
disp(sprintf('*******遗传算法的运行结果如下*******'));
disp(sprintf('后代数: %d',iter));
disp(sprintf('人口: %d',N));
disp(sprintf('交叉概率: %.3f',pc));
disp(sprintf('突变概率: %.3f',pm));
disp(sprintf('最优值点为: [%.4f,%.4f]',x(indb),y(indb)));
disp(sprintf('最优值为: %d',-val));
%画图
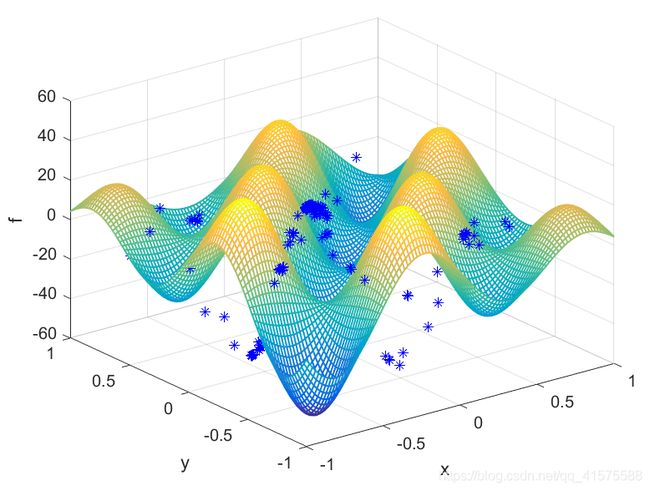
figure(3);%染色体最终位置图1
mesh(X,Y,f1,'LineWidth',1);grid on;hold on;plot3(x,y,fv,'b*');
xlabel(('x'));ylabel('y');zlabel('f');
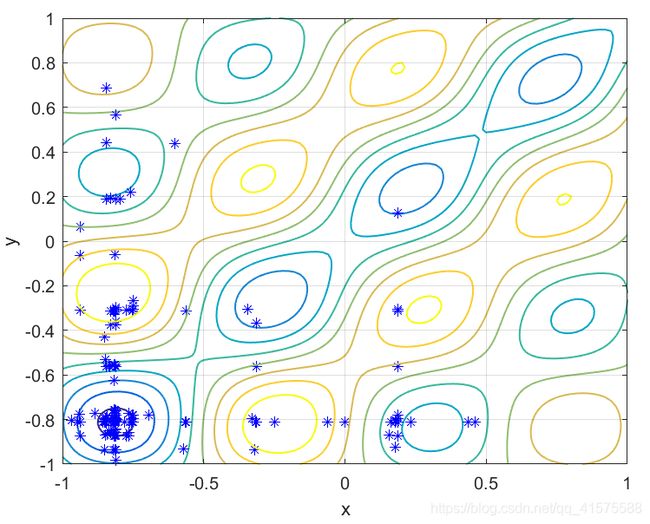
figure(4);%染色体最终位置图2
contour(X,Y,f1,'LineWidth',1);grid on;hold on;plot3(x,y,fv,'b*');
xlabel(('x'));ylabel('y');zlabel('f');
figure(5);%最优值变化图像
plot(-xval,'r *','LineWidth',1);xlabel('Generations');ylabel('value');
figure(6)%平均值变化图像
plot(-aver,'b','LineWidth',1);xlabel('Generations');ylabel('average value');hold off;
runtime=toc
disp(sprintf('运行时间为: %d',runtime));
function x=jm(v1,xmin,xmax); %decode解码
v1=fliplr(v1);%矩阵的左右翻转
s=size(v1);%
aux=0:1:21;aux=ones(s(1),1)*aux;
x1=sum((v1.*2.^aux)');
x=xmin+(xmax-xmin)*x1./4194303;
%**********生成染色体矩阵(长度*个数)************
function[m,n]=rst(n1,s1,n2,s2,bip)
if nargin==2
n2=n1;s2=s1;bip=1;
elseif nargin==4,
bip=1;
end;
m=2.*rand(n1,s1)-1; %rand(n1,s1)表示生成n1 X s1的值为0-1的任意矩阵
if bip==1,
m=hardlims(m);
else;
m=hardlim(m);
end;
n=2.*rand(n2,s2)-1;
if bip==1,
n=hardlims(n);
else;
n=hardlim(n);
end;
###解码
function y=jm(v2,ymin,ymax);
v2=fliplr(v2);%矩阵的左右翻转
vs=size(v2);
aux=0:1:21;aux=ones(s(1),1)*aux;
y1=sum((v2.*2.^aux)');
y=ymin+(ymax-ymin)*y1./4194303;