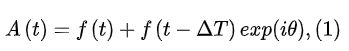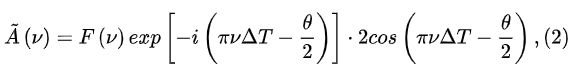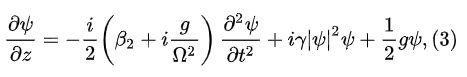光纤激光器仿真：(2)孤子分子及其转换动力学
孤子分子
类似于化学反应中通过强力的化学键链接组合实现原子之间平衡的分子，孤子分子（soliton molecules）作为一种束缚的孤子形态，由多个子脉冲组成，它是非线性效应，色散效应，增益和损耗等许多效应复杂作用引起的孤子之间的斥力和引力平衡的结果。它还有些别称如孤子束缚态（Soliton bound states）、多孤子态（Multisoliton states）、多脉冲态（Multi-pulsing states）。由于被动锁模光纤激光器只能承受一定程度的非线性相移，高泵浦功率会导致腔内脉冲分裂和多个脉冲共存，这种平衡导致几个相同的脉冲(完全相同的强度，以及相同的光谱和时间分布)被捆绑起来，并在相邻脉冲之间保持恒定的时间间隔和固定的相位差。孤子分子对于理解和探索锁模光纤激光器内在物理机制具有重要意义。原因有两方面：一方面，它们是光纤激光器中最经常观察到的复杂非线性动力学现象，这有助于我们探索潜在的耗散性质；另一方面，它们对于开发光纤传输线路中更大的通信容量尤其有用，并推进实时光谱学（real-time spectroscopy）等超快表征方法。
自从孤子分子首次被Malomed教授在非线性薛定谔-金兹堡-朗道方程（nonlinear Schrödinger-Ginzburg-Landau equation）和耦合非线性薛定谔方程（coupled nonlinear Schrödingerequations）的框架下理论预测[1][2]。利用非线性偏振演化（Nonlinear polarization evolution，NPE），非线性放大环形镜（nonlinear amplifying loop mirror，NALM）以及真实可饱和吸收体等锁模结构的锁模光纤激光器的大量实验都观测到了孤子分子。接下来的部分将对孤子分子进行仿真。
简单解析解（含关键源代码）
这里考虑简单双孤子束缚态（Two-soliton bound states）的光场表达式，双孤子束缚态可以看作由具有一定相位差和脉冲间隔的两个孤子构成。因此它的时域表达式可以写成
傅里叶变换后的频域表达式可写成
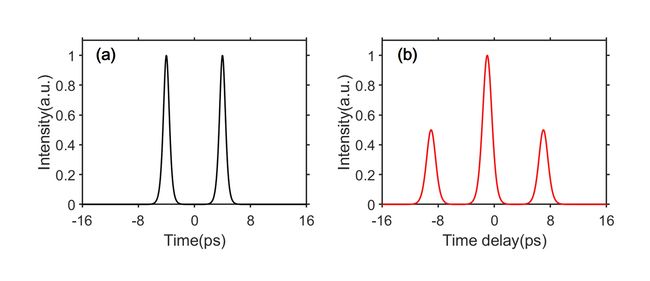
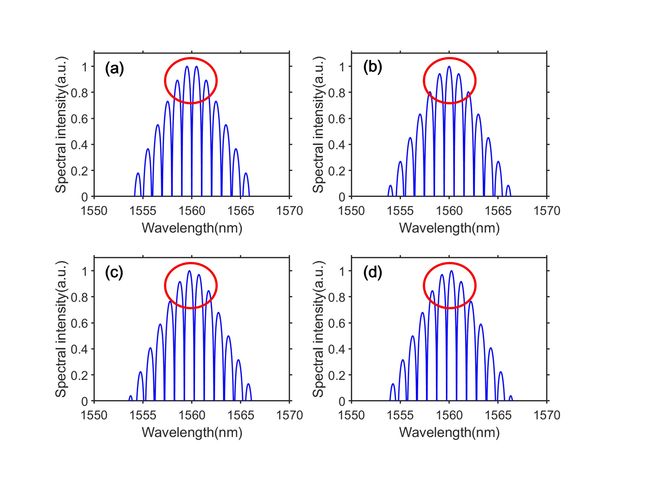
需要注意的，相位差的作用可以改变频谱的中心强度的分布。当相位差为0或者pi时为中心对称分布，其它角度的相位差时则不对称。这里展示双孤子束缚态的时域和频域形态如图1和图2所示。
图1 双孤子束缚态的(a)时域和(b)自相关
图2 双孤子束缚态的dB频域(a)pi；(b)0；(c)-pi/2；(d)pi/2
关键源代码
u = sqrt(P0).*sech((t+dt2)/T0)...
+ sqrt(P0).*sech((t-dt2)/T0).*exp(1i.*pha1);%sech型双孤子束缚态通常来说，对于多孤子束缚态不再采用这种简单解析解的形式，因其内部作用更加复杂，因此往往进行光纤激光器仿真来实现。
数值仿真模型与结果
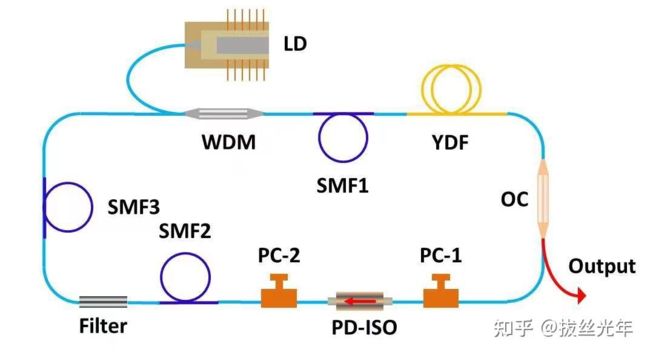
这里利用如下前文的全正色散光纤激光器结构，通过增大泵浦功率促使其分裂并改变偏振态，可以得到双孤子束缚态和多孤子束缚态。前文链接如下
光纤激光器仿真: (1)耗散孤子以及耗散孤子共振
激光腔结构如图3所示。
图3 激光腔结构
仿真光纤所用的金兹堡-朗道方程为
双孤子束缚态
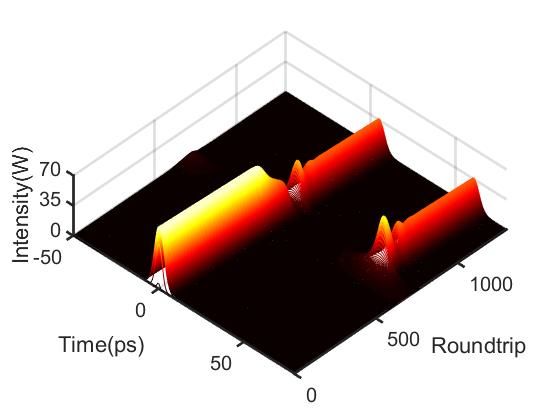
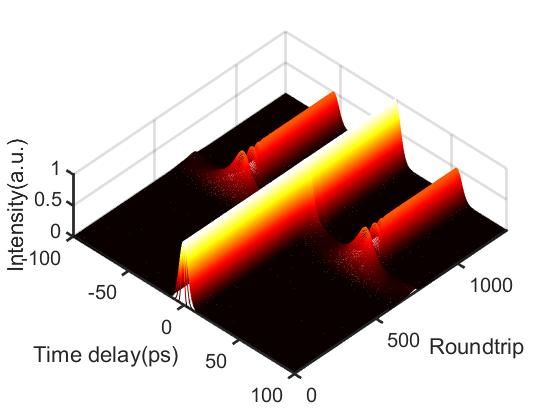
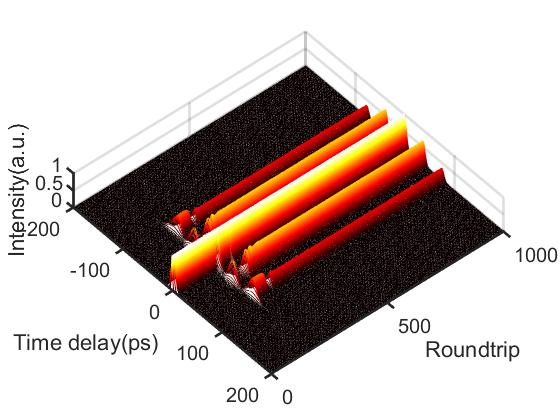
为了更快锁定，这里采用弱高斯脉冲作为输入（噪声也可），得到双孤子束缚态的时域演化图如图4所示，可以看到初始时随着腔内循环，输入脉冲能量增大，保持一定圈数的亚稳态单孤子在一定时延位置处分裂出新的子脉冲，从而形成双孤子束缚态。在稳定的双孤子束缚态形成之前，不难发现束缚态的两个子脉冲会发生跳动，导致峰值功率的轻微增加，这也反映了增益竞争（gain competition）的作用。图5展示了双孤子束缚态的自相关演化图，也在同样的循环圈数时产生类似变化。
图4 双孤子束缚态的时域演化图
图5 双孤子束缚态的自相关yan'hu
多孤子束缚态
三孤子束缚态
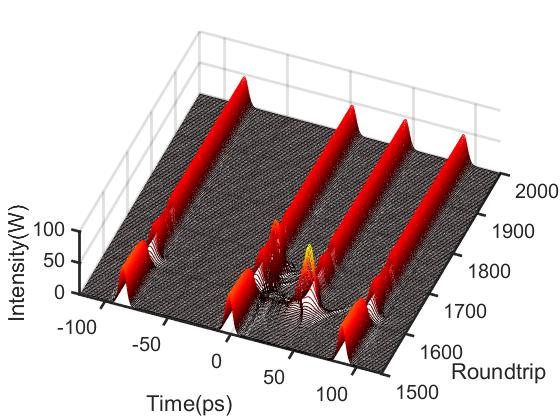
（进一步增大增益饱和能量/泵浦功率）图6展示了三孤子束缚态的时域演化图。不同于双孤子束缚态，亚稳态的单孤子分裂并在前后时延位置处都产生新的子脉冲，并在两个子脉冲中间逐步演化出新的子脉冲，从而形成三孤子束缚态，这也很好地验证了Zeng等人的OL实验工作[3]。图7展示了三孤子束缚态的自相关演化图。
图6 三孤子束缚态的时域演化图
图7 三孤子束缚态的自相关演化图
四孤子束缚态
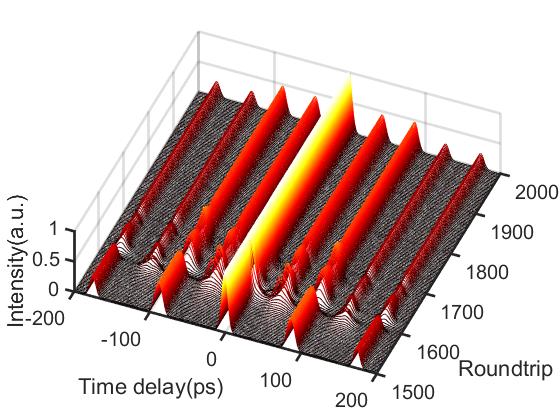
（更进一步增大增益饱和能量/泵浦功率）图8和图9展示了四孤子束缚态的时域和自相关演化图。由于需要较长循环圈数达到稳定，这里截取了1500-2000圈的图如下所示。增益动力学（gain dynamics）主要引起其能量的波动，随着净腔增益和损耗动力学结合可饱和吸收效应的平衡，最终达到稳定的锁模状态。
图8 四孤子束缚态的时域演化图
图9 四孤子束缚态的自相关演化图
剖面图细节
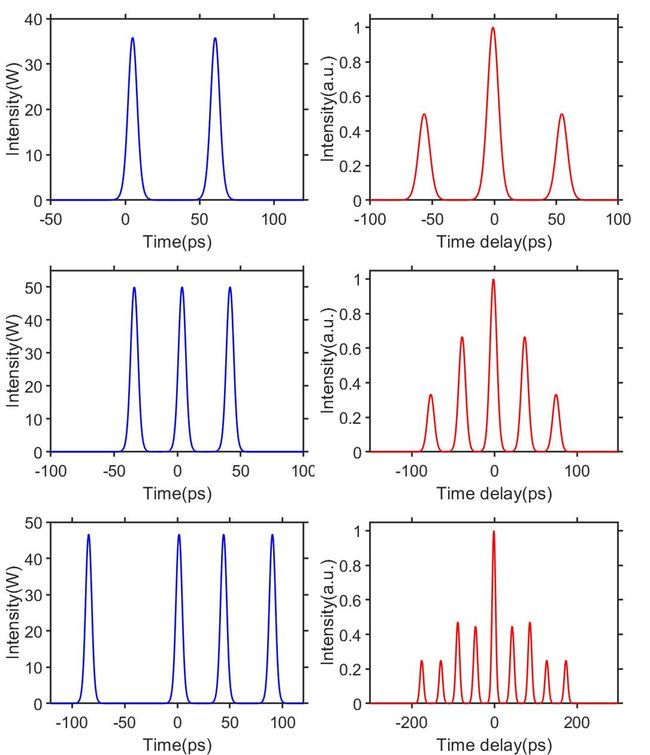
图10展示了双孤子束缚态~四孤子束缚态的时域和自相关剖面图。
图10 时域和自相关剖面图
本文所用图为本人在MATLAB上仿真的程序所画，如要转载引用，请注明出处。如有问题，欢迎咨询讨论。欢迎大家关注我的公众号：超级光学。一个专注分享光学前沿科研资讯和光学仿真知识干货的专业平台～
参考
[1] Malomed B A. Bound solitons in the nonlinear Schrödinger/Ginzburg-Landau equation[M]//Large Scale Structures in Nonlinear Physics. Springer, Berlin, Heidelberg, 1991: 288-294.
[2] Malomed B A . Bound solitons in coupled nonlinear Schrödinger equations[J]. Phys.rev.a, 1992, 22(4):403-439.
[3] Zeng J, Sander M Y. Real-time transition dynamics between multi-pulsing states in a mode-locked fiber laser[J]. Optics Letters, 2020, 45(1): 5-8.