强化学习算法:AC系列详解
文章目录
- AC
- A2C
- A3C
- References
AC
Actor-Critic算法分为两部分,actor的前身是policy gradient,它可以轻松地在连续动作空间内选择合适的动作,value-based的Q-learning只能解决离散动作空间的问题。但是又因为Actor是基于一个episode的return来进行更新的,所以学习效率比较慢。这时候我们发现使用一个value-based的算法作为Critic就可以使用TD方法实现单步更新,这其实可以看做是拿偏差换方差。这样两种算法相互补充就形成了我们的Actor-Critic。
Actor 基于概率分布选择行为, Critic 基于 Actor 生成的行为评判得分, Actor 再根据 Critic 的评分修改选行为的概率。
- 优点:可以进行单步更新,不需要跑完一个episode再更新网络参数,相较于传统的PG更新更快。传统PG对价值的估计虽然是无偏的,但方差较大,AC方法牺牲了一点偏差,但能够有效降低方差;
- 缺点:Actor的行为取决于 Critic 的Value,但是因为 Critic本身就很难收敛和actor一起更新的话就更难收敛了。(为了解决收敛问题, Deepmind 提出了 Actor Critic 升级版 Deep Deterministic Policy Gradient,后者融合了 DQN 的一些 trick, 解决了收敛难的问题)。
AC算法与策略梯度法在第一步生成样本和第三步策略改进上并没有显著区别,主要区别在于第二步:我们现在尝试去拟合一个值函数(Q,V,A都行),以期能得到一个更好的梯度估计。我们真正从policy gradient的“估计收益”变为了“拟合模型”。
Q函数取决于状态和行为两个维度,因此输入是对应两个空间的笛卡尔积。但是维度越大,同样的样本数估计的方差越大。给定当前的状态和行为,当前的收益就确定了,可以把当前的收益提出来:
Q π ( s t , a t ) = r ( s t , a t ) + ∑ t ′ = t + 1 T E π θ [ r ( s t ′ , a t ′ ) ∣ s t , a t ] Q^\pi(s_t,a_t)=r(s_t,a_t)+\sum_{t'=t+1}^T\mathbb{E}_{\pi_\theta}[r(s_{t'},a_{t'})|s_t,a_t] Qπ(st,at)=r(st,at)+t′=t+1∑TEπθ[r(st′,at′)∣st,at]
而后边那块求和项其实就是值函数的期望:
E s t + 1 ∼ p ( s t + 1 ∣ s t , a t ) [ V π ( s t + 1 ) ] \mathbb{E}_{s_{t+1}\sim p(s_{t+1}|s_t,a_t)}[V^\pi(s_{t+1})] Est+1∼p(st+1∣st,at)[Vπ(st+1)]
如果我们愿意做一点近似,用轨迹样本来估计这个期望——此时不是使用整条轨迹,而仅仅是看一步以后的状态,那么我们的Q函数可以近似为:
Q π ( s t , a t ) ≈ r ( s t , a t ) + V π ( s t + 1 ) Q^\pi(s_t,a_t)\approx r(s_t,a_t)+V^\pi(s_{t+1}) Qπ(st,at)≈r(st,at)+Vπ(st+1)
与此同时,优势函数也可以被近似为:
A π ( s t , a t ) ≈ r ( s t , a t ) + V π ( s t + 1 ) − V π ( s t ) A^\pi(s_t,a_t)\approx r(s_t,a_t)+V^\pi(s_{t+1})-V^\pi(s_{t}) Aπ(st,at)≈r(st,at)+Vπ(st+1)−Vπ(st)
这么一来,其实我们只要去拟合值函数V就好,其他的都可以被近似表示,这样拟合神经网络的维度的输入空间就只需要是状态空间了。因为实用性和便利性,绝大多数的AC算法都是仅训练一个critic神经网络V(而非Q+V),使得输入状态为 s s s,输出给定策略下值函数的估计量 V ^ π ( s ) \hat{V}^\pi(s) V^π(s)。
critic网络的训练数据与损失如下:

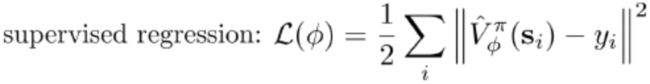
批量和在线的AC算法流程图如下所示,注意这两个都是on-policy算法:

A2C
上述AC方法中,使用状态价值函数作为baseline的方法,即使用优势函数 A A A代替累积收益 G G G(或是行为价值函数 Q Q Q),称之为Advantage Actor-Critic (A2C)(AC部分最后的算法图其实就是A2C)。优势函数还有一个好处, Q − V Q-V Q−V可以反应当前状态下某一行为下的价值相对于平均价值的好坏,从而使得结果有正有负,梯度更新后会使得更新后的策略尽量避免选择这些结果为负的形态行为对,使得更新后的策略分布方差更小。
注意:REINFORECE等很多policy-based算法也会去估计值函数,但它们不是actor-critic方法,因为其中的价值函数网络并没有作为策略网络更新的目标,而仅仅是作为baseline出现的。只要价值函数网络以任何形式出现在目标中(即原来 G t G_t Gt的位置上),都是actor-critic方法,下图列出了各种不同actor-critic方法用到的策略梯度。

A3C
A3C是异步版本的A2C算法,其异步的方法是使用带不同探索参数的不同的CPU来采样,每个CPU上的采样积累到一定的数量之和再一起拿去更新网络参数。具体的示意图和算法如下图所示。

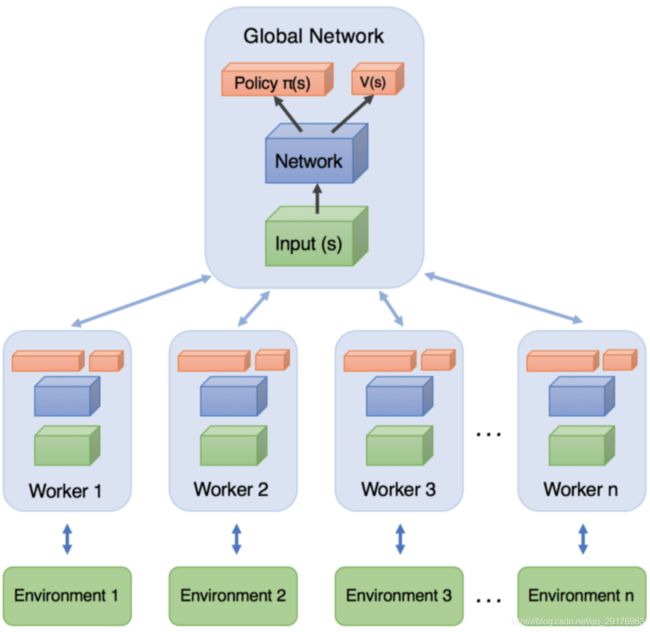

A3C有一个主网络,n个worker线程,每个线程里有和公共的主网络一样的网络,也是一个A2C网络,每个线程会独立的和环境进行交互得到经验数据,这些线程之间互不干扰,独立运行。从伪代码中可以看出A3C主要包括如下几个部分:
- 将主网络参数复制到n个子网络中;
- 子网络与环境交互产生样本;
- 抽取样本,计算子网络(策略网络与价值网络)的梯度并累积求和(与A2C方法一致);
- 使用得到的累积梯度更新主网络(策略网络与价值网络),回到步骤1进入下一个loop。
其实从伪代码可以看出A3C和A2C在更新参数的时候并不太一样,A3C是一种n-step的方法(降低方差的同时也降低了偏差),而A2C是一种1-step方法。
A3C的优点:
- 强化学习算法不稳定很大程度上是由于强化学习得到一连串的数据之间具有相关性,只有打破只有的相关性才能得到一个稳定的算法。前面了解到的DQN就是使用了经验池的方法来打破数据时间的相关性,通过从经验池里面采样,使得相关性较低的样本能够在同一个batch里面用来更新价值函数。这里使用了异步的方法来打破数据之间的相关性,多个actor探索到的经历不同,这样actor之间的样本相关性就降低了,从而稳定了算法。而且经验池的使用要求使用off-policy的方法,而采取异步的方法则可以使用更稳定的on-policy方法。
- 在不同的actor上能够分别采用不同的探索参数(如果不同actor探索参数不一致,感觉就得采用off-policy了),从而增加全局探索的多样性;同时,实际上不同的actor也能够去探索环境的不同部分。
注意:本篇博客所讲算法都是on-policy的。
最后对于AC方法心里有个小疑问:在AC方法更新策略网络和价值网络时(例如A3C伪代码的倒数第四第五行),如果没有target价值网络的话,更新公式中它们都会包含 ( R − V ( s i ∣ θ v ′ ) ) (R-V(s_i|\theta_v')) (R−V(si∣θv′)),价值网络的梯度更新会倾向于使这一项为0,而策略网络需要使用这一项的值来计算梯度,这会不会导致网络难收敛等问题。
一点想法: ( R − V ( s i ∣ θ v ′ ) ) (R-V(s_i|\theta_v')) (R−V(si∣θv′))会得到当前行状态为价值相对于平均状态价值的好坏,我们希望策略梯度往 ( R − V ( s i ∣ θ v ′ ) ) (R-V(s_i|\theta_v')) (R−V(si∣θv′))大的方向更新;在计算价值网络梯度时,在当前策略下, V ( s i ∣ θ v ′ ) V(s_i|\theta_v') V(si∣θv′)应该等于 R R R,因此更新梯度,希望使得 R − V ( s i ∣ θ v ′ ) = 0 R-V(s_i|\theta_v')=0 R−V(si∣θv′)=0。即整个流程都是按Bellman期望方程更新的。
(感觉还是有点迷迷糊糊,希望大家能指正。)
References
[1] CSDN:【强化学习】Actor-Critic算法详解
[2] 知乎:【强化学习入门 3】强化学习策略梯度类方法
[3] CDSN:深度强化学习8——Actor-Critic(AC、A2C、A3C)
