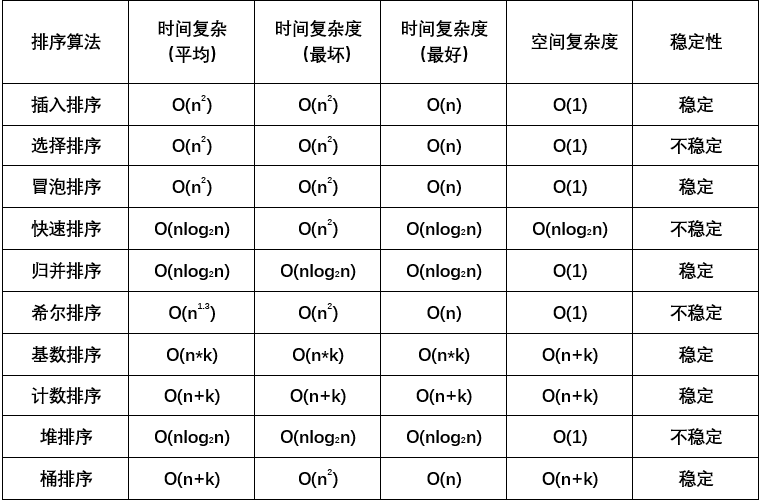
用python排序算法_Python十大经典排序算法
现在很多的事情都可以用算法来解决,在编程上,算法有着很重要的地位,将算法用函数封装起来,使程序能更好的调用,不需要反复编写。
Python十大经典算法:
一、插入排序
1.算法思想
从第二个元素开始和前面的元素进行比较,如果前面的元素比当前元素大,则将前面元素 后移,当前元素依次往前,直到找到比它小或等于它的元素插入在其后面,
然后选择第三个元素,重复上述操作,进行插入,依次选择到最后一个元素,插入后即完成所有排序。
2.代码实现
1 definsertion_sort(arr):2 #插入排序
3 #第一层for表示循环插入的遍数
4 for i in range(1, len(arr)):5 #设置当前需要插入的元素
6 current =arr[i]7 #与当前元素比较的比较元素
8 pre_index = i - 1
9 while pre_index >= 0 and arr[pre_index] >current:10 #当比较元素大于当前元素则把比较元素后移
11 arr[pre_index + 1] =arr[pre_index]12 #往前选择下一个比较元素
13 pre_index -= 1
14 #当比较元素小于当前元素,则将当前元素插入在 其后面
15 arr[pre_index + 1] =current16 return arr
二、选择排序
1.算法思想
设第一个元素为比较元素,依次和后面的元素比较,比较完所有元素找到最小的元素,将它和第一个元素互换,重复上述操作,我们找出第二小的元素和第二个位置的元素互换,以此类推找出剩余最小元素将它换到前面,即完成排序。
2.代码实现
1 defselection_sort(arr):2 #选择排序
3 #第一层for表示循环选择的遍数
4 for i in range(len(arr) - 1):5 #将起始元素设为最小元素
6 min_index =i7 #第二层for表示最小元素和后面的元素逐个比较
8 for j in range(i + 1, len(arr)):9 if arr[j]
11 min_index =j12 #查找一遍后将最小元素与起始元素互换
13 arr[min_index], arr[i] =arr[i], arr[min_index]14 return arr
三、冒泡排序
1.算法思想
从第一个和第二个开始比较,如果第一个比第二个大,则交换位置,然后比较第二个和第三个,逐渐往后,经过第一轮后最大的元素已经排在最后,
所以重复上述操作的话第二大的则会排在倒数第二的位置。,那重复上述操作n-1次即可完成排序,因为最后一次只有一个元素所以不需要比较。
2.代码实现
1 defbubble_sort(arr):2 #冒泡排序
3 #第一层for表示循环的遍数
4 for i in range(len(arr) - 1):5 #第二层for表示具体比较哪两个元素
6 for j in range(len(arr) - 1 -i):7 if arr[j] > arr[j + 1]:8 #如果前面的大于后面的,则交换这两个元素的位置
9 arr[j], arr[j + 1] = arr[j + 1], arr[j]10 return arr
四、快速排序
1.算法思想
找出基线条件,这种条件必须尽可能简单,不断将问题分解(或者说缩小规模),直到符合基线条件。
2.代码实现
1 defquick_sort(arr):2 if len(arr) < 2:3 #基线条件:为空或只包含一个元素的数组是“有序”的
4 returnarr5 else:6 #递归条件
7 pivot =arr[0]8 #由所有小于基准值的元素组成的子数组
9 less = [i for i in arr[1:] if i <=pivot]10 #由所有大于基准值的元素组成的子数组
11 greater = [i for i in array[1:] if i >pivot]12 return quicksort(less) + [pivot] +quicksort(greater)13
14 print(quick_sort([10, 5, 2, 3]))
五、归并排序
1.算法思想
归并排序是分治法的典型应用。分治法(Divide-and-Conquer):将原问题划分成 n 个规模较小而结构与原问题相似的子问题;递归地解决这些问题,然后再合并其结果,就得到原问题的解,分解后的数列很像一个二叉树。
具体实现步骤:
使用递归将源数列使用二分法分成多个子列
申请空间将两个子列排序合并然后返回
将所有子列一步一步合并最后完成排序
注:先分解再归并
2.代码实现
1 defmerge_sort(arr):2 #归并排序
3 if len(arr) == 1:4 returnarr5 #使用二分法将数列分两个
6 mid = len(arr) // 2
7 left =arr[:mid]8 right =arr[mid:]9 #使用递归运算
10 returnmarge(merge_sort(left), merge_sort(right))11
12
13 defmarge(left, right):14 #排序合并两个数列
15 result =[]16 #两个数列都有值
17 while len(left) > 0 and len(right) >0:18 #左右两个数列第一个最小放前面
19 if left[0] <=right[0]:20 result.append(left.pop(0))21 else:22 result.append(right.pop(0))23 #只有一个数列中还有值,直接添加
24 result +=left25 result +=right26 return result
六、希尔排序
1.算法思想
希尔排序的整体思想是将固定间隔的几个元素之间排序,然后再缩小这个间隔。这样到最后数列就成为了基本有序数列。
具体步骤:
计算一个增量(间隔)值
对元素进行增量元素进行比较,比如增量值为7,那么就对0,7,14,21…个元素进行插入排序
然后对1,8,15…进行排序,依次递增进行排序
所有元素排序完后,缩小增量比如为3,然后又重复上述第2,3步
最后缩小增量至1时,数列已经基本有序,最后一遍普通插入即可
2.代码实现
1 defshell_sort(arr):2 #希尔排序
3 #取整计算增量(间隔)值
4 gap = len(arr) // 2
5 while gap >0:6 #从增量值开始遍历比较
7 for i inrange(gap, len(arr)):8 j =i9 current =arr[i]10 #元素与他同列的前面的每个元素比较,如果比前面的小则互换
11 while j - gap >= 0 and current < arr[j -gap]:12 arr[j] = arr[j -gap]13 j -=gap14 arr[j] =current15 #缩小增量(间隔)值
16 gap //= 2
17 return arr
七、基数排序
1.算法思想
基数排序(radix sort)属于“分配式排序”(distribution sort),又称“桶子法”(bucket sort)或bin sort,顾名思义,它是透过键值的部份资讯,将要排序的元素分配至某些“桶”中,藉以达到排序的作用,基数排序法是属于稳定性的排序,其时间复杂度为O (nlog(r)m),其中r为所采取的基数,而m为堆数,在某些时候,基数排序法的效率高于其它的稳定性排序法。
2.代码实现
2.1由桶排序改造,从最低位到最高位依次桶排序,最后输出最后排好的列表。
1 defRadixSort(list,d):2 for k in range(d):#d轮排序
3 #每一轮生成10个列表
4 s=[[] for i in range(10)]#因为每一位数字都是0~9,故建立10个桶
5 for i inlist:6 #按第k位放入到桶中
7 s[i//(10**k)%10].append(i)8 #按当前桶的顺序重排列表
9 list=[j for i in s for j ini]10 return list
2.2简单实现
1 from random importrandint2 defradix_sort():3 A = [randint(1, 99999999) for _ in xrange(9999)]4 for k in xrange(8):5 S = [ [] for _ in xrange(10)]6 for j inA:7 S[j / (10 ** k) % 10].append(j)8 A = [a for b in S for a inb]9 for i inA:10 print i
八、计数排序
1.算法思想
对每一个输入元素x,确定小于x的元素个数。利用这一信息,就可以直接把x 放在它在输出数组上的位置上了,运行时间为O(n),但其需要的空间不一定,空间浪费大。
2.代码实现
1 from numpy.random importrandint2 defConuting_Sort(A):3 k = max(A) #A的最大值,用于确定C的长度
4 C = [0]*(k+1) #通过下表索引,临时存放A的数据
5 B = (len(A))*[0] #存放A排序完成后的数组
6 for i inrange(0, len(A)):7 C[A[i]] += 1 #记录A有哪些数字,值为A[i]的共有几个
8 for i in range(1, k+1):9 C[i] += C[i-1] #A中小于i的数字个数为C[i]
10 for i in range(len(A)-1, -1, -1):11 B[C[A[i]]-1] = A[i] #C[A[i]]的值即为A[i]的值在A中的次序
12 C[A[i]] -= 1 #每插入一个A[i],则C[A[i]]减一
13 return B
九、堆排序
1.算法思想
堆分为最大堆和最小堆,是完全二叉树。堆排序就是把堆顶的最大数取出,将剩余的堆继续调整为最大堆,具体过程在第二块有介绍,以递归实现 ,
剩余部分调整为最大堆后,再次将堆顶的最大数取出,再将剩余部分调整为最大堆,这个过程持续到剩余数只有一个时结束。
2.代码实现
1 importtime,random2 defsift_down(arr, node, end):3 root =node4 #print(root,2*root+1,end)
5 whileTrue:6 #从root开始对最大堆调整
7 child = 2 * root +1 #left child
8 if child >end:9 #print('break',)
10 break
11 print("v:",root,arr[root],child,arr[child])12 print(arr)13 #找出两个child中交大的一个
14 if child + 1 <= end and arr[child] < arr[child + 1]: #如果左边小于右边
15 child += 1 #设置右边为大
16 if arr[root]
18 tmp =arr[root]19 arr[root] =arr[child]20 arr[child]=tmp21 #正在调整的节点设置为root
22 #print("less1:", arr[root],arr[child],root,child)
23 root = child #24 #[3, 4, 7, 8, 9, 11, 13, 15, 16, 21, 22, 29]
25 #print("less2:", arr[root],arr[child],root,child)
26 else:27 #无需调整的时候, 退出
28 break
29 #print(arr)
30 print('-------------')31
32 defheap_sort(arr):33 #从最后一个有子节点的孩子还是调整最大堆
34 first = len(arr) // 2 -1
35 for i in range(first, -1, -1):36 sift_down(arr, i, len(arr) - 1)37 #[29, 22, 16, 9, 15, 21, 3, 13, 8, 7, 4, 11]
38 print('--------end---',arr)39 #将最大的放到堆的最后一个, 堆-1, 继续调整排序
40 for end in range(len(arr) -1, 0, -1):41 arr[0], arr[end] =arr[end], arr[0]42 sift_down(arr, 0, end - 1)43 #print(arr)
十、桶排序
1.算法思想
为了节省空间和时间,我们需要指定要排序的数据中最小以及最大的数字的值,来方便桶排序算法的运算。
2.代码实现
1 #桶排序
2 defbucket_sort(the_list):3 #设置全为0的数组
4 all_list = [0 for i in range(100)]5 last_list =[]6 for v inthe_list:7 all_list[v] = 1 if all_list[v]==0 else all_list[v]+1
8 for i,t_v inenumerate(all_list):9 if t_v !=0:10 for j inrange(t_v):11 last_list.append(i)12 return last_list
总结:
在编程中,算法都是相通的,算法重在算法思想,相当于将一道数学上的应用题的每个条件,区间,可能出现的结果进行分解,分步骤的实现它。算法就是将具体问题的共性抽象出来,将步骤用编程语言来实现。通过这次对排序算法的整理,加深了对各算法的了解,具体的代码是无法记忆的,通过对算法思想的理解,根据伪代码来实现具体算法的编程,才是真正了解算法。