【深度强化学习】6. Q-Learning技巧及其改进方案

【DataWhale打卡】第四次任务，主要是重新学习一下李宏毅的Q-learning部分的知识，推导很多。之前看的时候就是简单过了一遍，很多细节没有清楚。这篇笔记包括了李宏毅深度强化学习三个视频长度的内容。

1. 概念/解释

概念	解释
Critic	与Actor不同，Critic负责评论当前的行为，预测期望价值
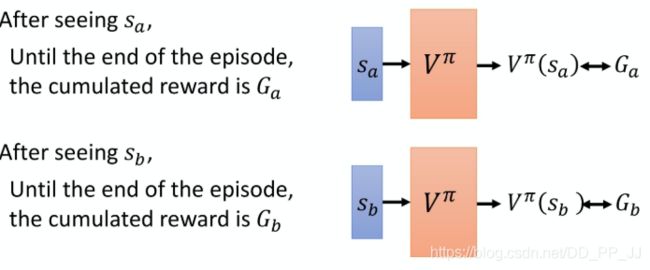
$V^{\pi }(s)$	在遇到状态s以后，可以得到的累计奖励值（这个值和s、$\pi$均有关系）
$Q^{\pi }(s,a)$	使用$\pi$作为actor的时候，在状态s下采取动作a的期望的累计奖励（cumulated reward）。
DQN	Q-Learning+深度学习（采用了TargetNetwork和Experience Replay的方法训练）
Q-function	即在某一个 state 采取某一个action，使用 actor $\pi$ ，得到的 accumulated reward 的期望值有多大

2. Value Function

MC估计V

Monte-Carlo 方法，通过采样来近似得到Value函数。

在遇到不同state的情况下，计算对应的accumulated reward $G_t$。在训练的过程就是一个回归问题，将value function的值回归到$G_t$。

TD 估计V
$$V^{\pi }\left(s_t\right)=V^{\pi }\left(s_{t+1}\right)+r_t$$
基于以上式子，只要有任意一个s,a,r,s的片段，就可以用来训练。训练过程如下图所示：

对比两种方法

• MC存在很大的Variance，因为是累积的reward，这样会导致Larger Variance。

• TD虽然有着smaller variance,但是$V^{\pi }(s_{t+1})$有可能是不准确的。

TD由于其灵活性，数据可以重复利用，所以比较常见。

举个计算的例子：

3. State-Action Value Function

引入另外一种critic，Q-function（State-Action Value Function）。

Value Function仅仅通过看到的状态s就开始判断价值，这里引入动作a，意义是$Q^{\pi }(s,a)$ 代表使用$\pi$作为actor的时候，在状态s下采取动作a的期望的累计奖励（cumulated reward）。

思考：$\pi$本身会决定在遇到s的时候，应该采取哪个action，那么这里的Q怎么理解呢？

其实就是在state s的时候强制采取action a，然后得到的垒起奖励，才是$Q^{\pi }(s,a)$

第一篇文章中就有讲action space分为离散的（discrete）和连续的（continuous）

上图左侧代表输出的是一个数值。右侧代表在状态s下，采取不同的action所对应的Q函数。

Q-Learning一般流程

Q-Learning这种方式和policy gradient不同：

• Policy gradient的目标就是学习策略$\pi$, 给定一个s就可以输出选择的动作a。
• Q-Learning则是以一种间接的方法实现了这个目的。在给定一个状态s后，如果有了Q函数，那就可以决定采取哪个function可以得到的期望值更高。

描述一下整个流程，初始的$\pi$和环境进行交互（一开始随机初始化的策略肯定很差），然后会收集一系列episode带来的数据。然后去衡量这个actor在某一个s强制采取a以后的期望，计算Q Value。学习得到的Q函数得到的新策略${\pi }^{\prime }$是一定要比原actor策略更好的。

这样迭代下去，可以保证policy是越来越好的。

那么新策略${\pi }^{\prime }$是如何指定的？

• 策略是通过最大化Q Function得到的，所以可以保证在同一个状态s下，新的策略不比旧的策略差。
• 这里的策略和policy gradient不一样，并没有参数。是通过Q function来计算得到的。
• 需要说明的是，由于采用了argmax的形式，那也就是默认action space是离散的，单纯的Q-Learning无法解决连续动作空间的问题，随后会提出新的算法解决这个问题。

推到步骤如下：

4. TIP: Target Network

具体怎么实现？

通过actor与环境交互，得到一系列轨迹，s,a,r,s，通过以下公式回归求解问题：
$${\mathrm{Q}}^{\pi }\left(s_t,a_t\right)=r_t+{\mathrm{Q}}^{\pi }\left(s_{t+1},\pi \left(s_{t+1}\right)\right)$$
实际回归的时候，会发现由于左右两边都在变化，这样训练会很不稳定。这个问题解决方案是：固定右边的Q-Network（负责产生target,所以叫做target network），只update左边的Q-Network的参数。然后每过N次，将左侧Q-Network的参数复制给Target Network, 然后重新训练。

5. TIP: Exploration

Exploration在第一篇中就提到过，为了让actor能更好的探索环境，而不是拘泥于之前的经验中。对于Q-function来说，这样可以更好的收集到所有的s,a组成的pair。

一般采用两种方法：

• Epsilon Greedy: 如上图公式，设置一个很小的$ϵ$, 以这个为概率进行随即探索。
• Boltzmann Exploration: 这个和Policy Gradient比较相似，Policy Gradient中是生成概率分布，依照概率进行采样，引入了随机性。这里用上图中的公式softmax+Q-function构造了一个概率分布。

6. TIP: Experience Replay

构建Replay Buffer用于经验回放，里边存储的是一系列s,a,r,s序列。

• Replay Buffer中的experience可能来自不同的policy。

• Buffer装满了以后，会将旧的资料丢掉。

• 训练Q-function的时候，会随机从buffer中sample一个batch出来，用这些experience来更新Q-function。

• 这样就是off-policy的方法了，能够高效利用experience，不用重复与环境做互动，效率更高。

• 采用sample数据的方法训练critic可以避免同一个batch中的data都是相似的，希望一个batch data具有多样性。

7. DQN

Deep Q-Network 算法伪代码如下：

• Target Q-function $\hat{Q}$就是上边提到的需要固定的Q-Network, Q是待学习的Q-function。
• 环境的探索使用Epsilon Greedy方法，然后将探索得到的（s,a,r,s）存储到Buffer中供使用。
• 从buffer中sample一个batch，然后回归Target、更新参数。
• 每过C步将Q的参数复制到$\hat{Q}$上。
• DQN和Q-Learning非常相似，不同点在于：
  • DQN 将 Q-learning 与深度学习结合，用深度网络来近似动作价值函数，而 Q-learning 则是采用表格存储；
  • DQN 采用了经验回放的训练方法，从历史数据中随机采样，而 Q-learning 直接采用下一个状态的数据进行学习。

7.1. Double DQN

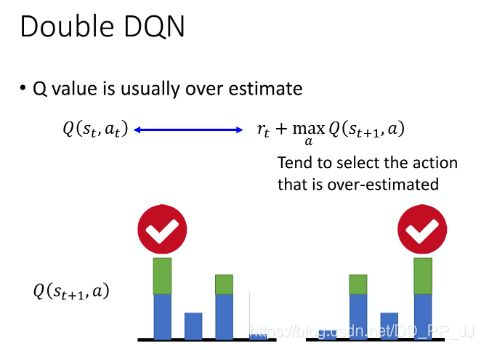
DQN存在一个问题，就是Q-value是被高估的，如上图所示，红色的曲线是DQN的Value， 红色的横线是实际的Value值。

问：为何被高估？

答：DQN的target值容易被设置的过高，因为它总是偏向去取Q-table中最大值。上图中绿色的是被高估的量，被高估以后target就会选择这个action，在此基础上再加上$r_t$作为target value，所以整个过程都是趋向于高估target的。

Double DQN就是为了解决防止估值过高的问题，来看看是怎么做的。

引入两个的Q-network，第一个 Q-network，决定哪一个 action 的 Q value 最大。你用第一个 Q-network 去带入所有的 a，去看看哪一个 Q value 最大。

这种方法如何避免被高估的问题呢：

假设第一个 Q-function 高估了它现在选出来的 action a，那没关系，只要第二个 Q-function $Q^{\prime }$ 没有高估这个 action a 的值，那你算出来的就还是正常的值。

假设反过来是 $Q^{\prime }$ 高估了某一个 action 的值，那也没差， 因为反正只要前面这个 Q 不要选那个 action 出来就没事了。

通俗理解就是，两个人一起做商量着决定往往要比一个人武断决定要好很多。类似行政和立法是分立的，相互制约。

Q:哪里来的两个Q-Network呢？

A: 一个是 target 的 Q-network，一个是真正你会 update 的 Q-network。在 Double DQN 里面，会拿 update 参数的那个 Q-network 去选 action，然后拿 target 的network，那个固定住不动的 network 去算 value。而 Double DQN 相较于原来的 DQN 的更改是最少的，它几乎没有增加任何的运算量，连新的 network 都不用，因为原来就有两个 network 了。

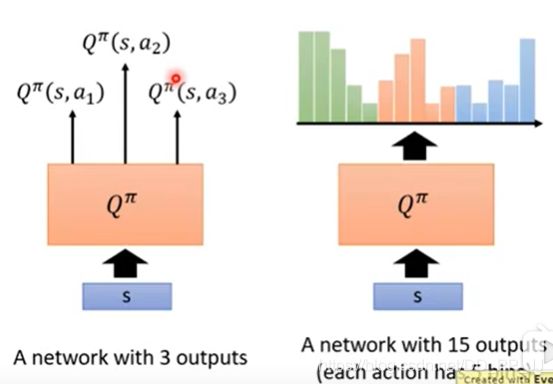
7.2 Dueling DQN

这个也很简单，改了一下模型的结构而已，不直接output Q value 的值，它分成两条 path 去运算，第一个 path 算出一个 scalar，这个 scalar 我们叫做 $V(s)$。因为它跟input s 是有关系，所以叫做 $V(s)$，$V(s)$ 是一个 scalar。下面这个会 output 一个 vector，这个 vector 叫做 $A(s,a)$。下面这个 vector，它是每一个 action 都有一个 value。然后你再把这两个东西加起来，就得到你的 Q value。

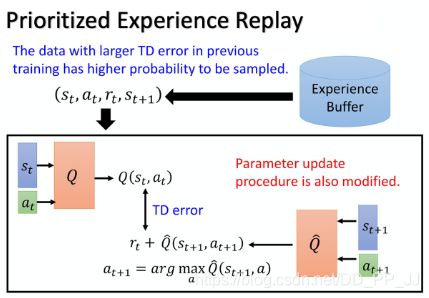
7.3. Prioritized Experience Replay

这是一个从buffer中sample experience的技巧，因为buffer中并不是所有data都是平等的，有的data比较重要。比如有的数据的TD error特别大，说明这种data难度很大，那最好给他更高的概率被sample到，给予它更高的优先级priority。

实际上在做 prioritized experience replay 的时候，不仅会更改 sampling 的 process，还会因为更改了 sampling 的 process，更改 update 参数的方法。所以 prioritized experience replay 不仅改变了 sample data 的 distribution，还改变了 training process。

7.4 Balance between MC and TD

MC 跟 TD 的方法各自有各自的优劣，怎么在 MC 跟 TD 里面取得一个平衡呢？

• 在 TD 里面，在某一个 state $s_t$ 采取某一个 action $a_t$ 得到 reward $r_t$，接下来跳到那一个 state $s_{t+1}$。但是可以不要只存一个 step 的data，我们存 N 个 step 的 data。
• 记录在 $s_t$ 采取 $a_t$，得到 $r_t$，会跳到什么样 $s_t$。一直纪录到在第 N 个 step 以后，在 $s_{t+N}$采取 $a_{t+N}$得到 reward $r_{t+N}$，跳到 $s_{t+N+1}$ 的这个经验，都存下来。
• 要算 target value 的话，要再加上 multi-step 的 reward ${\sum }_{t^{\prime }=t}^{t+N}{r}_{t^{\prime }}$ ，multi-step 的 reward 是从时间 t 一直到 t+N 的 N 个reward 的和。然后希望 $Q(s_t,a_t)$ 和 target value 越接近越好。

7.5. Noisy NET

之前讲的 Epsilon Greedy 这样的 exploration 是在 action 的 space 上面加 noise; 有另外一个更好的方法叫做Noisy Net，它是在参数的 space 上面加 noise。

Noisy Net 的意思是说，每一次在一个 episode 开始的时候，要跟环境互动的时候，就把 Q-function 拿出来，在 network 的每一个参数上面加上一个 Gaussian noise，把原来的 Q-function 变成$\tilde{Q}$ （代表一个Noisy Q-function）。接下来用这个固定住的 noisy network 去玩这个游戏，直到游戏结束，才重新 sample 新的 noise。

Noise on Action 相当于以随机的概率胡乱采取action，并不符合真实的策略。

Noise on Parameters 在权重层面添加noisy，这样遇见了相似的状态的时候，可能依然会采取相同的策略，这就是基于状态的探索。

7.6 Distributional Q-Function

由于Q是一个均值，由很多值平均得到。上图中左右两边的均值是一样的，但是每个值的分布是不同的，比如左边的reward概率都集中在0附近。这个信息在传统的Q-learning方法中就被忽视掉了。

上图左侧是传统Q-learning，右侧是Distributional Q-function，每个action拆成5个bin，直接预测在某一个bin中的概率，根据bin所属action选取action。

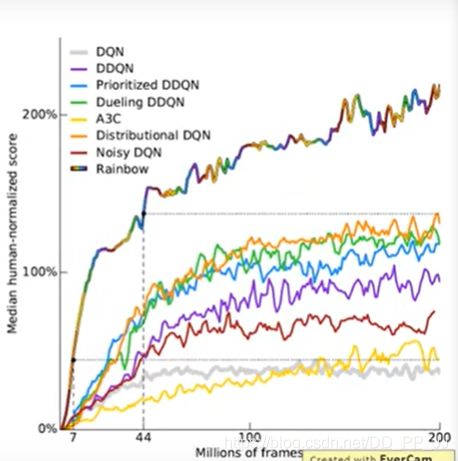
7.7 Rainbow

综合以上所有方法，组成了彩虹。

8. Continuous Actions

https://www.bilibili.com/video/BV1MW411w79n?p=5

Q-learning相比于Policy Gradient很好训练，Policy Gradient一旦遇到状态比较多的，就很难继续训练下去了。但是Q-learning存在的最大的问题就是无法很好的解决action space为连续的情况。
$$a=argma{x}_{a}Q(s,a)$$
Q-learning中策略主要依赖以上公式，以上公式必须要满足action是discrete的条件。那有什么解决办法呢？

Solution 1

Sample 更多的action，用尽可能多的action逼近连续action space。这种方法效率很低，并且不够精确。

Solution 2

**使用Graident Ascent方法来解决这个优化问题。**既然是optimization的问题，可以用gradient ascent, 将a作为parameter，找一个a可以maximize的Q-function。缺点是运算量很大，并且不见得能找到这个optimal的结果。

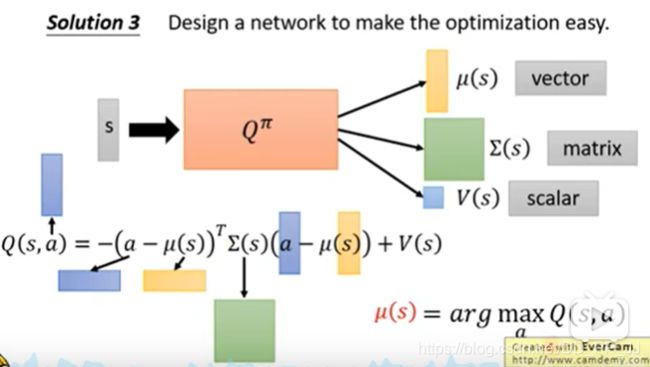
Solution 3

专门设计一个network网络架构，设计Q-function，让求解arg max的问题便容易。

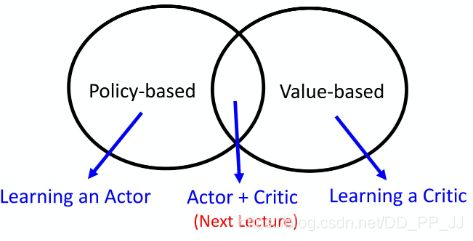
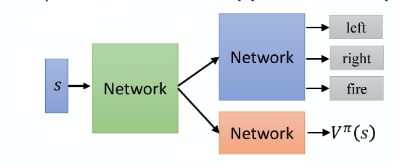
9. Actor-Critic

Actor-Critic是集合了两者的优点而设计出来的，先进行Policy Gradient的Review:

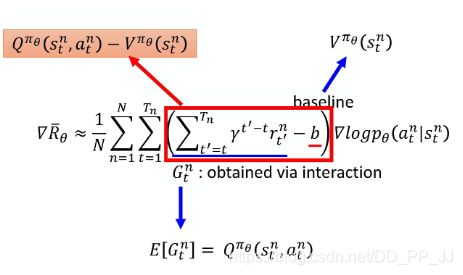
$G_t^n$ 集合了从当前状态到最终的全部reward，是一个random variable，由于累积多个random variable，所以存在很大的不确定性，非常不稳定，如上图所示。如何更好得估测这个$G_t^n$呢?

• 引入State value Function $V^{\pi }$
• 引入State-action Value Function $Q^{\pi }(s,a)$

两者都可以更准确、更好的依据当前状态判断未来可以得到的reward期望值。两者的估计可以用TD（训练比较稳）或者 MC（结果更加精确）

Actor-critic通过引入以上两个状态函数，就可以将Policy Gradient改成以上的样子。

实现的时候，如果按照以上公式准备，那就需要两个network,分别学习Q函数和V函数。两个network可能会带来的不确定的风险，所以能不能只用一个network呢？

有以下公式：
$$Q^{\pi }\left(s_t^n,a_t^n\right)=r_t^n+V^{\pi }\left(s_{t+1}^n\right)$$
带入公式：
$$Q^{{\pi }_{\theta }}\left(s_t^n,a_t^n\right)-V^{{\pi }_{\theta }}\left(s_t^n\right)$$
得到：
$$r_t^n+V^{\pi }\left(s_{t+1}^n\right)-V^{\pi }\left(s_t^n\right)$$
这就是Advantage Function，A2C的整个流程如下图所示：

A2C的小TIP：

• actor $\pi (s)$和critic $V^{\pi }(s)$的参数是共享的。

  

• exploration机制，对 $\pi$ 的 output 的 distribution 进行约束。这个约束是希望这个 distribution 的 entropy不要太小，希望不同的 action 它的被采用的机率，平均一点。这样在测试的时候，才会多尝试各种不同的 action，才能更充分探索环境。

Question: 在讲解TD 估计V的时候存在以下公式：
$$V^{\pi }\left(s_t\right)=V^{\pi }\left(s_{t+1}\right)+r_t$$

那将这个公式带入：
$$r_t^n+V^{\pi }\left(s_{t+1}^n\right)-V^{\pi }\left(s_t^n\right)$$
直接0，这个如何解释？

Answer: @来自助教江季&老板

主要是TD那个公式，上边讲解TD公式的时候，其实表达并不严谨，只是为了方便读者理解，严谨的表达式如下：
$$V(S_t)\leftarrow E_{\pi }[R_{t+1}+\gamma V(S_{t+1})]$$

TD中使用的蒙特卡洛估计来计算Value函数的值，而在A2C中，使用的是网络进行估计的值，所以不满足等式：$V^{\pi }\left(s_t\right)=V^{\pi }\left(s_{t+1}\right)+r_t$

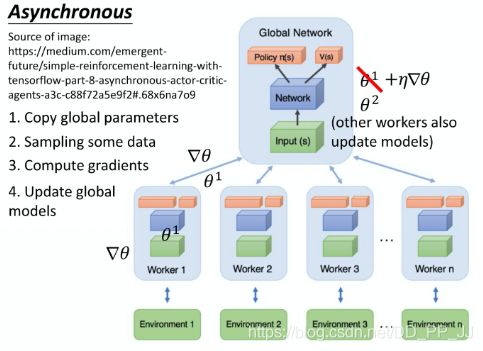
10. Asynchronous Advantage Actor-Critic(A3C)

A2C缺点是训练太慢，如何改进呢？引入分布式的方法，多个agent同时训练。

每个线程都负责一个agent，去跟环境做交互。具体过程如下：

• 线程copy global Network的参数，复制一份。
• 采样一些数据experience进行学习
• 计算梯度
• 将梯度更新到global network.

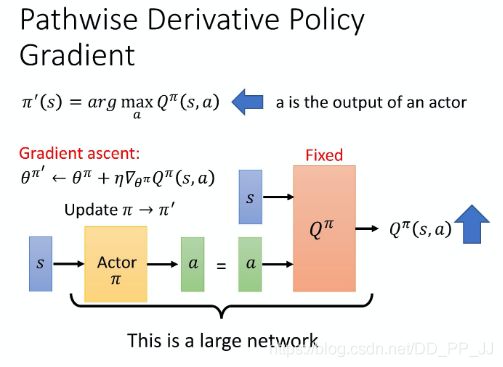
11. Pathwise Derivative Policy Gradient

这是一种Q-learning解决continuous action space的方法，可以看作一个特别的actor-critic。

如何解这个optimization问题？用一个actor来求解。假设actor就是一个solver，其工作就是给出state s以后，求解哪一个a能带来最大的Q value。

和GAN进行对比：

	GAN	A3C
生成	generator	Actor
评判	discriminator	Critic

• 对原来的Q-learning进行改进，learn一个actor，用于求解argmax的问题，也就是上述的solution 3
• 原来的actor-critic中，critic并没有给actor足够多的信息，只告诉其好或者不好，没有指导。现在的新方法直接告诉actor什么action才是更好的。

具体的算法：

算法流程：

Q-learning algorithm:

Q-learning改成Pathwise Derivative Policy Gradient方法：

AC和GAN之间的联系：

GAN和AC都是以难训练出名的，这两者可以互相借鉴一些训练的思路和解决方案。

12. 补充

为什么在DQN中采用价值函数近似（Value Function Approximation）的表示方法？

答：首先DQN为基于深度学习的Q-learning算法，而在Q-learning中，我们使用表格来存储每一个state下action的reward，即我们前面所讲的状态-动作值函数 $Q(s,a)$ 。但是在我们的实际任务中，状态量通常数量巨大并且在连续的任务中，会遇到维度灾难的问题，所以使用真正的Value Function通常是不切实际的，所以使用了价值函数近似（Value Function Approximation）的表示方法。