入门系列之改进小波阈值降噪

1. 小波阈值降噪特点

        近年来，小波理论得到了非常迅速的发展，而且由于其具备良好的时频特性，因而实际应用也非常广泛。在去噪领域中，小波理论也同样受到了许多学者的重视，并获得了比较好的效果。

        小波去噪方法的成功主要得益于小波变换具有如下特点:

        (1) 多分辨率，由于采用了多分辨率的方法，所以可以非常好地刻画信号的非平稳特征，如边缘、尖峰、断点等；

        (2) 去相关性，因为小波变换可以对信号进行去相关，且噪声在变换后有白化趋势，所以小波域比时域更利于去噪；

        (3) 选基灵活性，由于小波变换可以灵活选择变换基，从而对不同应用场合，对不同的研究对象，可以选用不同的小波母函数，以获得最佳的效果。

2. 小波阈值降噪概念与步骤

2.1 小波分解概念

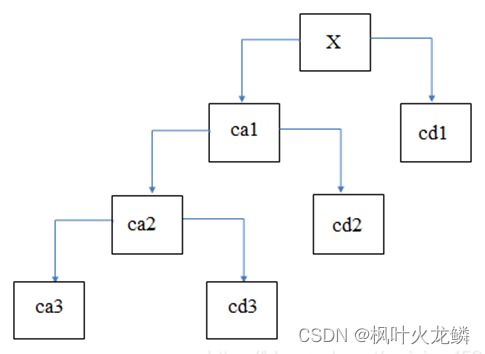
        小波分解使用Mallat塔式算法对信号进行降阶分解。该算法在每尺度下将信号分解成低频近似分量（CA）与高频细节分量（CD），以3层小波分解为例，其分解树如图1所示。而噪声能量主要是集中在小波分解的细节分量中。

​ 图1 3层小波分解树

2.2 小波阈值降噪步骤

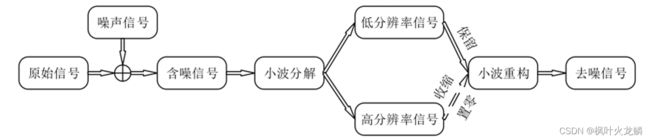
        针对噪声能量主要是集中在小波分解的细节分量，小波阈值去噪过程主要分为三步：

        (1) 小波分解过程，即选定一种小波基函数对信号进行n层小波分解；

        (2) 阈值处理过程，即对分解得到的各层细节分量系数进行阈值处理，获得估计小波系数；

        (3) 重构过程，对处理后的小波系数进行小波逆变换，从而获得去噪后的信号。

        下图为小波阈值降噪流程图。

图2 小波阈值降噪流程图

 

3. 改进的阈值确定与阈值函数

        在小波域中，有效信号对应的系数很大，而噪声对应的系数很小并且仍满足高斯分布。因此可以通过确定阈值和阈值处理函数，将信号在小波域某段区间内的系数按阈值函数的定义，进行一定的收缩、置零等变换，从而实现抑制噪声的目的。

3.1 阈值的确定

        目前常见的阈值确定方法主要有：无偏风险估计阈值、极大极小阈值、固定阈值、启发式阈值等，MATLAB自带的自适应阈值选择函数为 thselect 。改进的阈值确定方法与阈值函数参考的是文献 [3]。

3.2 阈值函数

        在确定了高斯白噪声在小波域的阈值门限之后，就需要有个阈值函数对含有噪声系数的小波系数进行过滤，去除高斯噪声系数，常用的阈值函数有硬阈值和软阈值函数两种。

        但硬阈值法降噪得到重构的信号方差较大，并存在振荡现象，信号平滑性较差；而软阈值法降噪最终得到的信号与原始含噪信号之间存在恒定偏差。针对上述的这些问题，专家学者们提出了许多性能更好的阈值函数，而图3则是文献[3]提出的改进阈值函数与传统的软、硬阈值函数的对比图。

图3 阈值函数对比

 

4. 降噪效果可视化与评估

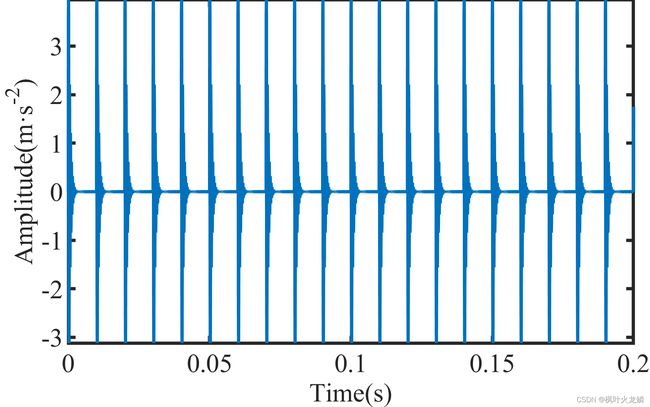
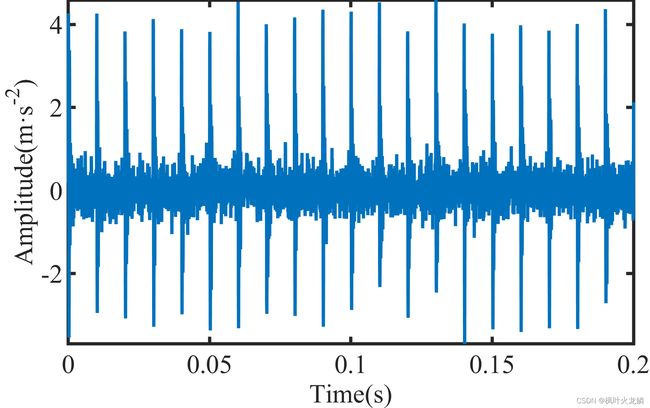
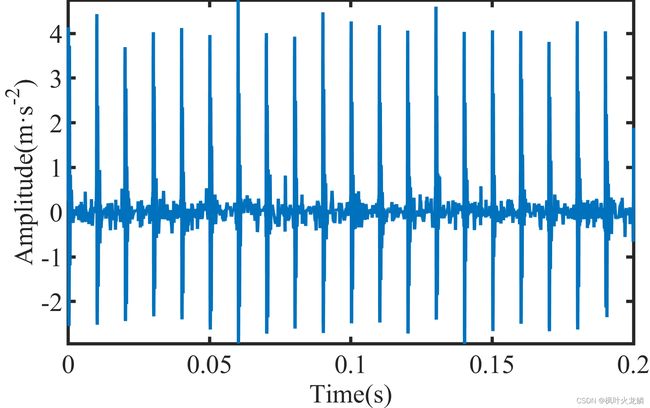
        本文仿真信号为一轴承外圈故障的振动信号，加入的噪声大小为 5DB，其中原始和加噪后的信号如图4、5所示。

图4 原始信号

 

图5 加噪信号

 采用改进阈值降噪算法对含噪信号进行降噪，最终的效果如图6所示。

图6 降噪后信号

         为了验证算法的降噪性能，本文采用了输出信噪比（Signal-noise ratio, SNR）、均方误差 （Root-mean-square error, RMSE）以及平滑度（r）作为衡量标准来检验改进算法的降噪效果，具体数值如下所示。

5. 参考视频

[1] 入门系列之改进小波阈值降噪_哔哩哔哩_bilibili

6. 参考文献

[1] 小波去噪_百度百科 (baidu.com)

[2] (10条消息) 小波阈值去噪_Zhi Zhao的博客-CSDN博客_小波阈值去噪

[3] 徐博, 刘斌, 刘德政, 等. 基于小波理论的舰船 IMU 加速度计信号处理算法[J]. 中国舰船研究, 2020, 15(2): 151-158,164.