论文笔记:WWW 2020 Heterogeneous Graph Transformer
1. 前言
论文链接:https://arxiv.org/abs/2003.01332
github:https://github.com/acbull/pyHGT
近年来,图神经网络(GNNs)在结构化数据建模方面取得了巨大的成功。但是,大多数GNN为同构图设计,同构图中所有的节点和边都属于相同的类型,这使得它们无法表示异构结构。本文中提出了一种异构图转换器(HGT)体系结构来建模网络规模的异构图。为了对异质性进行建模,本文设计了节点和边类型相关的参数来表征每个边缘上的异质性注意,使HGT能够对不同类型的节点和边缘保持专门的表示。
- 为了处理动态异构图,本文在HGT中引入了相对时间编码技术,能够捕获任意持续时间下的动态结构依赖关系。
- 为了处理web规模的图数据,本文设计了异构的小批量图采样算法hgsampling来进行高效和可扩展的训练。
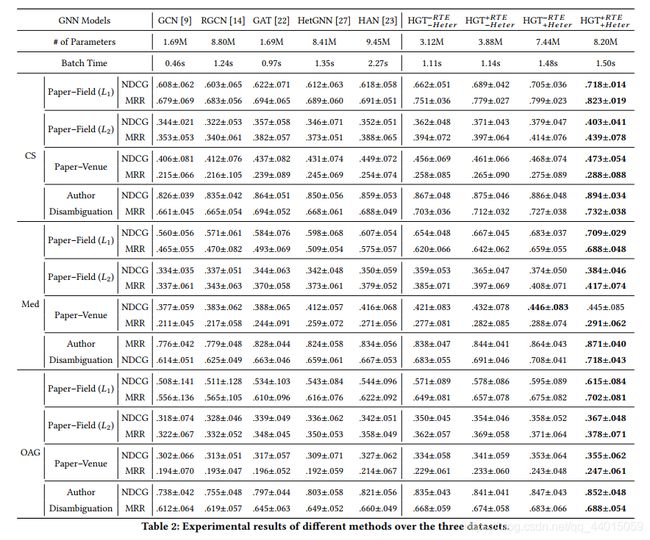
在拥有1.79亿个节点和20亿个边的开放学术图上进行的大量实验表明,在各种下游任务上,提出的HGT模型始终比所有最先进的GNN基线性能高出9%-21%。
2. 异质图
本文中进行实验的主要对象为 Open Academic Graph (OAG)
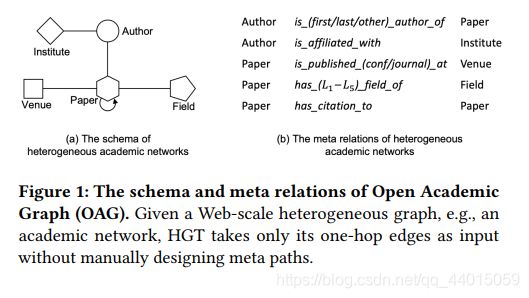
其中包含了五类节点,分别为:论文、作者、机构、场所(期刊、会议或预印本)和字段,以及它们之间的不同类型的关系。
在过去的十年中,已经有一些研究工作致力于探索挖掘异质图。经典的范例之一是定义和使用元路径来建模异构结构,例如PathSim和metapath2vec。近年来,鉴于graph neural networks (GNNs)的成功,有几次尝试采用GNNs对异构网络进行学习。但是这些工作面临着几个问题:
- 首先,大部分涉及到对每种异构图类型的元路径的设计,需要特定的领域知识(人工手动定义);
- 其次,它们要么简单假设不同类型的节点/边共享相同的特征和表示空间,要么单独对节点类型或边类型保持不同的非共享权值,不足以捕获异构图的属性;
- 第三,大部分忽略了每个(异质)图的动态特性;最后,它们内在的设计和实现使它们无法建模大规模的异构图。
以OAG为例:首先,OAG中的节点和边缘可以具有不同的特征分布,如论文具有文本特征,机构可能具有附属学者的特征,合作作者与引文链接之间存在明显差异;其次,OAG一直在不断发展,例如,
- 1)出版物的数量每12年翻一番
- 2)KDD会议在20世纪90年代更多地与数据库相关,而近年来更多地与机器学习相关;
- 3)最后,OAG包含数亿个节点和数以亿计的关系,使得现有的异构GNN方法无法进行扩展处理。
鉴于这些局限性和挑战,首先明确基于图神经网络来挖掘异质图特征的几个要点:
- 异构图神经网络的目标是维护依赖于节点和边缘类型的表示,捕获网络动态,避免自定义元路径,并可扩展到网络规模的图。在此工作中,我们提出了异构图转换器(HGT)架构来处理这些问题。为了处理图的异构性,引入了节点依赖注意机制和边依赖注意机制。相较于其他方法选择参数化每种类型的边缘,本文选择通过对每条边进行分解,定义了HGT中的异质相互注意机制 e = ( s , t ) e = (s, t) e=(s,t) ,此种方式是基于其原路径关系的元组关系,也就是说,<节点类型的 s s s,在 t t t 类型节点之间的边的种类 e e e> 的节点类型。
图1展示了异质学术图的元关系。具体来说,我们使用这些元组关系来参数化权重矩阵,以便计算每条边上的注意力。因此,允许不同类型的节点和边维护它们的特定表示空间。与此同时,不同类型的连接节点仍然可以交互、传递和聚合消息,而不受其分布差距的限制。由于其体系结构的本质,HGT可以通过跨层的消息传递来合并来自不同类型的高阶邻居的信息,这可以被视为“软”元路径。
也就是说,即使HGT只使用它的单跳边缘作为输入,而无需人工设计元路径,所提出的注意力机制也可以自动地、隐式地学习和提取对不同下游任务重要的“元路径”。以元组的关系模式来替代元路径形成“软”元路径 - 为了处理图动态,本文提出了相对时间编码(RTE)策略来增强HGT。该方法没有将输入图分割成不同的时间戳,而是将所有发生在不同时间的边作为一个整体来维护,并设计RTE策略来建模具有任意持续时间长度的结构化时间依赖关系,甚至是不可见的和未来的时间戳。RTE通过端到端训练,使HGT能够自动学习异构图的时间依赖性和演化。
- 为了处理大规模的图数据,本文设计了第一个异构子图采样算法 HGSampling—for minibatch GNN training。其主要思想是对不同类型节点比例相似的异构子图进行采样,因为直接使用现有的(同构的)GNN采样方法,如GraphSage、FastGCN和LADIES,会导致节点和边类型的高度不平衡。此外,还该异质图采样方法还保持采样子图密集,以尽量减少信息损失。使用HGSampling,所有的GNN模型,包括本文提出的HGT,都可以在任意大小的异构图上进行训练和推断。
本文演示了提出的异构图转换器在网络规模的开放学术图上的有效性和效率,该开放学术图包含1.79亿个节点和20亿个边,时间跨度从1900年到2019年,这是迄今为止在异构图上执行的规模最大、跨越时间最长的表示学习。此外还研究了特定领域的图:计算机科学和医学学术图。实验结果表明,HGT可以显著改善各种下游任务在最先进的GNNs和专用的异构模型9-21%。
3. 相关工作
3.1 元路径
为了更好地模拟真实世界的异构网络,本文假设在不同类型的节点之间可能存在多种类型的关系。例如,在OAG中,考虑作者顺序,作者与论文节点之间存在不同类型的关系,如“第一作者”、“第二作者”等。
3.2 动态异质图
为了模拟真实世界(异构)图的动态本质,当节点 s s s 在 T T T 时刻连接到节点 t t t 时,赋予边 e = ( s , t ) e = (s, t) e=(s,t) 一个时间戳 T T T,。如果 s s s 第一次出现, T T T 也被分配给 s s s 。随着时间的推移建立连接,那么 s s s 可以与多个时间戳相关联。
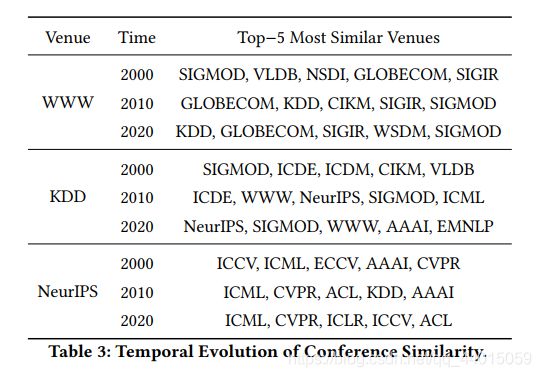
换句话说,假设一条边的时间戳是不变的,边的时间戳表示它被创建的时间。例如,当一篇论文在时间 T T T 在一个会议上发表时, T T T 将被分配到论文和会议节点之间的边。相反,可以为节点相应地分配不同的时间戳。例如,会议节点“WWW”可以在任何一年分配。WWW @1994意味着我们正在考虑的是第一版WWW,它更关注互联网协议和Web基础设施,而WWW @2020意味着即将到来的WWW,它将其研究主题扩展到社会分析、无处不在的计算、搜索和IR、隐私和社会等。
异构图挖掘的研究已经有了重要的进展,如节点分类、聚类、排序和表示学习[3,17 - 19],而动态视角关于HGs的研究还没有得到广泛的探索和研究。
3.3 一般化的GNN架构
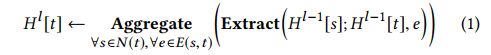
H l [ t ] H^l[t] Hl[t]代表GNN 中第 l l l 层节点 t t t 的节点表示, s s s 代表与节点 t t t 相关的节点集合, E ( s , t ) E(s,t) E(s,t) 代表节点之间的边的关系
其中最重要的GNN操作是 E x t r a c t ( ⋅ ) Extract(\cdot) Extract(⋅) 和 A g g r e g a t e ( ⋅ ) Aggregate(\cdot) Aggregate(⋅),分别代表邻居信息提取器和信息聚合器。其中信息聚合器简单的可以采用一些均值,加和或最大值操作,还可以设计更复杂的池和规范化函数
3.4 异质GNNs
最近,一些研究试图扩展GNNs来建模异构图。
- 关系图卷积网络(RGCN)建模知识图。RGCN为每条边类型保留不同的线性投影权值。
- 异构图神经网络(HetGNN),它对不同的节点类型采用不同的神经网络(RNNs)来集成多模态特征。
- HAN 通过对不同元路径定义的边保持不同的权值来扩展图注意力网络。它们还使用高级语义注意来区分和聚合来自不同元路径的信息。
虽然这些方法在经验上优于传统的GCN和GAT模型,但它们并没有充分利用异构图的特性。它们都单独使用节点类型或边类型来确定GNN权值矩阵。然而,不同类型的节点或边计数可能会有很大差异。对于那些没有充分出现的关系,很难了解准确的关系特定权重。
为了解决这个问题,我们建议考虑参数共享,以便更好地泛化。给定一个边 e = ( s , t ) e = (s, t) e=(s,t) 与元关系 ⟨ τ ( s ) , ϕ ( e ) , τ ( t ) ⟩ ⟨τ(s),ϕ(e),τ(t)⟩ ⟨τ(s),ϕ(e),τ(t)⟩,如果我们使用三个交互矩阵模型相对应的三个元素 τ ( s ) , ϕ ( e ) τ(s),ϕ(e) τ(s),ϕ(e) 和 τ ( t ) τ(t) τ(t) 的元关系,然后大部分的权重可以共享。
例如,在“第一作者”和“第二作者”关系中,他们的源节点和目标节点类型分别都是要写论文的作者。换句话说,从一个关系中学习到的关于作者和论文的知识可以迅速转移和适应另一个关系。因此,我们将此思想与强大的变压器式注意力架构相结合,提出了异构图形转换器。
总结本文创新点如下:
-
(1)避免单独使用节点类型或边类型来确定GNN权值矩阵,本文提出使用元关系 ⟨ τ ( s ) , ϕ ( e ) , τ ( t ) ⟩ ⟨τ(s),ϕ(e),τ(t)⟩ ⟨τ(s),ϕ(e),τ(t)⟩ 分解的相互作用和转换矩阵,使HGT高度捕捉共同和不同的特定模式使用相同或更少参数的关系。
-
(2)与目前大多数基于自定义元路径的工作不同,本文依靠神经结构的本质来整合高阶异构邻居信息,从而自动学习隐式元路径的重要性。
-
(3)以往的研究大多没有考虑(异构)图的动态特性,而本文提出了相对时间编码技术,利用有限的计算资源来整合时间信息。
-
(4)现有的异构GNN都不是针对大图设计和实验的,因此本文提出了大图训练设计的异构小批量图采样算法,可以在10亿尺度的开放学术图上进行实验。
4. HGT
异构图转换器(HGT)。其思想是利用异构图的元关系来参数化权重矩阵(避免利用单独的节点类型或者边类型来确定GNN权值矩阵),用于异构的相互关注、消息传递和传播步骤。并为了进一步整合网络动态,在模型中引入了一个相对的时间编码机制。
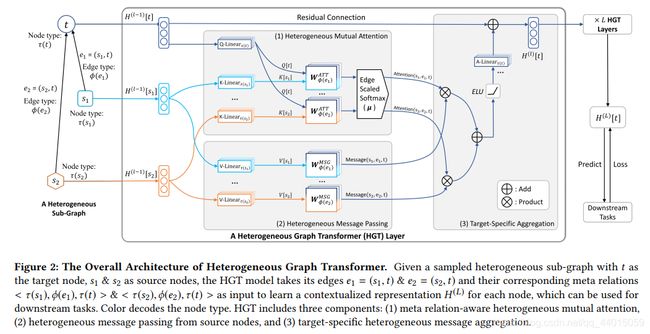
4.1 Overall HGT Architecture
图2展示了异构图转换器的总体架构。给定一个采样异构子图。高度提取所有链接的节点对,目标节点 t t t 是由源节点 s s s 通过边 e e e 所连接的对象。HGT的目标是从源节点聚合信息得到更符合实际的目标节点表示 t t t 。这种过程可以分解为三个组件:
- 异构相互关注(Heterogeneous Mutual Attention) - -针对于源节点和目标节点的注意力表示
- 异构的消息传递(Heterogeneous Message Passing)- - 针对于源节点
- 有针对性的聚合(Target-Specific Aggregation) - - 上述两个模块的有针对性聚合
将第 l l l 层的输出表示为 H ( l ) H^{(l)} H(l),它也是第 l l l 层的输入。通过叠加 L L L 层,我们可以得到整个图的节点表示 H ( L ) H^{(L)} H(L),可以用于端到端训练或馈入下游任务。
4.2 Heterogeneous Mutual Attention
第一步是计算在源节点和目的节点之间的相互注意力,可以用如下的形式来表示:

其中包含了三个主要的操作函数,分别是 A t t e n t i o n Attention Attention 来估计每个源节点的重要性、 M e s s a g e Message Message 仅通过源节点 s s s 来提取信息、 A g g r e g a t e Aggregate Aggregate 根据注意力权重来聚合邻居信息。对于普通图注意力方法 GAT 来说,其中的三个模块可以表示为:
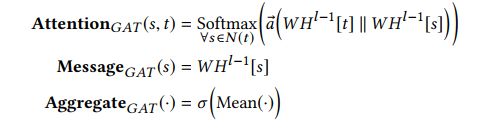
上述方法不能直接用于异质网络中的原因在于,GAT在同质图中默认节点 s s s 和 t t t 的特征分布相同,因此采用权重共享的策略,但是在异质图中,每个点的可能代表不同的含义,这导致点的特征分布在不同空间中,因此为了解决传统同质图 GAT 方法的局限性,本文提出了 Heterogeneous Mutual Attention。给出一个目标节点 t t t ,他的所有邻居为 s ∈ N ( t ) s \in N(t) s∈N(t) ,他们可能用于不同的特征分布(属于不同类的节点),我们希望可以基于元关系 < T ( s ) , ϕ ( e ) , T ( t ) > <\mathcal{T(s),\phi(e),T(t)}> <T(s),ϕ(e),T(t)> 来计算它们的相互注意力。
作者收到 NLP 领域中 Transformer 结构的启发,将目标节点 t t t 映射成为查询向量(Query vector),将源节点认为是 Key向量,将它们的点积结果当作是注意力。关键的区别是,普通的Transformer对所有单词使用一组投影,而在异质图中,每个元关系应该有一组不同的投影权重。为了使参数共享最大化,同时保持不同关系的具体特征,文中提出将交互算子的权矩阵参数化为源节点投影、边缘投影和目标节点投影。具体来说,通过以下方法计算每条边的 e = ( s , t ) e = (s,t) e=(s,t) 的 h-head attention(图2 (1)):
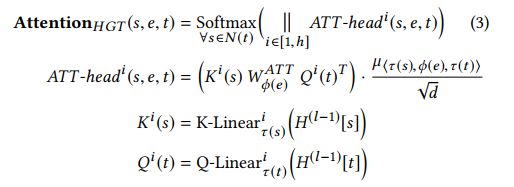
首先,对于第 i i i 个注意头 A T T − h e a d i ( s , e , t ) ATT -head^i(s,e,t) ATT−headi(s,e,t),采用线性投影 K − L i n e a r T ( s ) i : R d → R d h K-Linear^i_{\mathcal{T}(s)}: \mathbb{R}^d→\mathbb{R}^{\frac{d}{h}} K−LinearT(s)i:Rd→Rhd,其中 h h h 为注意头的个数、 d h \frac{d}{h} hd是每个头的矢量维数。每种类型的节点都有一个唯一的线性投影来最大限度地模拟分布差异。类似地,使用线性投影 Q − L i n e a r T ( t ) i Q-Linear^i_{\mathcal{T}_{(t)}} Q−LinearT(t)i将目标节点 t t t 投影到第 i i i 个查询向量中。
并且由于每条元路径的信息的差异性,因此引入一个独特的基于边的矩阵 W ϕ ( e ) A T T ∈ R d h × d h W_{\phi(e)}^{ATT} \in \mathbb{R}^{\frac{d}{h}\times\frac{d}{h}} Wϕ(e)ATT∈Rhd×hd
此外,由于并非所有的关系对目标节点的贡献都是相等的,我们添加一个先验张量 μ ∈ R ∣ A ∣ × ∣ R ∣ × ∣ A ∣ \mu \in \mathbb{R}^{| \mathcal{A} |\times|\mathcal{R} |\times| \mathcal{A}|} μ∈R∣A∣×∣R∣×∣A∣ 来表示每个元关系三元组的一般意义,作为对注意力的自适应缩放。最后,将 h h h 个注意力头连接在一起,得到每个节点对的注意力向量。然后,为每个目标节点,我们从邻居 N ( t ) N(t) N(t) 收集所有注意力向量,计算softmax正则化,使其满足 ∑ ∀ s ∈ N ( t ) A t t e n t i o n H G T ( s 、 e 、 t ) = 1 h × 1 \sum_{∀s∈N (t)} Attention_{HGT}(s、e、t) = 1_{h×1} ∑∀s∈N(t)AttentionHGT(s、e、t)=1h×1。
4.3 Heterogeneous Message Passing
在计算相互关注的同时,我们将信息从源节点传递给目标节点(见图2(2))。与注意过程类似,希望将边的元关系合并到消息传递过程中,以缓解不同类型节点和边缘的分布差异。对于一对节点 e = ( s , t ) e = (s, t) e=(s,t),通过:
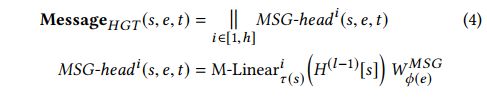
来获得第 i i i 层的信息头 M S G − h e a d i ( s , e , t ) MSG-head^i(s,e,t) MSG−headi(s,e,t)。
首先对于不同类型的节点先进性特征空间的转换 M − L i n e a r T ( s ) i : R d → R d h M-Linear_{\mathcal{T}(s)}^i:\mathbb{R}^d \rightarrow\mathbb{R}^{\frac{d}{h}} M−LinearT(s)i:Rd→Rhd。之后接一个元路径信息的影响权重 W ϕ ( e ) M S G ∈ R d h × d h W_{\phi({e})}^{MSG} \in \mathbb{R}^{\frac{d}{h}\times\frac{d}{h}} Wϕ(e)MSG∈Rhd×hd。最后是一个拼接操作,拼接所有注意力头。
4.4 Target-Specific Aggregation
计算出异构的多头注意力和消息后,我们需要将它们从源节点聚合到目标节点(参见图2(3))。(3)中的softmax 使每个目标节点 t t t 的注意向量之和为1,因此我们可以简单地使用注意向量作为权值,对来自源节点的对应消息进行平均,得到更新后的向量 H ~ ( l ) [ t ] \widetilde{H}^{(l)}[t] H (l)[t]为:
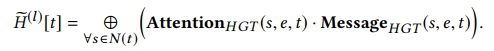
这将从它的不同特性分布的所有邻居(源节点)聚集信息到目标节点 t t t 。最后一步是将目标节点 t t t 的向量映射回其类型特定分布。为此对更新后的向量 H ~ ( l ) [ t ] \widetilde{H}^{(l)}[t] H (l)[t] 进行线性投影 A − L i n e a r T ( t ) A - Linear_{\mathcal{T}(t)} A−LinearT(t),并加上残差链接,最后的表达形式为:
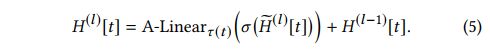
通过这种方式,目标节点 t t t 的第 l l l 层HGT层的输出为 H ( l ) [ t ] H^{(l)}[t] H(l)[t]。由于现实世界的“小世界”特性图,叠加HGT块 l l l 层( l l l是一个小值)可以使每个节点相邻的大部分节点均具有不同的类型和关系。即HGT为每个节点生成高度上下文化的表示 H ( L ) H^{(L)} H(L),可将其输入任何模型,进行下游异构网络任务,如节点分类、链路预测等。
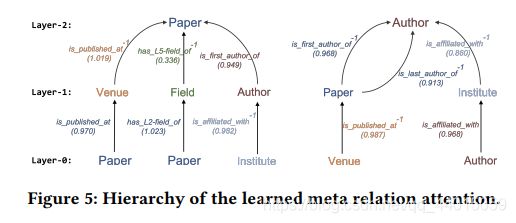
整个模型架构高度依赖使用元关系 ⟨ τ ( s ) , ϕ ( e ) , τ ( t ) ⟩ ⟨τ(s),ϕ(e),τ(t)⟩ ⟨τ(s),ϕ(e),τ(t)⟩——参数化矩阵的权重。这可以解释为模型容量和效率之间的权衡。与普通 Transformer 相比,我们的模型区分了不同关系的算子,从而更能处理异构图的分布差异。与现有的模型相比,保留了HGT的三联体参数化可以更好地利用异构图模式实现参数共享。
- 一方面,较少出现的关系可以从这种参数共享中获益,以实现快速的自适应和泛化。
- 另一方面,不同关系的操作符仍然可以通过使用小得多的参数集来保持其特定的特征。
4.5 Relative Temporal Encoding
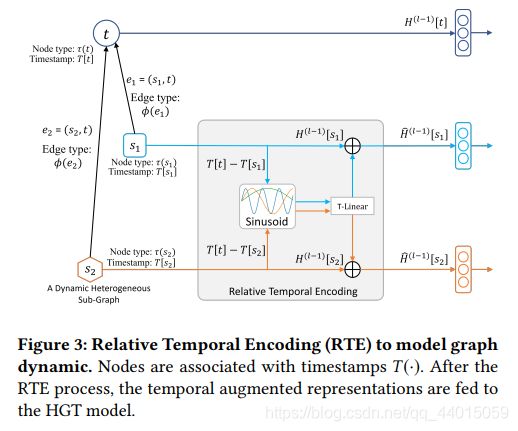
到目前为止,本文提出了HGT-a图神经网络来建模异构图。接下来介绍了相对时间编码(RTE)技术,用于HGT处理图的动态。传统的合并时间信息的方法是为每个时隙构造一个单独的图。然而,这样的过程可能会在不同的时间槽中丢失大量的结构依赖关系。同时, t t t 时刻节点的表示可能依赖于发生在其他时隙的边。因此,对动态图建模的一种正确方法是保持所有发生在不同时间的边,并允许具有不同时间戳的节点和边相互交互。基于此,我们提出了相对时间编码(RTE)机制来建模异构图的动态依赖关系。RTE的灵感来自Transformer的位置编码方法,该方法已被证明能够成功地捕获长文本中单词的顺序依赖关系。具体来说,给定一个源节点 s s s 和一个目标节点 t t t ,以及它们对应的时间戳 T ( s ) T (s) T(s) 和 T ( t ) T (t) T(t),我们将相对时间间隙 ∆ T ( t , s ) = T ( t ) − T ( s ) ∆T (t,s) = T (t)−T (s) ∆T(t,s)=T(t)−T(s) 作为索引,得到相对时间编码 R T E ( ∆ T ( t , s ) ) RTE(∆T (t,s)) RTE(∆T(t,s))。训练数据集不会覆盖所有可能的时间间隔,因此RTE应该能够一般化到未见时间和时间间隔。因此采用一组固定的正弦函数作为基,带有可调线性投影 T-Linear : R d → R d \mathbb{R}^d\rightarrow \mathbb{R}^d Rd→Rd为RTE:
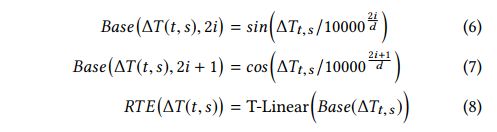
最后,在源节点 s s s 的表示中加入相对于目标节点 t t t 的时间编码,如下所示:
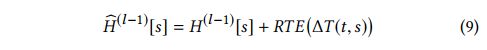
这样,时间增广表示 H ^ ( l − 1 ) \hat{H}^{(l−1)} H^(l−1) 将获取源节点 s s s 和目标节点 t t t 的相对时间信息,RTE过程如图3所示。
5. WEB-SCALE HGT TRAINING
5.1 HGSampling
全批的 GNN 训练需要计算每一层的所有节点表示,这使得它不能用于web规模的图。为了解决这个问题,直接对异构图使用同构图类型数据的采样方法,容易得到对于不同节点类型非常不平衡的子图,因为每种类型的度分布和节点总数可能会有很大差异。为了解决这个问题,本文提出了一种高效的异构小批图采样算法- HGSampling,使HGT和传统的 GNN 都能处理web规模的异构图。HGSampling能够
- 1)保持每种类型的节点和边的数量相近
- 2)保持采样子图的密集性最小化信息损失,降低样本方差。
算法1概述了HGSampling算法。它的基本思想是为每个节点类型 T \mathcal{T} T 保留一个单独的节点预算 B [ T ] B[\mathcal{T}] B[T] [已知节点 t t t 已经采样,用算法2将其所有的直接邻居加到相应的预算中,并在第8行中对这些邻居加上 t t t 的归一化度,用于计算采样概率。这种归一化相当于将每个采样节点的随机游走概率累加到其邻域,避免采样被高度节点所控制。直观地看,该值越高,则候选节点与当前采样节点的关联程度越高,因此应该给予被采样的概率越高。
更新预算后,在算法1第9行中计算抽样概率,其中计算每个预算中每个节点s的累计归一化度的平方。利用这种抽样概率可以降低抽样方差。然后,在第12-15行中,使用计算出的概率对 n n n 个类型的节点进行抽样,将它们添加到输出节点集,更新其邻域到预算,并将其从预算中移除。重复这个过程 L L L 次,得到一个从初始节点开始的深度为 L L L 的采样子图。最后,重构了采样节点间的邻接矩阵。通过使用上述算法,采样后的子图每个类型的节点数量相近(基于单独的节点预算),且足够密集,可以降低采样方差(基于归一化程度和重要性采样),适合在web规模的异构图上训练 GNN。

5.2 Inductive Timestamp Assignment

到目前为止,我们假设每个节点 t t t 都被分配了一个时间戳 T ( t ) T(t) T(t)。然而,在真实的异构图中,许多节点并不与固定的时间相关联。因此,我们需要给它分配不同的时间戳。我们将这些节点表示为普通节点。例如,WWW会议是在1974年和2019年举行的,这两年的WWW节点有着截然不同的研究主题。因此,我们需要决定将哪个时间戳附加到WWW节点上。
在异构图中也存在具有显式时间戳的事件节点。例如,paper节点应该与它的发布行为相关联,从而与它的发布日期相关联。提出了一种基于关联事件节点的归纳时间戳分配算法来分配普通节点的时间戳。算法如算法2第6行所示。其思想是计划节点从事件节点继承时间戳。检查候选源节点是否为事件节点。如果是,就像在特定年份发表的论文一样,保留它的时间戳来捕获时间依赖性。如果没有,比如一个可以与任何时间戳关联的会议,我们将关联节点的时间戳(例如其论文的发表年份)归纳分配给这个普通节点。这样,可以在子图采样过程中自适应地分配时间戳。