第三十五章 数论——卡特兰数

一、什么是卡特兰数

1、推导

我们看下面这个坐标系：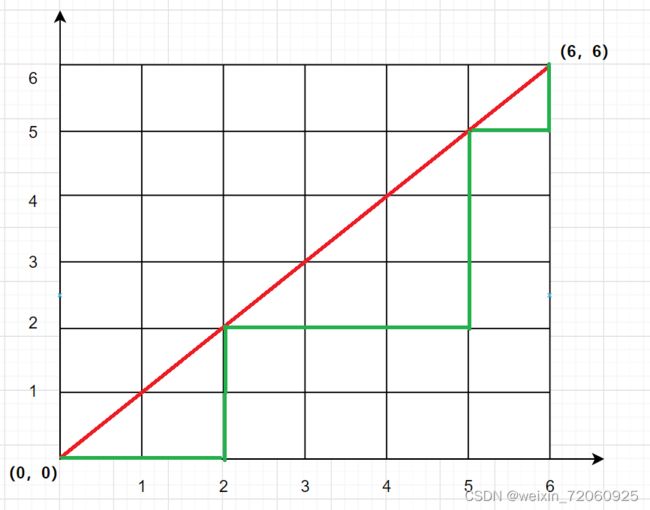
我们从$(0,0)$点到$(6,6)$点的路线有很多，并且根据我们高中排列组合的知识，相当于从12条边中，随机选出6个向上的。所以，在不加任何限制条件的情况下，我们的路线条数为：$C_{12}^6$

但是，我们现在加一个限制条件，我们只允许这个路线在红线的下面，那么现在怎么求呢？

我们可以采用正难则反的思想，用总共的条数减去不符合上述限制的条数，即是我们的结果，那么我们如何求不合法的情况呢？

既然越过了红线，那么必定会经过蓝色的线，由于我们的终点是$(6,6)$，那么此时我们将终点关于蓝色线对称，那么此时终点的对称点就是$(5,7)$，也就是说，我们越界的路线，关于蓝色的对称线，必定是经过$(5,7)$的。也就是说，我们越界的线的条数，等价于到$(5,7)$的线。

那么为什么呢？

我们反过来想，由于对称点在蓝线的上面，所以我们到达对称点的路线必定是越界的，将这些越界的线对称回来后，必定还是有的点在蓝线上，而终点对称到了$(6,6)$，也就是说对称回来的路线符合了到达终点并且越界的情况。所以二者等价。

那么我们这种情况的路线数目就是从12条边中，随机选5条横着的。$C_{12}^5$

所以在红线之下的路线数目就是：$C_{12}^6-C_{12}^5$

一般化的路线数目就是：
$$C_{2n}^n-C_{2n}^{n-1}$$

这个就是卡特兰数。

2、公式

$$C_{2n}^n-C_{2n}^{n-1}=\frac{C_{2n}^n}{n+1}$$

二、卡特兰数的应用

1、问题：

2、分析

这道题我们直接用公式计算就可以了，那么问题的关键在于怎么计算组合数。组合数的计算可以用定义，因为模数是质数，所以我们求逆元的时候可以使用费马小定理。
即我们使用：
$$C_{2n}^n-C_{2n}^{n-1}=\frac{C_{2n}^n}{n+1}=\frac{A_{2n}^n}{A_n^n\ast (n+1)}$$

但是我们由于要取模，所以我们要对分母用逆元算。

3、代码

#include
using namespace std;
typedef long long LL;
const int N=1e5+10;
const int mod=1e9+7;
LL qmi(LL a,LL b,LL p)
{
    LL res=1;
    while(b)
    {
        if(b&1)
        res=a*res%p;
        a=a*a%p;
        b>>=1;
    }
    return res;
}
int main()
{
    int n;
    cin>>n;
    LL res=1;
    int a=2*n,b=n;
    for(int i=a;i>(a-b);i--)res=res*i%mod;
    for(int i=1;i<=b;i++)res=res*qmi(i,mod-2,mod)%mod;
    res=res*qmi(n+1,mod-2,mod)%mod;
    cout<<res<<endl;
    return 0;
}