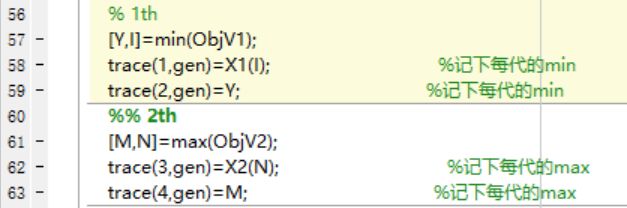遗传算法求函数的最值问题

一、遗传算法概述

遗传算法（Genetic Algorithm，GA）最早是由美国的 John holland于20世纪70年代提出,该算法是根据大自然中生物体进化规律而设计提出的。是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法。该算法通过数学的方式,利用计算机仿真运算,将问题的求解过程转换成类似生物进化中的染色体基因的交叉、变异等过程。在求解较为复杂的组合优化问题时,相对一些常规的优化算法,通常能够较快地获得较好的优化结果。遗传算法已被人们广泛地应用于组合优化、机器学习、信号处理、自适应控制和人工生命等领域。

二、算法过程

（1）初始化：设置进化代数计数器t=0，设置最大进化代数T，随机生成M个个体作为初始群体P(0)。

（2）个体评价：计算群体P(t)中各个个体的适应度。

（3）选择运算：将选择算子作用于群体。选择的目的是把优化的个体直接遗传到下一代或通过配对交叉产生新的个体再遗传到下一代。选择操作是建立在群体中个体的适应度评估基础上的。

（4）交叉运算：将交叉算子作用于群体。遗传算法中起核心作用的就是交叉算子。

（5）变异运算：将变异算子作用于群体。即是对群体中的个体串的某些基因座上的基因值作变动。群体P(t)经过选择、交叉、变异运算之后得到下一代群体P(t+1)。

（6）终止条件判断：若t=T,则以进化过程中所得到的具有最大适应度个体作为最优解输出，终止计算。

遗传操作包括以下三个基本遗传算子(genetic operator):选择(selection)；交叉(crossover)；变异(mutation)。

1、选择

从群体中选择优胜的个体，淘汰劣质个体的操作叫选择。选择算子有时又称为再生算子(reproduction operator)。选择的目的是把优化的个体(或解)直接遗传到下一代或通过配对交叉产生新的个体再遗传到下一代。选择操作是建立在群体中个体的适应度评估基础上的，常用的选择算子有以下几种：适应度比例方法、随机遍历抽样法、局部选择法。

2、交叉

在自然界生物进化过程中起核心作用的是生物遗传基因的重组(加上变异)。同样，遗传算法中起核心作用的是遗传操作的交叉算子。所谓交叉是指把两个父代个体的部分结构加以替换重组而生成新个体的操作。通过交叉，遗传算法的搜索能力得以飞跃提高。

3、变异

变异算子的基本内容是对群体中的个体串的某些基因座上的基因值作变动。依据个体编码表示方法的不同，可以有以下的算法：

a)实值变异。

b)二进制变异。

一般来说，变异算子操作的基本步骤如下：

a)对群中所有个体以事先设定的变异概率判断是否进行变异

b)对进行变异的个体随机选择变异位进行变异。

遗传算法引入变异的目的有两个:一是使遗传算法具有局部的随机搜索能力。当遗传算法通过交叉算子已接近最优解邻域时，利用变异算子的这种局部随机搜索能力可以加速向最优解收敛。显然，此种情况下的变异概率应取较小值，否则接近最优解的积木块会因变异而遭到破坏。二是使遗传算法可维持群体多样性，以防止出现未成熟收敛现象。此时收敛概率应取较大值。

4、终止条件

当最优个体的适应度达到给定的阈值，或者最优个体的适应度和群体适应度不再上升时，或者迭代次数达到预设的代数时，算法终止。预设的代数一般设置为100-500代。

三、源码及其分析

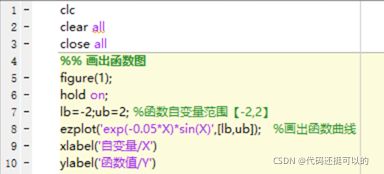
1、在Matlab上绘制所求函数的图像，如图3-1所示。

图3-1 绘制函数图像

所求的函数为 y=ⅇ-0.05xsinx，取值范围是-2到2之间。

2、初始化并配置相关参数，如图3-2所示。

图3-2 相关参数配置

NIND是个体数目，表示的初始随机选择的几个数字；MAXGEN表示的是最大的遗传代数，即循环的次数；PRECI表示的是变量的二级制位数；GGAP表示的是代沟；px表示的是交叉概率；pm表示的是变异概率。

需要把初值gen即循坏的开始定义为0，方便后面进行循环，同时要初始化种群，这里只需要调用遗传算法中自带的函数crtbp即可。需要特别注意的是我在这里面把FieldD、Chrom、X、ObjV进行了复制，即用两个相同的参数，这是为了方便后续进行遗传循环的时候分别求最大值最小值做铺垫。

3、遗传循环，具体代码如图3-3所示。

图3-3 遗传循环

这里面的循环主要分为两部分，第一部分是求最小值，第二部分是求最大值。第一部分求最小值代码如图3-4所示。

图3-4 求最小值

同样在循环迭代中，每次循环都需要对一些参数进行重新配置：适应度值、选择、重组、变异、自带个体的十进制转换、计算子代的目标函数、生成新种群。其中选择、重组、变异都是至关重要的三步骤，也是遗传算法中的关键。

求最大值也是同样的道理，具体代码如图3-5所示。

图3-5 求最大值

最小值很最大值的算法中，唯一不同的是在求最大值的时候他会把函数值进行一个求负的操作，同时还多了一个max的函数，在求最小值的时候是min函数。

4、把最小值的点和最大值的点存在数组里，具体代码如图3-6所示。

图3-6 记录最大值和最小值

5、在图像上画出最值的点，并且输出最值的结果，如图3-7，3-8所示。

图3-7 输出最大值和最小值

图3-8 运行结果

 

四、结果分析

其实在遗传算法中，他就是类似与进化论一样，优胜劣汰，根据你给定的条件，他就会朝着给定的方向走。因为我们给定的是最大值和最小值的条件，那么他就会往最大值和最小值的方向走，但是每一次都是随机的，所以就会取每一代中最大的和最小的再进行下一轮的迭代，因为我们给定的是20次迭代，如果说给的迭代次数越多，那么他的效果就会更加接近真值，就会离正真的最值更近。但是在这个问题中，我们也不用求得那么准确，大概接近就可以达到我们的要求。

五、附录代码

clc
clear all
close all
%% 画出函数图
figure(1);
hold on;
lb=-2;ub=2; %函数自变量范围【-2,2】
ezplot('exp(-0.05*X)*sin(X)',[lb,ub]);   %画出函数曲线
xlabel('自变量/X')
ylabel('函数值/Y')

%% 定义遗传算法参数
NIND=40;        %个体数目
MAXGEN=20;      %最大遗传代数
PRECI=20;       %变量的二进制位数
GGAP=0.95;      %代沟
px=0.7;         %交叉概率
pm=0.01;        %变异概率
trace=zeros(2,MAXGEN);                        %寻优结果的初始值
FieldD1=[PRECI;lb;ub;1;0;1;1];                      %区域描述器
Chrom1=crtbp(NIND,PRECI);                      %初始种群
%% 优化
gen=0;                                  %代计数器
X1=bs2rv(Chrom1,FieldD1);                 %计算初始种群的十进制转换
ObjV1=exp(-0.05*X1).*sin(X1);        %计算目标函数值

%% 2th
FieldD2=FieldD1;
Chrom2=Chrom1;
X2=X1;
ObjV2=ObjV1;

while gen