【算法设计与分析基础(第三版)习题答案】8.2 背包问题和记忆功能
【算法设计与分析基础 - 第三版 习题答案】8.2 背包问题和记忆功能
- 题 1
-
- 1. a
- 1. b
- 1. c
- 题 2
-
- 2. a
- 2. b
- 题 3
-
- 3.a
- 3.b
- 3.c
- 题 4
-
- 4.a
- 4.b
- 解析:
- 题 5
- 题 6
- 题7
- 题 8
- 题9
-
- 9.a
- 9.b
- 9.c
题 1
a. 对于下列背包问题的实例,应用自底向上动态规划算法求解。
b. a 中的实例有多少不同的最优子集
c. 一般来说,如何从动态规划算法所生成的表中判断出背包问题的实例是不是具有不止一个最优子集?
承重量
W = 6
| 物品 | 重量 | 价值 |
|---|---|---|
| 1 | 3 | 25 |
| 2 | 2 | 20 |
| 3 | 1 | 15 |
| 4 | 4 | 40 |
| 5 | 5 | 50 |
1. a
题目中要求使用自底向上的动态规划算法求解,所以我们可以使用动态规划的思想,具体代码如下:
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Author : David
from typing import List
def show_dp(dp: List[List[int]]) -> None:
for item in dp:
for num in item:
print(num, end="\t")
print()
def knapsack_problem(weight: List[int], value: List[int], wp: int) -> int:
"""
背包问题,动态规划解决思路
在所有的物品之前添加一个重量为零, 价值为零的物品, 保证物品的下标从1开始
但是此时应该返回 dp[n-1][wp]
:param weight: 物品重量
:param value: 物品价值
:param wp: 背包承重
:return: 背包能够装的最大价值
"""
weight = [0] + weight
value = [0] + value
n = len(weight)
# 定义 dp[i][j] 表示 能够放进承重量为j的背包中的前i个物品中最有价值子集的总价值
# dp 的行数为 n + 1, 列数为 wp + 1
# 根据定义可知 dp[0][j] = 0, dp[i][0] = 0, 即第一行和第一列都为 0
dp = [[0] * (wp + 1) for _ in range(n)]
for j in range(wp + 1):
for i in range(n):
if i == 0 or j == 0:
dp[i][j] = 0
else:
if j < weight[i]:
dp[i][j] = dp[i - 1][j]
else:
dp[i][j] = max(dp[i - 1][j], value[i] + dp[i - 1][j - weight[i]])
show_dp(dp) # 输出 dp 数组
return dp[n - 1][wp]
if __name__ == '__main__':
weight = [3, 2, 1, 4, 5] # 物品重量
value = [25, 20, 15, 40, 50] # 物品价值
weight_backpack = 6 # 背包的承重
print(knapsack_problem(weight, value, weight_backpack))
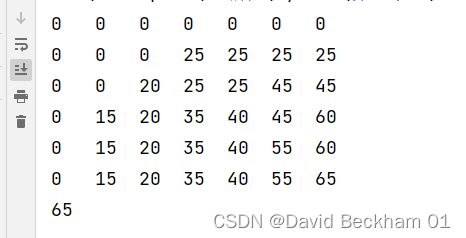
运行结果如下图所示:
1. b
我觉得题目应该想问有多少种选择的方案可以使得背包中的物品总价值最大。换句话说,有多少种选择的方案使得物品的重量不超过6且物品总价值为65 具体方案如下
方案一:通过
1.a中的运行结果我们不难看出,只有选择物品3 + 物品5的时候,背包中物品的总价值最大 ,最大总价值为65
1. c
- 我们可以直接观察二维数组
dp的最后一列,如果最后一列中存在多个最大值,则可以判定背包问题的实例中存在不止一个最优子集。- 因为从定义中我们可以知道二维数组
dp的最后一列表示的是,从所有物品中选择,放入称重量为 j (0<=j<=W), 能获得的最大价值,所以如果二维数组dp的最后一列中存在多个最大值则表示背包问题存在不止一个最优子集
题 2
a. 为背包问题写一段自底向上的动态规划算法的伪代码。
b. 写一段伪代码,使得可以从背包问题的自底向上动态规划算法生成的表中求得最优子集的组成。
2. a
F[0][] ← {0} # 第 0 行全部赋值为 0
F[][0] ← {0} # 第 0 列全部赋值为 0
for i←1 to N
do for k←1 to V
F[i][k] ← F[i-1][k] # 首先默认背包不装第 i 件物品
if(k >= C[i])
# 如果背包要装第 i 件物品,则需要找出装与不装的最大收益
then F[i][k] ← max(F[i][k],F[i-1][k-C[i]]+W[i])
return F[N][V]
2. b
# dp 为已经填好的二维数组,
# weight 物品重量的数组
# value 物品价值的数组
# wp 背包的承重量
row ← len(weight)
col ← wp
remain ← dp[-1][-1]
path ← list()
while remain != 0
do if dp[row][col] != dp[row - 1][col]
do remain -= value[row - 1]
col -= weight[row - 1]
path.append(row)
row += 1
row -= 1
return path
题 3
对于背包问题的自底向上动态规划算法,请证明:
a. 它的时间效率属于O(nW) 。
b. 它的空间效率属于O(nW)。
c. 从一张填好的动态规划表中求得最优子集的组合所用的时间属于O(n)。
3.a
首先,我们从背包问题中可以看出,我们需要按行 填写 二维数组
dp,所以需要计算的次数为row * col其中row为dp的行数,col为dp的列数,我们一般使用最坏的情况来计算时间复杂度,所以我们可以知道背包问题的时间复杂度为O(row * col)。
3.b
其次,使用记忆功能法,也需要 填写 二维数组
dp, 虽然记忆功能法的计算次数会少一些,但是递归会造成更多的内存空间的使用。我们一般使用最坏的情况来计算时间复杂度,所以我们可以知道记忆化功能法的时间复杂度也为O(row * col)。
3.c
从下面的代码里面我们可以看出,
求最优子集的组合的算法时间复杂度在最坏的情况下为O(n), 这种情况下,我们选取了所有的物品
def get_path(dp: List[List[int]], weight: List[int], value: List[int], wp: int) -> None:
weight, value = weight[1:], value[1:]
row, col, remain = len(weight) - 1, wp, dp[-1][-1]
path = list()
while remain != 0:
if dp[row][col] != dp[row - 1][col]:
remain -= value[row - 1]
col -= weight[row - 1]
path.append(row)
row += 1
row -= 1
print(path)
题 4
a. 判断正误: 背包问题实例的动态规划表中某一行的序列总是非递减的。
b. 判断正误: 背包问题实例的动态规划表中某一列的序列总是非递减的。
4.a
正确
4.b
正确
解析:
我们先看一个例子:
weight = [3, 2, 1, 4, 5] # 物品重量
value = [25, 20, 15, 40, 50] # 物品价值
weight_backpack = 6 # 背包的承重
根据定义,dp[i][j] 表示从前 i 件物品中选择,放入承重量为 j 的背包中,能获得的最大价值 我们不难发现一定会存在 :
dp[i][j] >= dp[i][j-1]dp[i][j] >= dp[i-1][j]
所以 题4 中的4.a和4.b都是正确的
题 5
假设n种物品中每种物品的数量不限,为该背包问题设计一个动态规划算法并分析该算法的时间效率。
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Author : David
from typing import List
def show_dp(dp: List[List[int]]) -> None:
for item in dp:
for num in item:
print(num, end="\t")
print()
def func_1(weight: List[int], value: List[int], wp: int) -> int:
n = len(weight) # 物品数量
weight, value = [0] + weight, [0] + value
dp = [[0 for _ in range(wp + 1)] for _ in range(n + 1)]
for i in range(1, n + 1):
for j in range(1, wp + 1):
if weight[i] > j:
dp[i][j] = dp[i - 1][j]
else:
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i - 1]] + value[i - 1])
show_dp(dp)
get_path(dp, weight, value, wp)
return dp[-1][-1]
class Solution(object):
def fullbag(self, weight: List[int], value: List[int], wp: int) -> int:
return func_1(weight, value, wp)
def Main(self):
weight = [3, 2, 1, 4, 5] # 物品重量
value = [25, 20, 15, 40, 50] # 物品价值
weight_backpack = 6 # 背包的承重
print(self.fullbag(weight, value, weight_backpack))
if __name__ == '__main__':
Solution().Main()
复杂度分析:
- 时间复杂度:
O(nw),计算的次数为row * col其中row为dp的行数,col为dp的列数 - 空间复杂度:
O(nw),同上
题 6
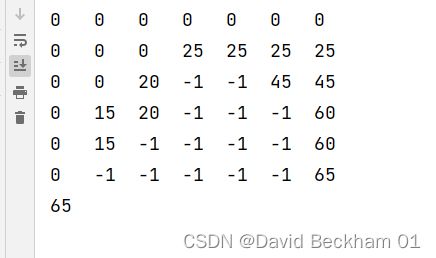
对第1题中给出的背包问题的实例应用记忆功能方法。在动态规划表中找出这样的单元格:
- 在这个实例中,从来没有被记忆功能方法计算过的单元格;
- 不需要重新计算就能使用的单元格。
- 没有呗记忆功能法计算过的单元个有:
(3,4),(3,5),(4,4),(4,5),(4,6),(5,3),(5,4),(5,5),(5,6),(6,2),(6,3),(6,4),(6,5),(6,6),共 14 个单元格 - 除去
1中提到的 14 个单元格, 其他单元格都不需要重新计算即可使用
题7
证明背包问题的记忆功能算法的时间效率类型和自底向上算法是相同的(参见第3题)。
- 首先,我们从背包问题中可以看出,我们需要按行 填写 二维数组
dp,所以需要计算的次数为row * col其中row为dp的行数,col为dp的列数,我们一般使用最坏的情况来计算时间复杂度,所以我们可以知道背包问题的时间复杂度为O(row * col)。 - 其次,使用记忆功能法,也需要 填写 二维数组
dp, 虽然记忆功能法的计算次数会少一些,但是递归会造成更多的内存空间的使用。我们一般使用最坏的情况来计算时间复杂度,所以我们可以知道记忆化功能法的时间复杂度也为O(row * col)。
题 8
为什么根据公式C(n, k) = C(n- 1,k- 1)+C(n - 1,k)计算二项式系数时,记忆功能法不是一个好方法?
- 首先,并不是不能实现使用记忆功能法计算二项式系数,使用记忆功能法会消耗一些内存空间,使得算法的空间复杂度为
O(nk) - 其次,我们可以使用递归的方式求二项式的系数,这样不需要开辟一个二维数组来存储已经计算出来的值,可以节约一部分空间,使算法的空间复杂度达到
O(1) - 最后,下面我给出两种不同的算法的代码
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Author : David
def func_1(n: int, k: int) -> int:
"""
方法一:使用自顶向下的方式计算二项式系数
:param n:
:param k:
:return:
"""
dp = [[-1] * (k + 1) for _ in range(n + 1)]
# 初始化数据第 0 列为 0
for i in range(len(dp)):
dp[i][0] = 1
# 初始化数据第 0 行为 0
for j in range(len(dp[0])):
dp[0][j] = 1
dp[j][j] = 1
def func(x: int, y: int) -> int:
if dp[x][y] < 0:
dp[x][y] = func(x - 1, y - 1) + func(x - 1, y)
return dp[x][y]
return func(n, k)
def func_2(n: int, k: int) -> int:
"""
方法二:使用递归的方式计算二项式系数
:param n:
:param k:
:return:
"""
if k == 0:
return 1
if n == 0:
return 0
return func_2(n - 1, k) + func_2(n - 1, k - 1)
if __name__ == '__main__':
n, k = 8, 3
print(func_1(n, k))
print(func_2(n, k))
题9
针对下面某一种著名的动态规划方法的应用写一个研究报告。
a。求两个序列中最长的公共子序列。
b。最优串编辑。
c.多边形的最小三角剖分。
9.a
原文链接: python实现最长公共子序列(LCS)
- 找到公共子序列的长度
若a为空或b为空,最长公共子序列为0
若a[m-1] == b[n-1](a的最后一个元素 == b的最后一个元素),那么a[:m]和b[:n]的公共子序列就是a[:m-1]和b[:n-1]
的公共子序列 + 1
若a[m-1] != b[n-1],那么a[:m]和b[:n]的公共子序列就是 MAX(a[:m-1]和b[:n]的公共子序列, a[:m]和b[:n-1]的公共子序列)- 找到具体的公共子序列
返方向推,从dp表中元素(a[m-1], b[n-1])(右下方最后一个元素)开始判断,如果相等的话,取a出来并放到res=""中,
然后回退到(a[m-2], b[m-2]),如果不等的话,取 MAX(a[m-2], b[m-1], (a[m-1], b[m-2]))
"""
计算最长公共子序列的长度
"""
def lcs(str1, str2, dp):
len1 = len(str1)
len2 = len(str2)
for i in range(1, len1+1): # dp表第一行和第一列元素为0,所以i和j要从1开始,到最后一个元素len1+1
for j in range(1, len2+1):
if str1[i-1] == str2[j-1]: # i=1时字符串从a[0]开始
dp[i][j] = dp[i-1][j-1] + 1
else:
dp[i][j] = max(dp[i-1][j], dp[i][j-1])
return dp[len1][len2] # dp表右下角最后一个元素为最长公共子序列长度
"""
计算具体的公共子序列
"""
def getlcs(str1, str2, dp):
i = len(str1)
j = len(str2)
res = " "
while(i != 0 and j != 0): # 两个字符串最后一个元素相等的话,选择一个字符串中的元素添加到res=" "中
if(str1[i-1] == str2[j-1]):
res += str1[i-1]
i -= 1
j -= 1
else:
if(dp[i][j] == dp[i-1][j]): # dp[i][j]从左边来还是从上边来
i -= 1
else:
j -= 1
return res[::-1] # res是从右往左的字符串,所以要逆序将其输出为从左往右的字符串
str1 = "bdcaba"
str2 = "abcbda"
lenA = len(str1)
lenB = len(str2)
dp = [[0 for i in range(lenA+1)] for j in range(lenB+1)] # 生成一个行为lenB+1,宽为lenA+1的二维数组
length = lcs(str1, str2, dp)
print("最长公共子序列长度为:", length)
print("dp表为:", dp)
res = getlcs(str1, str2, dp)
print("最长公共子序列为:", res)
9.b
原文链接: 最优编辑 - 雪浪snowWave - 博客园
题目:对于两个字符串A和B,我们需要进行插入、删除和修改操作将A串变为B串,定义c0,c1,c2分别为三种操作的代价,请设计一个高效算法,求出将A串变为B串所需要的最少代价。给定两个字符串A和B,及它们的长度和三种操作代价,请返回将A串变为B串所需要的最小代价。保证两串长度均小于等于300,且三种代价值均小于等于100。
思路:生成dp[n+1][m+1]的二维表,列代表s1,开头第一个是空,行代表s2,开头第一个是空,dp[i][j]代表s1[0,i]生成s2[0,j]的最小代价,比如s1=“ab12cd3”,s2=“abcdf”,那么dp[0][0]=0,dp[1][0]就是把s1的第一位‘a’变成空,即删除’a’,依次类推求得第一列,同理第一行就是每次增加字符到s1[1,i],故也可求得第一行。dp[i][j]分为四种情况,1.s1增加一个字符到s2 ic+dp[i-1][j] 2.s1删除一个字符到s2 dp[i][j-1]+dc 3.s1和s2之前相同,当前不相同,替换当前 dp[i-1][j-1]+rc 4 .s1和s2之前相同,当前也相同,那么dp[i][j]就和dp[i-1][j-1]相同.
public int findMinCost(String A, int n, String B, int m, int c0, int c1, int c2) {
int[][] dp = new int[n+1][m+1];
dp[0][0] = 0;
for(int i=1;i<=n;i++){
dp[i][0]=i*c1;
}
for(int i=1;i<=m;i++){
dp[0][i]=i*c0;
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(A.charAt(i-1)!=B.charAt(j-1)){
dp[i][j]=Math.min(dp[i-1][j-1]+c2,Math.min(dp[i-1][j]+c1,dp[i][j-1]+c0));
}else
dp[i][j]=dp[i-1][j-1];
}
}
return dp[n][m];
}
9.c
原文链接:多边形三角剖分的最小值 python
v[i][j]
从顶点i到j组成的凸多边形
边界
v[i][i] = 0;
v[i][i + 1] = 0
v[i][i + 2] = A[i] * A[i + 1] * A[i + 2]
当多边形是三条边以上时(i + 2 < j)
v[i, j]可以通过一个三角形(i, j, k)划分为两部分
凸多边形v[i, k]
凸多边形v[k, j]
i.e:
v[i, j] = MIN(v[i][k] + v[k][j] + A[i] * A[k] * A[j]) (i < k < j)
from typing import List
from functools import lru_cache
class Solution:
def minScoreTriangulation(self, A: List[int]) -> int:
@lru_cache(None)
def v(i, j):
# recursive end
if i + 1 == j:
return 0
res = float('inf')
# search k that results in minum value
for k in range(i + 1, j):
res = min(res, v(i, k) + v(k, j) + A[i] * A[j] * A[k])
return res
return v(0, len(A) - 1)
if __name__ == "__main__":
a = Solution()
print(a.minScoreTriangulation([35,73,90,27,71,80,21,33,33,13,48,12,68,70,80,36,66,3,70,58]))