Determining watersheds in digital pictures via flooding simulations 论文翻译

论文翻译

该篇是论文《Determining watersheds in digital pictures via flooding simulations》的翻译版本，里面可能有很多翻译不到位的地方，希望各位谅解，最好是对照原文进行看，以更好的正确理解文章的真意。

摘要

分水岭变换是数学形态学提供的一种非常强大的图像分析工具。然而，现有的分水岭算法要么过于耗时，要么不够精确。本文的目的是介绍一种新的、可行的转换实现方法。它基于图像的渐进泛洪，适用于n维图像。像素首先按其灰度值的递增顺序排序。然后，对连续的灰度级进行处理，以模拟flooding的传播。分布排序技术与每个灰度级的宽度优先扫描相结合，使得计算速 度非常快。此外，由于该算法可以处理任何类型的数字网格，并且其对一般图的扩展也很简单，因此该算法非常通用。它对图像分割的兴趣体现在从有噪声的图像中提取几何形状、分离三维重叠粒子以及在图像和图形上使用分水岭分割数字高程模型(a digital elevation mode)。

1 介绍

在图像分析领域，尤其是数学形态学(MM)[20,21]中，通常将灰度图看作是地形图面，像素的灰度级代表其高地。这种表示方法用于更好地理解给定变换对所研究图像的影响。现在，让一滴水落在这样的地形表面。根据万有引力定律，它会沿着最陡的斜坡向下流动，直到达到最小值。地表最陡坡径达到给定最小值的所有点构成与此最小值相关的集水区盆地。分水岭是划分相邻流域盆地的区域。
正如人们所预料的那样，第一个分水岭算法是从数字高程模型(DEMs)[9]中提取地形划分。不幸的是，这个算法通常会导致较差的结果，正如[ 8,23]所解释的那样。同时，在独立于数字地形研究的基础上，对图像处理领域的分水岭变换进行了研究。该方法首次由Ch. Lantuejoul{14]提出，他后来与S. Beucher共同改进[2,3,4]。分水岭变换是MM提供的最强大的轮廓检测和图像分割工具之一[6,27,7]。许多算法已经被提出从数字图像中提取分水岭。事实证明，它们要么速度过慢(尤其是在传统计算机上)，要么甚至更糟——不准确[28]。在这里，我们介绍了一个新的和多用途的分水岭变换，适用于各种离散空间。在§2中，结果表明，基于洪水模拟的分水岭划分比基于最陡坡道的分水岭划分更适合于流域的形式化，在§ 3中，介绍了我们的实现，并详细介绍了它的两个主要步骤，排序和洪泛（注水）过程。然后，在§4中讨论了该算法的性能和优点。最后，§ 5用于一些应用程序，说明我们的算法在图像分割中的效率。

2 根据洪泛模拟定义watersheds

对数字函数分水岭概念的仔细研究表明，很难给出一个明确的定义。例如，当多个最陡的斜坡路径出现时，高原(台地)上的流向如何?此外，在处理离散函数时，最陡斜率路径的概念不适用于流域的实际实现，因为在数字函数[17]上不存在决定水滴遵循哪条路径的规则。在本节中，我们展示了通过洪水模拟来定义流域克服了这些困难。它可以被看作是一个算法定义，因为它允许开发一个精确的、通用的算法来计算分水岭变换(参见§3)。所有这些定义都是为n维图像制定的，但为了更方便起见，figures和一些解释是在2维的情况下给出的。
我们考虑一个N维灰度图I，其定义域记为DI，I取区间[0, N]内的离散值,N为任意正整数:

设G表示底层数字网格，它只是Zn x Zn的子集,我们记 NG§表示一个像素p关于G的邻域集合：

定义1 DI中两个像素点p和q之间长度为l的路径P是

给定路径P的长度记为l§。
定义 2 ：I高度h处的最小M是一个像素与h值相连的高原，其外边界像素值严格大于h。
根据这些初步的定义，我们现在将以洪水模拟的方式呈现分水岭[4,3]。假设函数的极小值按其灰度值的递增顺序排序，并在最低海拔处开始逐步淹没最小值的盆地。当水位达到第二个最小水位时，我们同时淹没两个流域，直到达到第三个最小水位，以此类推。此外，在来自两个不同盆地的水将合并的地方建立水坝(见图1)。在这一过程的末尾，每个最小值都被水坝完全包围，水坝将其相关联的流域划分开来。由此得到的大坝群对应于分水岭，并提供了I在不同流域的镶嵌。

图1:在两个不同的极小值处建造水坝
为了更形式化地表示这种泛洪模拟，表示灰度图像I在其域DI上取的最小值hmin，最大值hmax。其中，Th(I)为I 在h级的阈值：

我们也表示C(M)流域与最小M和Ch(M)流域相关的子集，该流域由海拔较低或等于h的点组成:

最后，Min (I)是指高度h处属于极小值点的集合。
现在我们需要回顾测地线距离[15,16]和测地线影响带的定义。假设A是一个单连通的集合。
定义3 A中x和y两个pixel之间的测地线距离dA(x，y)是A中连接x与y且包含在A中的路径长度的极小值:

定义4 A中的B的连通分量Bi的测地线影响区izA(Bi)是A的点的集合，其与Bi的测地线距离小于其与B的任何其他分量的测地线距离:

这个概念如图2所示。A中不属于任何测地线影响区域的点，通过A内B的影响区(SKIZ)构成骨架，记为SKIZA(B):

这些定义很容易扩展到A不是单连通，甚至根本不连通的情况。

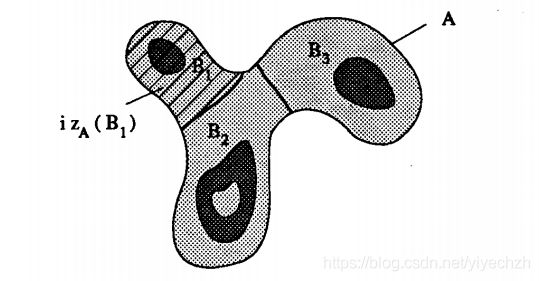
图2:连通分量B的测地线影响区，在集合A内。
为了模拟注水过程，我们从属于最低高度（lowest altitude）minima的点开始，即 这些点构成了递归的初始集合。我们因此设置:

现在考虑在级别hmin+1的I的阈值，即 ，Y是 的一个连通分量，之间可能存在三种包含关系:


这些包含关系如图3所示。既然所有的可能性都讨论过了，we take

作为递归的第二集合。这种关系当然适用于所有的h级，最后，我们得到如下结论:
定义5(集水盆地和分水岭通过洪泛模拟) 灰度图像I的集水盆地集合 等于 经过以下递归得到的集合Xh_max:

I的分水岭对应于Di中这个集合的补码，也就是以不属于任何集水区“盆地”的DI点集的集合。
图4给出了两个层次之间的递归关系。

3 算法

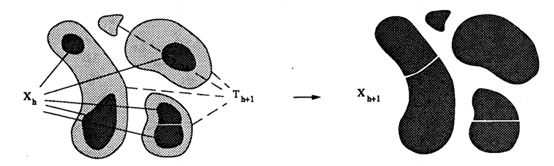
图4:Xn和Xn+1之间的递归关系。
分水岭算法的实现基于$ 2中的定义。因此，我们必须考虑被研究图像的连续阈值，并尽可能快地计算出一个阈值在另一个阈值内的测地线影响区。由于图像是逐灰度级处理的，每一步只能有效处理少量像素。因此，与其扫描整个图像来修改几个像素的值，还不如直接访问这些像素。这是通过对像素按其灰度值的递增顺序进行初步排序来实现的。在众多的排序技术中，分布排序[131]特别适合于目前的问题。该程序首先确定每个图像灰度级的频率分布。然后计算累积频率分布。这将导致将每个像素直接分配到排序数组中唯一的单元格。由于计算频率分布所需的内存和时间通常比图像所需的时间少得多，因此这种排序技术(与像素数成线性w.r.)是处理图像数据的最佳选择之一。
一旦像素被排序，通过对每个阈值水平的宽度优先扫描，就可以快速计算大地测量影响区域。这种扫描可以通过像素队列实现。假设洪泛已经完成，直到给定的h级-每个流域已经被找到。每个流域对应的最小高度小于或等于h的流域都应该有一个标签。由于之前的排序，可以直接访问高度h+1的像素。这些像素被赋予一个特殊的值，比如蒙版。其中已经标记像素为其邻居之一的像素将被放入队列中。队列结构通过计算测地线infuence zones(参见§2)，从这些像素点开始，通过计算geodesic infuence zones(参见§2)，可以扩展具有值掩模的像素点掩模内的标记集水池。事实上，它们并没有连接到任何已经被标记的集水区。因此，需要对h +1水平的像元进行第二次扫描，以检测仍然具有值掩模的像元，并为所发现的流域赋予一个新的标签。此外，还为两个不同流域合并的像素分配了一个特定的值wshed。正如KaTeX parse error: Expected 'EOF', got '#' at position 1003: …可获得准确的集水区和集水区。 #̲#4 评估 上面描述的分水岭过… 5.2)和其他离散空间，比如图。图上的分水岭构成了一个非常新颖的图像分割工具[26]，如§5.3所示。最后，本算法避免了大多数现有实现所陷入的经典陷阱(即高原问题和[28,29]中描述的厚“流域区域”配置)，使得的精度非常显著。

5 应用

5.1分水岭与图像分割

与MM提供的其他工具相结合，分水岭变换构成了一个强大的轮廓检测和图像分割过程(4,6,27,7)。本节以几何形状[10]噪声图像的分割为例说明了该方法(见图6)。由于其对比度低、噪声高，加之其形态梯度[6]的流域计算简单，导致了相当大过分割,就是,将搜索到的轮廓丢失在大量无关的轮廓中。对原始图像进行初始滤波并不能解决这个问题。例如，图6b为先用交替序列滤波器[22]处理的原始图像的形态梯度，图6c为其对应的流域。为了避免过度分割，至少有两种方法可以选择:删除分水岭的不相关弧(后处理)，或者修改梯度函数，使其分水岭与目标的轮廓一致(预处理)。前者一般采用区域增长算法[11,19]。$ 5.3介绍了一种应用于过度分割DEM的后处理技术。对于图6a的分割，我们更倾向于先对梯度图像进行修改。它需要一些外部知识，因为它需要一个初始标记步骤。区域标记是指包含在该区域内的一组连通像素。每个对象和背景都需要标记。当标记被提取后，在[18]中讨论的形态学过程允许
1. 将这组标记作为梯度函数的极小值，同时删除所有其他极小值，
2. 保存位于标志之间的主要分水岭线。
这种变换通常称为梯度同伦的修正。计算这个修正梯度的分水岭，然后提供了所需的分割:背景标记的集水区代表背景本身，而分水岭对应于所需对象的轮廓。
根据该方案，要获得图6a的良好分割，需要确定ackground的标记和每个几何形状的标记。一个即时的解决方案包括手动标记这些对象，但是标记的自动提取是首选的。在原始图像(图6a)中，几何对象比背景颜色更深。因此，对这个图进行扩展，然后加上一个阈值，就可以提取对象标记(图6d)。目前还需要一个背景标记。利用分水岭变换，得到最高的顶线(即确定分离对象标记的原始图像的(白色区域)，并作为ackground标记。最后，使用整个标记集修改梯度的同伦’，如上所述。现在，几何形状的轮廓与修改后的梯度图6f中的流域精确对应。由于本文介绍的算法，这里描述的整个分割过程在SUN 4上运行不到10秒!

5.2 3-d watersheds 的应用

如前所述，本算法适用于任意连通度的n维图像:为每个像素考虑合适的邻域集就足够了。它的计算效率允许扩展§5.1中描述的处理三维图像的方法。目前正在开发医学图像和遥感领域的应用。为了说明三维流域，我们建议将图7a综合图像中部分重叠的文章进行分离。它是一个64×64×64的二进制图像，显示为64×64的二维图像(从左到右，从上到下)。根据[6]中描述的方法，首先计算相对距离函数，即的函数，该函数与与背景距离相反的每个特征点相关联(见图7b)。然后用距离反函数的分水岭将重叠粒子分离(见图7c)。该二值分割方法已应用于实际案例中，如大米颗粒[1]或咖啡豆[6]的二维分割。

5.3 图上的分水岭:DEMs的应用

通过形态学变换研究的数字图像通常是按照正方形或六角形图进行数字化的，但是我们可以很好地想象使用一般图并应用相同的处理方法。实际上，所有不涉及任何方向概念的欧几里德形态学变换都可以很容易地转到这些欧几里德几何中去[251]。特别是，通过食物模拟定义的分水岭扩展到图。在实践中，使用顶点而不是像素就足够了，通过允许直接访问给定顶点[26]的邻居的数据结构来编码图形

图6:使用分水岭变换分割有噪声的几何形状

图7:三维重叠粒子的分离
图上的分水岭提供了图像[26]的分层分解，这是其他(形态学)分解的替代方法，比如基于开口和闭合[12]的分解。它们在形态学区域生长方法上也有很好的应用前景。基于这些思想的算法已经被S. Beucher成功地用于道路图像分割[5,7]。
为了在图中显示分水岭，对图8所示的DEM进行了处理。它表示一个256 x 256的海拔矩阵，具有50米的x-y分辨率。将分水岭变换应用于图8a，得到图8b。在这一点上观察到的令人失望的过度分割是由于模型中存在大量的极小值。这些极小值通常是由于工件或数据错误造成的。为了通过分水岭变换得到模型的良好划分，必须考虑预处理或后处理技术(见$5.1)。本文介绍了一种基于图上分水岭的DEM后处理技术，它不需要修改DEM的同伦(homotopy)性来去除其最小值[23]。为了从图8b中构建十进制图，每个流域(catchment basin)7/5/2019对应一个顶点。给定顶点的数值由与该顶点相关的分水岭线上的最小值决定。如果在共享分水岭线上存在先前计算的最小值，则两个顶点由一条边连接。通过计算该图上的分水岭变换，得到如图8c所示的分割结果。它现在与真实的地形特征相对应。

图8:利用图上的分水岭分割DEM。

6 总结

在图像处理领域，每个从业者都知道算法的计算效率是一个至关重要的问题。到目前为止，所有现有的分水岭实现要么花费了太多时间(即使是在专门的体系结构上)，要么不准确。现在算法也比简单地摆脱这些缺点,因为它也特别灵活:它适应各种各样的数字空间非常简单,其二维,三维图版本得到图像分割被简要地说明。除了这些例子的教学方面，我们的算法已经被用于复杂的分段任务，并有望对分水岭的使用提供新的见解。目前，它作为一种分割三维和彩色图像的工具正受到特别的研究。

python 代码实现

'''
input:decimal image
output:image of the labelled watersheds :the labels are 1,2,3,tec
flag:用于检测当前分配给像素p的值WSHD是否来自于p邻域内的另一个WSHD像素，而不是来自两个标签不同的相邻像素。
'''
import numpy as np
from collections import deque
import cv2 as cv
class Watershed(object):
   MASK = -2   #阈值水平的初始值（initial value of a threshold level）
   WSHD = 0    #分水岭
   INIT = -1   #label被初始化的值
   INQE = -3   #入队列标志

   def __init__(self, levels = 256):
      self.levels = levels

   # 找到相邻像素(记录的是坐标值)，包括给定像素p
   def _get_neighbors(self, height, width, pixel):
      return np.mgrid[
         max(0, pixel[0] - 1):min(height, pixel[0] + 2),
         max(0, pixel[1] - 1):min(width, pixel[1] + 2)
      ].reshape(2, -1).T

   def apply(self, image):
      current_label = 0
      flag = False
      fifo = deque()   #队列，先进先出

      height, width = image.shape
      total = height * width   #总共的像素点数量
      labels = np.full((height, width), self.INIT, np.int32)  #初始化为值为-1的array,shape为图像的高宽

      #将所有像素点压缩成了一行
      reshaped_image = image.reshape(total)

      # pixes是图像的每个像素点的‘坐标对’，比如（0,0），（0,1）
      pixels = np.mgrid[0:height, 0:width].reshape(2, -1).T   #height*width行2列,是一个array
      # 每个像素相邻像素的坐标。p代表一个坐标对 比如[0 0]
      neighbours = np.array([self._get_neighbors(height, width, p) for p in pixels])
      if len(neighbours.shape) == 3:
         # 所有像素具有相同数量的邻居
         neighbours = neighbours.reshape(height, width, -1, 2)
      else:
         # 像素可能具有不同数目的像素的情况
         neighbours = neighbours.reshape(height, width)

      indices = np.argsort(reshaped_image)    #将像素点进行升序排列，indices是排序后的索引值，不是真实的像素点值
      sorted_image = reshaped_image[indices]  #根据索引，进行像素点重新排列，sorted_image保存的是已经按像素点大小排列好的值
      sorted_pixels = pixels[indices]         #根据索引，将pixels坐标值也按照从小到大进行排列

      # levels的个数为256,也就是后面灰度值会被分为256个级别，为递增的等差数列，最小值为像素最低值，最大值为像素最高值
      levels = np.linspace(sorted_image[0], sorted_image[-1], self.levels)
      level_indices = []   #记录各个级别的像素下标
      current_level = 0

      # 获取排序以后图像每一个像素级别的第一个像素的索引值
      for i in range(total):   #total个像素，每一个像素都会被循环到
         if sorted_image[i] > levels[current_level]:
            # 跳过级别，直到达到下一个最高级别。
            while sorted_image[i] > levels[current_level]: current_level += 1   #最多有256各级别，也就是0~255
            level_indices.append(i)
      level_indices.append(total)   #得到是每一个像素级别的第一个像素的索引值，leve_indices是一个列表

      start_index = 0
      for stop_index in level_indices:    #对每个级别的像素进行操作，对应到sorted_image的像素值的下标
         # 屏蔽当前级别的所有像素。将该级别的labels值全部赋值为-2，该for循环的目的就是找出满足条件的点加入队列fifo
         for p in sorted_pixels[start_index:stop_index]:   #以行为单位进行操作，p是坐标对
            labels[p[0], p[1]] = self.MASK    #labels初始全为-1，将符合要求的地方重赋值为-2
            # 在当前级别使用现有盆地的邻居初始化队列。
            for q in neighbours[p[0], p[1]]: #只要p点的邻居中有一个label值大于等于0，p点就会进入队列，且p点会被标记为-3
               if labels[q[0], q[1]] >= self.WSHD:   # WSHD=0，label是初始化全为-1的array
                  labels[p[0], p[1]] = self.INQE     # INQE=-3，
                  fifo.append(p)                     #当前点进入队列
                  break

         # 扩展盆地，淹没过程.
         while fifo:  #该级别fifo队列里面还有值，则继续处理
            p = fifo.popleft()
            # 通过检查邻居来标记p
            for q in neighbours[p[0], p[1]]:
               #不要在外部循环中设置lab_p，因为它可能会更改。
               lab_p = labels[p[0], p[1]]
               lab_q = labels[q[0], q[1]]
               if lab_q > 0:  #邻居大于0
                  if lab_p == self.INQE or (lab_p == self.WSHD and flag):  #lab_p为-3，在队列的标志或者（为0且flag为真）
                     labels[p[0], p[1]] = lab_q  #lab_p会改变，值大于0
                  elif lab_p > 0 and lab_p != lab_q: #lab_p>0且跟当前lab_q不相等
                     labels[p[0], p[1]] = self.WSHD  #lab_p会被赋值为0
                     flag = False
               elif lab_q == self.WSHD:  #lab_q==0
                  if lab_p == self.INQE:
                     labels[p[0], p[1]] = self.WSHD
                     flag = True
               elif lab_q == self.MASK:  #lab_q==-2
                  labels[q[0], q[1]] = self.INQE  #将q送入队列
                  fifo.append(q)

         # 检测和处理当前级别的新极小值。检查是否发现新的minima
         for p in sorted_pixels[start_index:stop_index]:
            # p在一个新的最小值内，创建一个新标签。
            if labels[p[0], p[1]] == self.MASK:  #mask=-2
               current_label += 1
               fifo.append(p)
               labels[p[0], p[1]] = current_label
               while fifo:
                  q = fifo.popleft()
                  for r in neighbours[q[0], q[1]]:
                     if labels[r[0], r[1]] == self.MASK:
                        fifo.append(r)
                        labels[r[0], r[1]] = current_label

         start_index = stop_index
      #np.savetxt("./labels.txt", labels)
      return labels

if __name__ == "__main__":

   from PIL import Image
   import matplotlib.pyplot as plt
    #该算法只能输入灰度图像，若是传入的是RGB图像，可借助opencv转换为灰度图，再调用watershed

   w = Watershed()
   image = cv.imread('./person.jpg', cv.IMREAD_GRAYSCALE)
   # image = np.array(Image.open('./t.jpg'))
   # blurred = cv.pyrMeanShiftFiltering(image, 10, 100)  # 去除噪点
   # gray = cv.cvtColor(blurred, cv.COLOR_BGR2GRAY) #转换为灰度图
   cv.imshow("gray", image)
   cv.waitKey(0)
   labels = w.apply(image)  #image
   plt.imsave('ttt.png', labels)
#   plt.imshow(labels, cmap='Paired', interpolation='nearest')
#   plt.show()