CS224N笔记(四) Lecture 7:循环神经网络RNN的进阶——LSTM与GRU
本文将介绍两种比RNN更好地应对梯度消失问题的模型结构——LSTM和GRU,文章以CS224N的课件和材料为基础,重点分析他们的结构特点和梯度计算,在梯度消失的解决策略上进行了深入探究,并进一步分析它们的优缺点和应用场景。
目录
- 一、背景知识
- 二、LSTM的原理与结构
-
- 1.模型结构
- 2. 如何解决梯度消失
- 三、GRU的原理与结构
- 四、LSTM与GRU的选择
- 五、RNN的其他变种模型
-
- 1. 双向RNN
- 2. 多层RNN
- 六、参考文献
一、背景知识
循环神经网络RNN由于模型结构上的缺陷,很容易引起梯度爆炸和梯度消失,梯度爆炸可以用梯度截断方法在一定程度上缓解其影响,但是梯度消失几乎是致命缺陷,没有什么好办法可以解决它,这使得训练变得困难,模型很可能只受短时约束,长时约束的作用被大大削弱,学习不到相隔较远的两个词之间的联系。本文介绍的两种新的神经网络结构LSTM和RNN,可以很好地应对这个问题。
二、LSTM的原理与结构
1.模型结构
LSTM在模型结构上相对于RNN而言有两大变动:
- 新增了三个独特的门结构,用来控制信息地流动
- 增添了细胞状态cell state,同时也保留了原来的隐状态hiden state
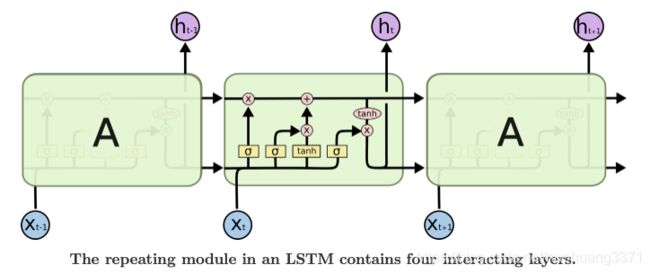
其整体的模型结构图如下所示,由多个结构相同的LSTM模块组成:
课件上这张图的来源于参考文献2,大家可以去看看那篇文章对LSTM每个步骤进行拆解,下面的公式讲以图中的符号为准,可能会与课件中有一点出入。
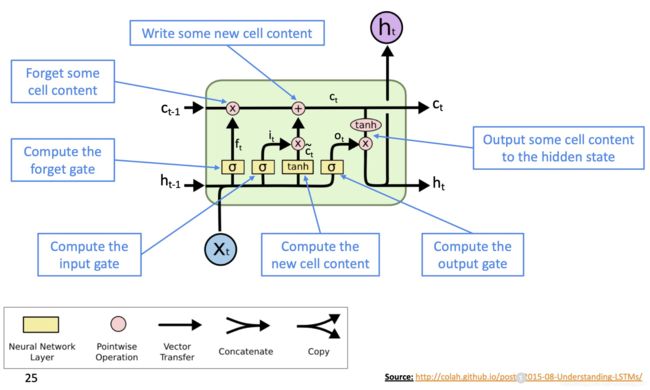
符号解释
细胞状态 C t C_t Ct: C t = f t ⊗ C t − 1 + i t ⊗ C ~ t C_t = f_t \otimes C_{t-1} + i_t \otimes \tilde{C}_{t} Ct=ft⊗Ct−1+it⊗C~t
细胞状态新内容 C ~ t \tilde{C}_t C~t: C ~ t = t a n h ( W c h t − 1 + U c x t + b c ) \tilde{C}_{t} = tanh(W_ch_{t-1}+U_cx_t+b_c) C~t=tanh(Wcht−1+Ucxt+bc)
隐状态 h t h_t ht: h t = o t ⊗ t a n h ( C t ) h_t=o_t \otimes tanh(C_t) ht=ot⊗tanh(Ct)
遗忘门 f t f_t ft: f t = σ ( W h h t − 1 + U f x t + b f ) f_t=\sigma(W_hh_{t-1}+U_fx_t+b_f) ft=σ(Whht−1+Ufxt+bf)
输入门 i t i_t it: f i = σ ( W i h t − 1 + U i x t + b i ) f_i=\sigma(W_ih_{t-1}+U_ix_t+b_i) fi=σ(Wiht−1+Uixt+bi)
输出门 o t o_t ot: f t = σ ( W h h t − 1 + U o x t + b o ) f_t=\sigma(W_hh_{t-1}+U_ox_t+b_o) ft=σ(Whht−1+Uoxt+bo)
三个门结构
LSTM的门结构充当信息的关口,它们决定了信息是否能够完全流通,取值范围都是(0, 1),0则完全不让通过,1则完全通过。三个门结构的计算方法是一模一样的,只是用了相互独立的参数,LSTM的参数量相比于RNN多了许多,一定程度上提高了模型容量。注意在参考文献2中的写法不太一样,但其实只是将两个参数 W W W和 U U U给合并了,本质上是一样的。
遗忘门会作用到上一时刻的细胞状态 C t − 1 C_{t-1} Ct−1,将句子中的一些历史内容遗忘掉,举个例子,一个句子中如果出现了he,那么模型可能会记住该信息,后面的谓语要用单数形式比如is,如果紧接着出现了they,那么模型可能需要忘掉之前的主语he,后面的谓语需要用复数形式are,当然这只是一个理想化的例子,真实模型具体编码了什么我们很难得知,这只是以人的思维赋予了模型它可能需要的能力。
输入门作用到细胞新内容 C ~ t \tilde{C}_t C~t,要添加到细胞状态的新内容也许不是全都需要,所以用输入门减小部分元素或者清零。这部分就相对抽象,因为细胞新内容 C ~ t \tilde{C}_t C~t和遗忘门一样也是通过 h t − 1 h_{t-1} ht−1和 x t x_t xt计算出来的,只是选用的激活函数不同,为什么要这么分两步走。可以这么想:细胞新内容 C ~ t \tilde{C}_t C~t是计算出了一些备选的新信息,输入门对这些信息进行挑选后再添加到细胞状态中。
输出门则是作用到细胞状态 C t C_t Ct中,从细胞状态中挑选出信息作为隐状态的输出。
细胞状态
LSTM中一个重要结构为细胞状态,值得详细展开,它贯穿整个LSTM模型,用来存储句子上下文信息,相当于RNN中将上下文信息编码在隐状态中,LSTM的细胞状态具有更强的信息保存能力,内容不容易被完全清除,也即能更好地捕捉长距离词语间的关系。为什么说它的内容不容易被完全清除,我们回顾它的计算方法:
C t = f t ⊗ C t − 1 + i t ⊗ C ~ t (1) C_t = f_t \otimes C_{t-1} + i_t \otimes \tilde{C}_{t} \tag{1} Ct=ft⊗Ct−1+it⊗C~t(1)
抛开遗忘门和输入门的作用不谈,当前时刻的细胞状态 C t C_t Ct,是上一时刻的细胞状态 C t − 1 C_{t-1} Ct−1与新添加的细胞内容 C ~ t \tilde C_t C~t的以相加的形式获得的,而RNN中上下文信息都放在 h t h_t ht中,它的计算过程中会通过参数矩阵 W h W_h Wh与上一隐状态 h t − 1 h_{t-1} ht−1以矩阵相乘的形式获得,并不断重复该过程,如果参数矩阵 W h W_h Wh的特征值都很小(或者模很小),那么在多次矩阵相乘过程中, h t h_t ht可能变得越来越小,上下文信息都已经丢失了。
那么有人可能会问,细胞状态一直这么加下去, C t C_t Ct不会到后面变得异常地大吗?确实是会这样,在初代的LSTM中,没有设置遗忘门,细胞状态的计算方式是:
C t = C t − 1 + i t ⊗ C ~ t C_t = C_{t-1} + i_t \otimes \tilde{C}_t Ct=Ct−1+it⊗C~t
这种形式的确非常容易使得细胞状态到后面异常地大,所以才设置了遗忘门 f t f_t ft,让它与上一时刻的细胞状态进行元素级相乘,有机会减小某些元素的值,甚至清零,这样就保证了细胞状态没有无节制地增长。
2. 如何解决梯度消失
LSTM的模型结构讲述完毕,但是仅从模型结构来看,还是很难解释为什么LSTM能够应对梯度消失。其实上面已经涉及到一点点,关键就是LSTM的细胞状态,它存储着句子的上下文信息,像一条传送带一样贯穿整个模型,而且是以相加元素级形式获得的。我们可以先感性地理解为什么不会梯度消失:
- LSTM中存在多条通路,多条通路的梯度以相加的形式汇聚,一条路的梯度为0不至于全部梯度为0
- LSTM中存在遗忘门和细胞状态,可以保证历史信息不那么容易被清除。
但是这么说还是还有抽象,我们来真正计算一下梯度。回顾前一篇文章中说RNN(链接文章)梯度消失主要是因为两个时刻间隐状态的梯度是 W h W_h Wh的幂次这种形式, W h W_h Wh如果很小,时间距离又很远的话,梯度就消失了:
∂ h ( t ) ∂ h ( i ) = ∏ j = i + 1 t ∂ h ( j ) ∂ h ( j − 1 ) = ∏ j = i + 1 t d i a g ( σ ′ ( W h h ( j − 1 ) + W e e ( t ) + b 1 ) ) × W h (2) \frac{\partial h^{(t)}}{\partial h^{(i)}} = \prod_{j=i+1}^t \frac{\partial h^{(j)}}{\partial h^{(j-1)}} = \prod_{j=i+1}^t diag(\sigma'(W_hh^{(j-1)}+W_ee^{(t)} + b_1)) \times W_h \tag{2} ∂h(i)∂h(t)=j=i+1∏t∂h(j−1)∂h(j)=j=i+1∏tdiag(σ′(Whh(j−1)+Wee(t)+b1))×Wh(2)
由于LSTM的上下文信息存储在细胞状态,我们重点来看下前后两个时刻细胞状态的梯度 ∂ C t ∂ C t − 1 \frac{\partial C_t}{\partial C_{t-1}} ∂Ct−1∂Ct。公式 ( 1 ) (1) (1)表明,C_t是关于 f t f_t ft, C t − 1 C_{t-1} Ct−1, i t i_t it, C ~ t \tilde{C}_{t} C~t的函数,而它们都是元素级乘法和加法,所以梯度相对好求,可以套用 ( u v ) ′ = u v ′ + u ′ v (uv)'=uv'+u'v (uv)′=uv′+u′v:
∂ C t ∂ C t − 1 = f t × ∂ C t − 1 ∂ C t − 1 + C t − 1 × ∂ f t ∂ C t − 1 + i t × ∂ C ~ t ∂ C t − 1 + C ~ t × ∂ i t ∂ C t − 1 = f t + C t − 1 × ∂ f t ∂ C t − 1 + i t × ∂ C ~ t ∂ C t − 1 + C ~ t × ∂ i t ∂ C t − 1 (3) \begin{aligned} \frac{\partial C_t}{\partial C_{t-1}} =& f_t \times \frac{\partial C_{t-1}}{\partial C_{t-1}} + C_{t-1} \times \frac{\partial f_t}{\partial C_{t-1}} + i_t \times \frac{\partial \tilde{C}_t }{\partial C_{t-1}} + \tilde{C}_t \times \frac{\partial i_t}{\partial C_{t-1}} \\ =& f_t + C_{t-1} \times \frac{\partial f_t}{\partial C_{t-1}} + i_t \times \frac{\partial \tilde{C}_t}{\partial C_{t-1}} + \tilde{C}_t \times \frac{\partial i_t}{\partial C_{t-1}} \end{aligned} \tag{3} ∂Ct−1∂Ct==ft×∂Ct−1∂Ct−1+Ct−1×∂Ct−1∂ft+it×∂Ct−1∂C~t+C~t×∂Ct−1∂itft+Ct−1×∂Ct−1∂ft+it×∂Ct−1∂C~t+C~t×∂Ct−1∂it(3)
上面关键就是第一项,由于 ∂ C t − 1 ∂ C t − 1 \frac{\partial C_{t-1}}{\partial C_{t-1}} ∂Ct−1∂Ct−1的结果是单位矩阵,所以第一项只剩下一个遗忘门 f t f_t ft,它不需要与其他矩阵相乘,所以只要遗忘门是1,可以保证 ∂ C t ∂ C t − 1 \frac{\partial C_t}{\partial C_{t-1}} ∂Ct−1∂Ct至少是一个1向量,这样损失函数 J t J_t Jt关于 C 1 C_1 C1的梯度 ∂ J t ∂ C t \frac{\partial J_t}{\partial C_t} ∂Ct∂Jt可以沿着细胞状态的通路无损地传送到下去,而不会在中途因为存在0向量所使得传到前面时梯度已经消失,即:
∂ J t ∂ C 1 = ∂ J t ∂ C t ∂ C t ∂ C t − 1 ∂ C t − 1 ∂ C t − 2 . . . ∂ C 2 ∂ C 1 ≠ 0 (4) \frac{\partial J_t}{\partial C_1} = \frac{\partial J_t}{\partial C_t} \frac{\partial C_t}{\partial C_{t-1}} \frac{\partial C_t-1}{\partial C_{t-2}} ...\frac{\partial C_2}{\partial C_{1}} \not= \bold{0} \tag{4} ∂C1∂Jt=∂Ct∂Jt∂Ct−1∂Ct∂Ct−2∂Ct−1...∂C1∂C2=0(4)
这里需要提醒大家注意,在知乎等平台上看到很多文章都喜欢引用或翻译文献4中的说法,那里也是计算了梯度 ∂ C t ∂ C t − 1 \frac{\partial C_t}{\partial C_{t-1}} ∂Ct−1∂Ct,通过 f t f_t ft这一项说明梯度不至于完全消失,本文也是借鉴了这种说法,但是那篇文章中, ∂ C t ∂ C t − 1 \frac{\partial C_t}{\partial C_{t-1}} ∂Ct−1∂Ct的计算是错误的:
图中等式两边红色方框的项都是 ∂ C t ∂ C t − 1 \frac{\partial C_t}{\partial C_{t-1}} ∂Ct−1∂Ct,两项完全一致,直接就消掉了,更离谱的是后边的 ∂ C t ∂ C t − 1 \frac{\partial C_t}{\partial C_{t-1}} ∂Ct−1∂Ct计算等于 f t f_t ft,这样等号左边的 ∂ C t ∂ C t − 1 \frac{\partial C_t}{\partial C_{t-1}} ∂Ct−1∂Ct还有什么好算的。只能说歪打正着,尽管 ∂ C t ∂ C t − 1 \frac{\partial C_t}{\partial C_{t-1}} ∂Ct−1∂Ct是会出现 f t f_t ft这独立的一项,但不是这样来的。

真正的计算方法应该是这样,从公式 ( 3 ) (3) (3)出发, i t i_t it, f t f_t ft, C ~ t \tilde{C}_{t} C~t都是关于 h t − 1 h_{t-1} ht−1的函数, h t − 1 h_{t-1} ht−1是又关于 C t − 1 C_{t-1} Ct−1的函数,这样我们根据链式法则,可以计算得到:
∂ C t ∂ C t − 1 = f t + C t − 1 × ∂ f t ∂ C t − 1 + i t × ∂ C ~ t ∂ C t − 1 + C ~ t × ∂ i t ∂ C t − 1 = f t + C t − 1 × ∂ f t ∂ h t − 1 ∂ h t − 1 ∂ C t − 1 + i t × ∂ C ~ t ∂ h t − 1 ∂ h t − 1 ∂ C t − 1 + C ~ t × ∂ i t ∂ h t − 1 ∂ h t − 1 ∂ C t − 1 (5) \begin{aligned} \frac{\partial C_t}{\partial C_{t-1}} =& f_t + C_{t-1} \times \frac{\partial f_t}{\partial C_{t-1}} + i_t \times \frac{\partial \tilde{C}_t}{\partial C_{t-1}} + \tilde{C}_{t} \times \frac{\partial i_t}{\partial C_{t-1}} \\ =&f_t + C_{t-1} \times \frac{\partial f_t}{\partial h_{t-1}}\frac{\partial h_{t-1}}{\partial C_{t-1}} + i_t \times \frac{\partial \tilde{C}_t}{\partial h_{t-1}}\frac{\partial h_{t-1}}{\partial C_{t-1}} + \tilde{C}_t \times \frac{\partial i_t}{\partial h_{t-1}}\frac{\partial h_{t-1}}{\partial C_{t-1}}\end{aligned} \tag{5} ∂Ct−1∂Ct==ft+Ct−1×∂Ct−1∂ft+it×∂Ct−1∂C~t+C~t×∂Ct−1∂itft+Ct−1×∂ht−1∂ft∂Ct−1∂ht−1+it×∂ht−1∂C~t∂Ct−1∂ht−1+C~t×∂ht−1∂it∂Ct−1∂ht−1(5)
这条公式最关键的还是第一项遗忘门 f t f_t ft,当它为1是梯度不至于消失,但是需要注意的是,它是否为1是由模型自己学习的,我们只能从结构上保证它有联系长距离上下文的能力,但也许长距离的上下文真的没有很强的关系呢?而在模型训练初始化时,一般还是会将遗忘门初始化为1,保证梯度能够无损地传递,从功能来理解,是认为所有上下文信息都需要保留,至于是不是真的要保留,交由模型在后续的训练中学习。
最后还有两点需要注意:
- 上面计算的是细胞状态通路的梯度,它不那么容易梯度消失,但是其他通路跟RNN很像,在梯度计算中仍然会出现参数矩阵的幂次,也是很有可能出现梯度消失的。LSTM解决梯度消失的最重要途径就是顶上细胞状态这一条传送带。
- LSTM并不保证完全不发生梯度消失,只是相比起RNN更加稳定。
三、GRU的原理与结构
LSTM中存在三个门结构,参数量较大,计算缓慢,因此有学者对它进行了以下精简:
- 将细胞状态和隐状态又重新合并成了单独的隐状态
- 将遗忘门和输入门合并成了更新门(update gate),它控制哪些信息需要进行更新,哪些信息进行保留
- 设置了重置门(reset gate),作用是控制旧的隐状态中的哪些内容可以参与新隐状态的计算
- 由于细胞状态和隐状态合二为一了,也就没有必要设置输出门了,输出门被删除
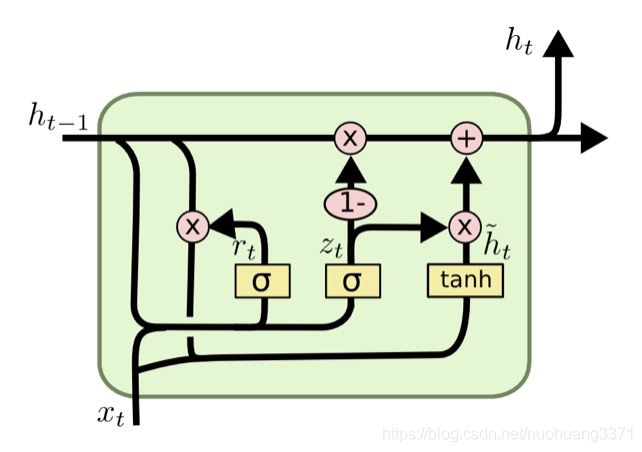
最终的模型结构如下,注意这幅图来自参考文献4,其中的符号和CS224N中所采用的不一致:
符号解释:
重置门 r t r_t rt: r t = σ ( W r h t − 1 + U r x t + b r ) r_t = \sigma(W_rh_{t-1} + U_rx_t +b_r) rt=σ(Wrht−1+Urxt+br)
更新门 z t z_t zt: z t = σ ( W z h t − 1 + U z x t + b z ) z_t = \sigma(W_zh_{t-1} + U_zx_t +b_z) zt=σ(Wzht−1+Uzxt+bz)
隐状态的新内容 h ~ t \tilde{h}_t h~t: h ~ t = t a n h ( W h ( r t ⊗ h t − 1 ) + U h x t + b h ) \tilde{h}_t = tanh(W_h(r_t \otimes h_{t-1})+U_hx_t+b_h) h~t=tanh(Wh(rt⊗ht−1)+Uhxt+bh)
隐状态 h t h_t ht: h t = ( 1 − z t ) ⊗ h t − 1 + z t ⊗ h ~ t h_t = (1-z_t) \otimes h_{t-1} +z_t \otimes \tilde{h}_t ht=(1−zt)⊗ht−1+zt⊗h~t
那么GRU能否应对梯度消失呢?答案是可以的,看到图中最上方那条贯穿的通路和LSTM中的细胞状态是不是很类似,而且同样也存在一个元素级加法操作,所以GRU中的隐状态与LSTM中的细胞状态一样,前后两个时刻间的梯度也会出现一个独立项,只不过是由遗忘门 f t f_t ft变成了更新门 z t z_t zt,只要更新门是1向量,至少可以保证 ∂ h t ∂ h t − 1 \frac{\partial h_t}{\partial h_{t-1}} ∂ht−1∂ht不会完全为0,隐状态通道上的梯度可以一直传递到最前方。
四、LSTM与GRU的选择
LSTM和GRU都能缓解了RNN中梯度消失的问题,使得长距离上下文信息的捕捉变得更加容易,但是LSTM参数量大,收敛较慢,计算耗时,GRU比起LSTM它的参数量较少,计算相对较快,也减少了过拟合的风险。但是具体该用哪一个,取决于数据量和效率要求,如果数据充足,LSTM可以提供更好的性能,如果要求计算快些,可以试试GRU。
五、RNN的其他变种模型
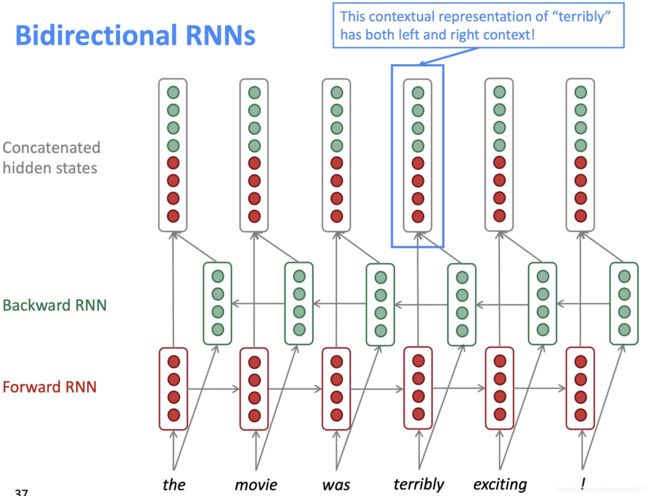
1. 双向RNN
我们前面说的上下文信息严格来说只是前文信息,后文是还没有输入到模型中的,但是有时候句子的关键信息可能是在后文出现,所以我们希望句子既要正向输入,也要反向输入,分别计算隐状态,再进行融合。但这个模型的应用场景有限制,需要我们拥有全文语料,像实时机器翻译这种场景就不合适,因为并不知道后文。
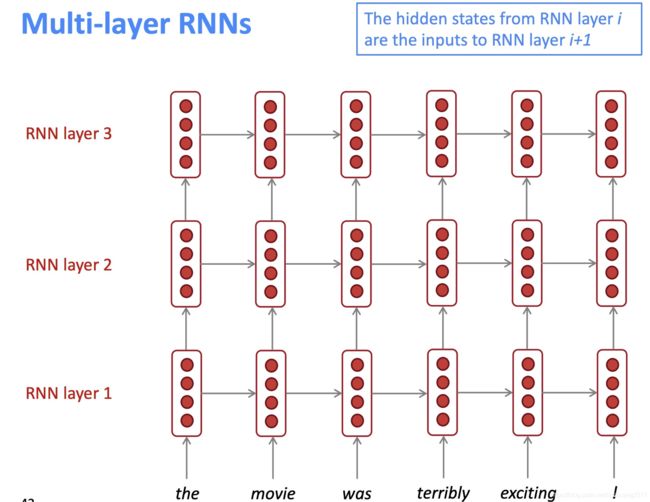
2. 多层RNN
在另外一个维度堆叠参数,可以帮助网络学习到更深层的语义信息,如果作为编码器,一般是堆2~4层,作为解码器一般堆4层,如果还需要更深,则可能需要用到跳层连接或者像densenet那样的密集连接。
六、参考文献
- CS224 Lecture 7 slides & notes
- http://colah.github.io/posts/2015-08-Understanding-LSTMs/
- https://zhuanlan.zhihu.com/p/109519044
- https://weberna.github.io/blog/2017/11/15/LSTM-Vanishing-Gradients.html
- [https://www.zhihu.com/question/34878706/answer/665429718](