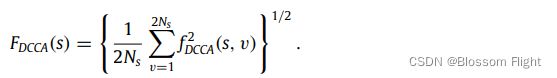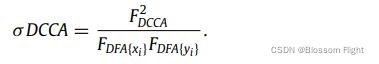DCCA互相关系数 理论
Cross-correlation analysis of stock markets using EMD and EEMD 源自2.4小节
DCCA方法是由Podobnik和Stanley[31]最近提出的,用于分析同时记录的非平稳时间序列之间的幂律互相关系,是互相关系研究的有力候选工具。因此,在以往的许多研究中,DCCA方法被用来研究相互关系[33-40]。DCCA过程可以简单描述如下:
考虑这两个时序:![]() 和
和![]() ,i=1,2,...,N,并且两时序长度相等为N。
,i=1,2,...,N,并且两时序长度相等为N。
σDCCA方法如下:
1. 序列概况可以表示为:
![]()
ps:减去均值不是必须的,因为在第三步去趋势部分会消除。
2. 对X和Y等长度划分s个不重叠的部分,一共![]() 个,
个,![]() =[N/s],而N可能不是时间尺度s的倍数,因此会出现剩余的情况,为了能考虑这个余部序列,同样的过程从每个时序【即X和Y】的另一端开始重复,因此可以得到2
=[N/s],而N可能不是时间尺度s的倍数,因此会出现剩余的情况,为了能考虑这个余部序列,同样的过程从每个时序【即X和Y】的另一端开始重复,因此可以得到2![]() 个小段。
个小段。
ps:本文设定100 3. 由每个序列的最小二乘拟合,计算2 第一个式子是正向的,先循环每个 第二个式子是反向的。 4. 对所有分段求平均,得到波动函数: 5. 通过分析 λ=0.5 缺乏互相关 λ>0.5 有持续的长期的互相关 λ<0.5 有反持续互相关 当只分析一个时间序列时( 为了量化互相关的程度,我们可以应用DCCA互相关系数[32],定义为比率在去趋势协方差函数 上式将我们引入了非平稳时间序列的一种新的互相关尺度。σDCCA取值范围为 -1<=σDCCA<=1。σDCCA = 0表示序列之间不存在互相关,σDCCA = 1表示完全互相关,正相关,σDCCA = -1表示负相关。值得注意的是,有一个例外,如果 参考文献: [31] B. Podobnik, H.E. Stanley, Detrended cross-correlation analysis: a new method for analyzing two nonstationary time series, Phys. Rev. Lett. 100 (2008) 084102. [32] G.F. Zebende, DCCA cross-correlation coefficient: Quantifying level of cross-correlation, Physica A 390 (2011) 614–618. [33] B. Podobnik, D. Horvatic, A.M. Petersen, H.E. Stanley, Cross-correlations between volume change and price change, Proc. Natl. Acad. Sci. USA 106 (2009) 22079–22084. 30 [34] W.X. Zhou, Multifractal detrended cross-correlation analysis for two nonstationary signals, Phys. Rev. E 77 (2008) 066211. [35] B. Podobnik, I. Grosse, D. Horvatic, S. Ilic, P.Ch. Ivanov, H.E. Stanley, Quantifying cross-correlations using local and global detrending approaches, Eur. Phys. J. B 71 (2009) 243–250. [36] Z.Q. Jiang, W.X. Zhou, Multifractal detrending moving average cross-correlation analysis, Phys. Rev. E 84 (2011) 016106. [37] A. Lin, P. Shang, X. Zhao, The cross-correlations of stock markets based on DCCA and time-delay DCCA, Nonlinear Dynam. 67 (2012) 425–435. [38] A. Lin, P. Shang, H. Zhou, Cross-correlations and structures of stock markets based on multiscale MF-DXA and PCA, Nonlinear Dynam. 78 (2014) 485–494. [39] D. Horvatic, H.E. Stanley, B. Podobnik, Detrended cross-correlation analysis for non-stationary time series with periodic trends, Europhys. Lett. 94 (2011) 18007. [40] I. Gvozdanovic, B. Podobnik, D. Wang, H.E. Stanley, 1/f behavior in cross-correlations between absolute returns in a US market, Physica A 391 (2012) 2860–2866 [41] X. Zhao, P. Shang, Y. Pang, Power law and stretched exponential effects of extreme events in Chinese stock markets, Fluct. Noise Lett. 9 (2010) 203–217. [42] J. Xia, P. Shang, J. Wang, Estimation of local scale exponents for heartbeat time series based on DFA, Nonlinear Dynam. 74 (2013) 1183–1190.![]() 小段每个的局部趋势,后续由
小段每个的局部趋势,后续由![]() 和
和![]() 表示。然后计算原始时间序列与拟合多项式的差值:
表示。然后计算原始时间序列与拟合多项式的差值: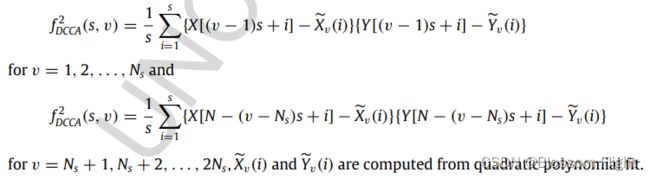
![]() 小段里的时序i,再循环外部分的
小段里的时序i,再循环外部分的![]() 小段。
小段。![]() 与s的对数曲线图,确定波动函数的缩放行为:
与s的对数曲线图,确定波动函数的缩放行为:![]() 。缩放指数λ表示两个时间序列
。缩放指数λ表示两个时间序列 ![]() 和
和![]() 之间的互相关程度。
之间的互相关程度。
![]() =
= ![]() ),去趋势协方差
),去趋势协方差![]() 退化为
退化为![]() 。λ指数量化了长期幂律互相关[41,42],但λ不能量化互相关水平。
。λ指数量化了长期幂律互相关[41,42],但λ不能量化互相关水平。![]() 和去趋势方差函数
和去趋势方差函数![]() 之间,即:
之间,即:![]() 和
和![]() ,都是随机序列,则σDCCA = 1,但两个随机序列不存在互相关关系。DCCA互相关系数在很多情况下都有应用。
,都是随机序列,则σDCCA = 1,但两个随机序列不存在互相关关系。DCCA互相关系数在很多情况下都有应用。