智能优化算法——正余弦优化算法（SCA）及其改进策略

一、基本介绍

1. 背景

近十年涌现了众多优秀的智能优化算法，然而一个算法在某些优化问题上的优异表现并不能保证其在其他问题上的有效性，即不存在一个算法能有效解决所有的优化问题，即著名的“无免费午餐”定理。

同时，新算法的提出是否能跳出仿生的思路而开拓新的思路也是我们的研究方向之一。正余弦算法的提出者 归纳了仿生智能优化算法的迭代策略并利用简单的正余弦函数逻辑构思出了正弦余弦算法(SCA) ，这也极大拓宽了开发新算法的思路。

2. 算法简介

SCA是一种新颖的随机优化算法，该算法最显著的特点是其通过简洁明了的形式完备了一个智能优化算法所应具备的必要要素，其仅利用正弦和余弦函数的波动性和周期性作为实现算子的设计目标来搜索和迭代最优解。与遗传算法，粒子群算法，等众多智能优化算法相比，正弦余弦算法具有参数少、结构简单、易实现、收敛速度快等优点，在实际应用中具有较优的性能。

正弦余弦算法(SCA）归纳吸收了部分群智能优化算法的迭代策略，以包含特定个数随机解的集合作为算法的初始解集,重复地通过目标函数评价解的适应度并按照特定更新策略随机迭代解集，最终求得最优解或满足适应度要求的满意解。同大部分群智能优化算法一样，SCA 依靠迭代策略实现解空间的随机搜索，并不能保证在一次运算中找到最优解，但当初始解集规模和迭代次数足够大时,求得最优解的概率大大提高。

二、基本的SCA算法

1. 算法介绍

SCA把迭代策略归纳结构为全局搜索和局部开发两个线程。
在全局搜索线程中，对当前解集中的解施加较大的随机波动来搜索解空间中的未知区域
在局部开发线程中，对解集施加微弱的随机扰动来充分搜索当前解的邻域。

SCA 利用正弦、余弦函数的周期波动性构造了实现全局搜索和局部开发两个线程功能的迭代方程，通过该简洁的更新迭代方程来施加扰动并更新解集，具体的迭代方程分为以下正弦迭代或余弦迭代方程两种:

其中 表示当前迭代次数，$X_i^j(t)$ 表示个体 $i$ 在第 次迭代时的位置在第 $j$ 维 的分量， $r_1$， $r_2$ ， $r_3$ 为随即参数， $r_1$ 由更新函数确定， $r_2$ ~ $U[0,2\pi ]$ ， $r_3$ ⋳ $(0,\infty )$，$P^j(t)$ 表示候选解集在第 次迭代的最优候选解在第 $j$ 维度的分量。

为了消除迭代步长和方向的相关关系，通过随即参数$r_4$ ~ $U[0,1]$ 将上面的两个迭代方程结合到完整的迭代方程：

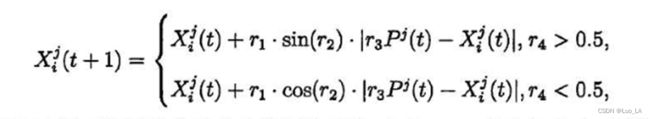
• $r1$ 控制算法从全局搜索到局部开发的转换。当 $r1$ 的值较大时，算法倾向于全局搜索；当 $r1$ 的值较小时，算法偏向于局部 开发。
• $r2$描述了当前解向当前最优解更新时移动的方向，以及所能达到迭代步长的极值,影响更新解是位于当前解及最优解之间的解空间还是之外的空间;
• $r3$ 为最优解给出一个随机权值，是为了随机强调( $r3$ ＞ 1 或者忽略( $r3$ ＜ 1 ) 最优解在定义候选解移动距离时的影响效果;
• $r4$ 描述了在正弦更新和余弦更新之间的随机性，拟消除迭代步长和方向可能存在的相关性。

以二维随机变量为例：
当 $r_{1}sin(r_2)$ 或 $r_{1}cos(r_2)$ 的值在 -1 和 1 之间时，迭代应用局部开发策略，算法搜索候选解和当前最优解之间的解空间，即侯选解的某个邻域； $r_{1}sin(r_2)$ 或 $r_{1}cos(r_2)$ 的值 $>1$ 或者 $<-1$ 时，则应用全局开发策略.SCA 正是借此实现了对解空间全局搜索和局部开发.

考虑到全局搜索和局部开发两个过程的平衡性和算法收敛到全局最优解的必要性，随着迭代的进行适应性地调整 $r_1$：
$$r_1=a-\frac{a}{T}t$$

$a$是一个常数; $t$ 为当前迭代次数; $T$ 为最大迭代次数; 由于 $r_1$ 的值随迭代次数逐渐减小，平衡了算法局部开发和全局搜索的能力;
当我们设置 $a=2$ 时，如图下图所示,此时 $r_{1}sin(r_2)$ 和 $r_{1}cos(r_2)$ （正余弦参数部分）的波动幅度随着迭代次数的增加逐渐衰减，其值在 $(1,2]$ 和 $[-2,-1)$ 范围内，算法进行全局搜索，在$[-1，1]$之间进行局部开发。

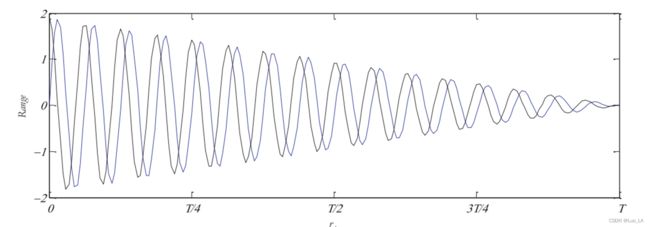
2. 算法步骤

1. 初始化迭代次数 $t=0$ ，初始候选解集 $m$，候选解随机位置 $X_i^j(t)$，迭代更新方程的 $r_1，r_2$等参数；
2. 计算每个候选解的适应度，确定并保留当前最优候选解 ()；
3. 根据迭代方程更新候选解集；
4. 根据公式和参数概率分布规律迭代更新方程的 $r_1，r_2$等参数；
5. 终止检验。判断终止条件是否满足，如达到迭代次数或满意解条件，则输出()；不满足则回到步骤 2。
   

三、算法分析

1. 正余弦分布

迭代式上下两个式子各以 0.5 的概率选取，由于正弦函数平移后便可以得到余弦函数，所以正弦函数和余弦函数的 函数值分布是相同的。因此，虽然 $r_2$ ~ $U[0,2\pi ]$ 是随机数，但是从概率角度而言，$r_{1}sin(r_2)$ 和 $r_{1}cos(r_2)$ 的函数值分布几乎相同。 取 $a=2,T=10000,r_1=a-at/T,r_2\in U[0,2\pi ]$， 下给出了 $r_2$ ~ $U[0,2\pi ]$ 函数值的频数分布直方图。

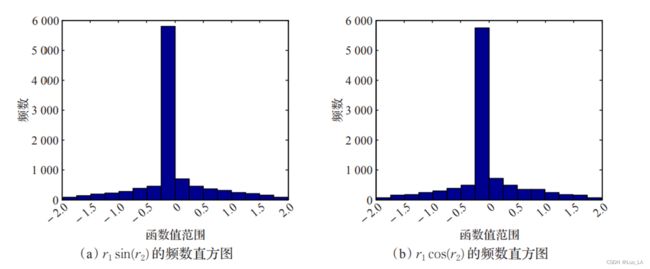
我们可以看出
$r_{1}sin(r_2)$ 和 $r_{1}cos(r_2)$ 频数直方图几乎是等效的。结合此图和$r_1$的计算公式，我们也可以发现，当迭代次数到达一定频数后，$r_1<1$，即算法后期不再进行全局搜索，而是局部开发。

2. 算法实验结果

在原论文中，研究人员试图在尽可能多的测试用例上测试他们的算法。本文采用了三组不同特性的测试函数。
所使用的案例研究包括单模态、多模态和复合测试函数。第一组测试函数没有局部最优值，只有一个全局最优值。这使得它们非常适合于测试算法的收敛速度和开发。第二组测试函数除了全局最优外，还有多个局部解。这些特征有利于测试算法的局部最优避免和探索能力。最后，复合测试函数是几个单模态和多模态测试函数的旋转、移位、偏置和组合版本。

为了求解上述测试函数，总共允许30个搜索代理在500次迭代中确定全局最优。将SCA算法与萤火虫算法(FA)、蝙蝠算法(BA)、花授粉算法(FPA、引力搜索算法(GSA）、粒子群算法(PSO)和遗传算法进行了比较，验证结果。由于元启发式的随机性质，单次运行的结果可能不可靠，所有算法都运行了30次，统计结果(均值和标准差) 如表所示。结果在[0,1]中进行了归一化，以比较所有测试函数的结果。

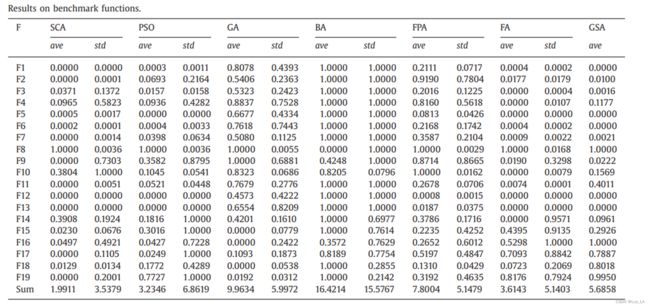
表中的结果表明，SCA算法在大多数测试用例中都优于其他算法。SCA算法在6个单模态测试函数中有3个显示出较好的结果。在所有的多模态测试函数上比其他算法表现得都要好（7，9，11，12），表1的最后一行给出了算法在所有测试函数上的平均值和标准差的总和。很明显，SCA的ave和std的都是最小的，证明该算法在总体上可靠地优于其他算法。

3. 算法优缺点

SCA 在候选解集规模和迭代次数充分的情况下求解优化问题的全局最优解的理论优势在于:

• SCA同其他群智能优化算法一样，相对单个候选解的算法，一定规模的候选解集实现了更强的搜索能力和逃离局部最优陷阱能力，具有充分的随机搜索能力；
• 最优候选解在迭代过程中始终被保留并作为更新候选解集的依据，在搜索过程中有向最优解空间移动的趋势；
• SCA全局搜索和局部开发的随机性与分两阶段进行搜索和开发相比具有更强的适应性和稳定性；
• SCA 的随机搜索设计使其具有广泛的适用性,能求解不同领域不同类型的优化问题。

其测试函数集的表现也说明了其存在的一些不足：

• SCA 在部分测试函数上具有一定的早熟情况，受到一些较明显的局部最优陷阱的影响;；
• SCA最终求解的满意度围绕理论最优解波动较大，算法的收敛性有待提高。

四、SCA改进策略

1. 参数的改进

第一类改进策略研究了转换参数 $r_1$ 对 SCA 全局搜索和局部开发两个线程平衡的影响，提出了参数$r_1$非线性递减的正余弦算法，实现了算法计算精度和收敛速度一定程度的提高。其测试了凸函数中的抛物线函数和凹函数中的指数函数来作为$r_1$的更新策略:

$$抛物线函数：r_1=a(1-\frac{t}{T}{)}^2，指数函数：r_1=a{e}^{-\frac{t}{T}}$$

转换参数非线性递减的 SCA算法流程仅参数 $r_1$ 同标准SCA 不同，算法流程同与SCA相同。

2. 应用权重更新机制

为了改善迭代过程中父代个体的信息具有惯性权重所导致的搜索后期震荡性，提出了应用个体适应度调整的权重更新机制的正余弦算法（WSCA）
在WSCA 中,除了当前最优解及扰动幅度，每个候选解还受到一个按其适应度线性调整的权重的影响,该权重取决于其在候选集中适应度的排序值，适应度较高的候选集分配较高的权重，在更新过程中对一下代候选解集影响较大:

$$W_{x_i(t)}=1-i\times (\frac{1}{m})$$

其中 表示当前迭代次数，$x_i(t)$ 表示第 次迭代中适应度第高的候选解， $W_{x_i(t)}$ 表示在 次迭代中$x_i(t)$所获得的权重，$m$表示候选解集规模。

在确定每个候选解的权重之后再选择一部分适应度较高的候选集计算平均位的分量:

$$Au{g}_i^j=\frac{sum(W_{x_1(t)}{x}_1(t),W_{x_2(t)}{x}_2(t),...,W_{x_c(t)}{x}_c(t))}{c_t}$$

其中$c_t$为参与平均位置计算的优选候选解的规模,随迭代次数的增加而减少，$c_t=[m-\frac{1}{m}t]$

以上的权重机制(WUPM)着眼于消除迭代过重中候选解的惯性权重所可能导致的算法后期震荡性，WSCA候选解迭代更新方程如下:

根据上式,一方面,算法初始所有候选解都参与平均位置的计算,描述了算法进行全局搜索的随机性;随着迭代次数的增加,只有适应度较高的候选解参与平均位置的计算,适应度较低的候选解对迭代策略的影响越来越小。另一方面,迭代过重中适应度较低的候选解的权重越来越小,平均位置最终只保留当前最优解,算法充分开发当前最优解的邻域并最终求得问题的全局最优解.算法的流程如下:

1. 初始化迭代次数 $t=0$，粒子群$m$，候选解随机位置 $X(t)$，优选候选解规模 $c$ ，迭代更新方程初始参数等;
2. 计算候选解集中候选解及反向目标的适应度，选取适应度较高的$m$个组成新的候选解集 ；
3. 计算当前平均候选解的所有分量 $Aug$；
4. 根据上面方程更新候选解集；根据迭代次数更新参数$r_1，r_2，c_t$等;
5. 终止检验。判断终止条件是否满足,如迭代次数或满意解条件,则输出$X(t)$。不满足则回到步骤2。

3. 基于反向学习的改进

将优化启发式算法收敛性常用的反向学习（OBL）运用到SCA当中并提出了反向学习正余弦算法（OBSCA）。OBL改进策略考虑了候选解在解空间对称位置的解的信息并在迭代过程中保留适应度较高的一方,以可接受的计算成本提高算法的有效程度和收敛性.

OBL 策略首先定义实数 $x\in [1,u]$ 的反向数 $\bar{x},\bar{x}=l+u-x$，则多维变量$X=(x_1,x_2,\dots ,x_n)\in R^n,x^i\in [l_i,u_i]$的反向目标 $\bar{X},$ 可定义为：
$$\bar{X}=(\bar{x}1,{\bar{x}}_2,\dots ,{\bar{x}}_n)，{\bar{x}}_i=l_i+u_i-x_i,i=1,2,\dots n$$

基于反向目标的定义, 对于$m$个候选解的候选解集$M$,计算$M$中每个候选解$X$和其反向目标的适应度,保留两个集合中适应度最高的$m$个解组成新的候选集$M$,完成候选解的反向学习.将OBL 整合到SCA 中,在每次迭代过程对当前候选解集应用OBL 得到适应度较高的新候选解集M之后再依据标准SCA迭代公式更新候选解集,就得到了OBSCA.OBSCA的算法流程如下:

1. 初始化迭代次数$t=0$，粒子群$m$，候选解随机位置 $X(t)$，优选候选解规模$c$ ，迭代更新方程初始参数等;
2. 计算每个候选解的适应度，按适应度递减排序，确定每个候选解的权重；
3. 迭代候选解集；
4. 更新参数$r_1，r_2$等;
5. 终止检验。判断终止条件是否满足,如迭代次数或满意解条件,则输出$X(t)$。不满足则回到步骤2。

引入反向 学习策略增加了可选粒子数量，并择优选取粒子，增大随机性的同时提高种群进化速度。通过可接受的计算成本增加较好地提高了算法的收敛性和准确性。

五、引用与代码

参考论文：Mirjalili S.SCA：a sine cosine algorithm for solving optimization problems
代码：python实现SCA算法