Fermat素性检测算法(Python实现)

说明
这是某电的网信院密码学实验1

一、实验目的（包括实验环境、实现目标等等）

1. 实验环境

• Windows11
• PyCharm2019.3.3 x64

2. 实现目标

• 通过编写代码实现Fermat素性检验算法，加深对Fermat素性检验算法的理解，体会该算法在解决实际问题的价值；
• 将密码学和数学知识相联系，并灵活运用到密码学的设计方案中；
• 提高实践能力和逻辑思维能力

二、方案设计（包括背景、原理、必要的公式、图表、算法步骤等等）

1. 实验背景

Fermat素性检验算法基于费马小定理提出。

2. 实验原理

(1)给定素数p, a∈Z，则有a^p-1 ≡ 1(mod⁡ p);
(2)奇整数m, 若任取一整数2 ≤ a ≤ m - 2, (a, m) = 1, 使得a^m-1 ≡ 1(mod ⁡m)，则m至少有$\frac{1}{2}$的概率为素数。

3. 算法步骤

给定奇整数m ≥ 3和安全参数k：
(1)随机选取整数a, 2 ≤ a ≤ m - 2;
(2)计算g = (a, m), 如果g = 1，转(3); 否则，跳出，m为合数;
(3)计算r = a^m-1 (mod ⁡m), 如果r = 1，m可能是素数，转(1); 否则跳出，m为合数;
(4)重复上述过程k次，如果每次得到m可能为素数，则m为素数的概率为1 - $\frac{1}{2^k}$ .

三、方案实现（包括算法流程图、主要函数的介绍、算法实现的主要代码等等）

1. 流程图

2. 主要函数

• quick_mod(num1, num2, num3)：实现快速模指数运算的函数；其中num1为底数，num2为指数，num3为除数
• math.gcd(a, m)：math 模块里判断两个数是否互素的函数
• random.randint(2, m - 2)：random 模块里的生成随机数的函数

3. Python代码

import random
import math


def quick_mod(num1, num2, num3):
    result = 1
    while num2 > 0:
        if (num2 & 1) == 1:
            result = (result * num1) % num3
        num1 = (num1 * num1) % num3
        num2 = num2 >> 1
    return result


m = int(input("请输入您要检测的数m:"))
k = int(input("请输入安全参数k: "))
i = 1
while i <= k:
    a = random.randint(2, m - 2)
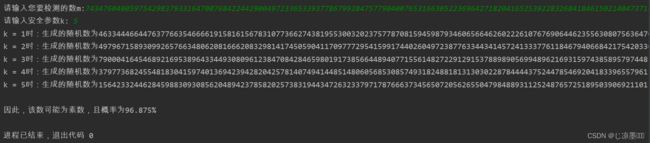
    print("k = " + str(i) + "时：生成的随机数为" + str(a), end="，")
    g = math.gcd(a, m)
    r = quick_mod(a, m - 1, m)
    if g != 1:
        print("(%d,%d) = %d，该数为合数!" % (a, m, g))
        break
    elif r != 1:
        print("%d**%d(mod %d) = %d，该数为合数!" % (a, m - 1, m, r))
        break
    else:
        print("m = " + str(m) + "可能为素数!")
        i += 1


if i == k + 1:
    print("\n因此，该数可能为素数，且概率为" + str((1 - 1 / (2 ** k)) * 100) + "%")

4. 其它

位运算：n & 1（判断n是否为奇数）：因为n为奇数时，对应的二进制数最低位一定为1，n & 1的结果就是1；n为偶数时，相应的最低位为0，n & 1的结果就是0

四、数据分析(包括算法测试数据的分析，运行结果截图等等)

1. 测试数据1

743476040059754298379331647007684224429004972336533937786799284757790400765316630522369642718204165253922832684184615021404737105614714107158733905598636152327037707290538422718453498125366750918857659068838460954633737911274770976191590193809661578032117496009853673140977556559136466107768672598883924301125589893895001253674886100289402530711221893

运行结果：

2. 测试数据2

5434520625653357625890820149570485819447986258433769976634917091398967074086679540928507095017715540385352266035820823142060119390272763774034231321959236056764511968630360067353876686142517564224926196131349204754111599877101485686283117193149781387816214484583521923017500621725053392290279263586984207169423800476914654441473576611460323772832328657

运行结果：

3. 测试数据3

876147742992673125957404768949712978720573116974723188491435550196169965040848206868200084918233743662847668000971402407461887306389122707315529364807593342507936022301657320206278702095378618110195051280478534126716517153056984269659532882692418682262081495725304483536777013188527470348249542840277926802938912332306310470632601156641005608958891

运行结果：

4. 测试数据4

9876147742992673125957404768949712978720573116974723188491435550196169965040848206868200084918233743662847668000971402407461887306389122707315529364807593342507936022301657320206278702095378618110195051280478534126716517153056984269659532882692418682262081495725304483536777013188527470348249542840277926802938912332306310470632601156641005608958891

运行结果：

五、思考与总结

1. 如果有一个整数，(, )=，使得⁻ ≡ 则一定是一个素数吗？为什么？（请简述并举例说明，不能只简单回答“是”或“不是”）

答：不一定。假如a = 8, m = 63，a和m互素，并且满足8^63-1 ≡ 8⁶² = (8²)³¹ ≡ 1(mod ⁡63)，也就是a^m-1 ≡ 1(mod ⁡m)，但是m并不是素数。

2、Fermat素性检测中都用到了哪些运算？分别实现什么功能？请简述。

答：（1）用到了求模运算，主要是解决算法的第3步骤：计算r = a^m-1 (mod⁡ m)，如果r = 1，m可能是素数，转(1)；否则跳出，m为合数；
（2）生成随机数，主要为了解决算法的第3步：随机选取整数a，2 ≤ a ≤ m - 2；
（3）判断两个数是否互素，主要解决算法第2步，为之后的运算做判断：计算g = (a, m)，如果g = 1，转(3)；否则，跳出，m为合数。

3、 你还了解哪种素性检测算法？请简述，并分析其与Fermat素性检测算法的区别与联系。

答：米勒—拉宾素性检验（Miller-Rabin Test），它在费马素性检测的基础上又添加了另外的判断条件。相同点：它和费马素性检测算法一样只能判断一个数字是合数还是可能是素数。也就是说，费马小定理只是一个数m是素数的必要条件，即：费马小定理不成立，m一定是合数；费马小定理成立，m可能是素数。此算法的优点：给出的结果是错误结果的概率小于等于$\frac{1}{4}$，如果反复测试k次，则错误的概率可以降至($\frac{1}{4}$)^k，这是一个很保守的估计，因此使用的效果在一定程度上比Fermat更好。