优化| 手把手教你学会杉树求解器(COPT)的安装、配置与测试
优化| 手把手教你学会杉数求解器COPT的安装、配置与测试
-
- 前言
-
- 线性规划(LP)测试榜单--单纯形法： Benchmark of Simplex LP solvers
- 线性规划(LP)测试榜单--内点法： Benchmark of Simplex LP solvers
- 混合整数规划(MIP)测试榜单
- COPT的申请、安装、配置和测试
-
- COPT的许可(license)以及安包申请
- COPT的安装
- COPT许可配置
- COPT求解优化模型的测试： python接口
- 参考资料
作者： 刘兴禄，清华大学，清华伯克利深圳学院博士在读
欢迎关注我们的微信公众号 运小筹
前言
最近杉数求解器发布了4.0.2版本。著名的优化求解器benchmark测评的官网也更新了最近的榜单。
网址如下：
Benchmarks for Optimization Software - Hans Mittelmann
http://plato.asu.edu/bench.html
线性规划(LP)测试榜单–单纯形法： Benchmark of Simplex LP solvers
单纯形法目前COPT排名第一，阿里的MindOpt紧随其后，Gurobi排名第三。COPT略微领先于MindOpt。COPT、MindOpt、Gurobi是榜上唯三的解决了所有的40个问题的3个求解器。
线性规划(LP)测试榜单–内点法： Benchmark of Simplex LP solvers
内点法目前COPT也是在榜单中排名第一，Gurobi紧跟其后，差距非常小。
混合整数规划(MIP)测试榜单
MIP的benchmark数据集有3个，如下图所示。
我们只看第一个，也就是MILP Benchmark - MIPLIB2017 (2-5-2022)。
根据结果可知，在MILP Benchmark - MIPLIB2017 (2-5-2022)测试榜单中，Gurobi稳居第一，以较大优势领先其他求解器。 COPT排名第二，跟Gurobi任然有一些差距。运行速度方面
- 在单线程
(1 thread)：Gurobi：COPT = 1: 4.19； - 在8线程
(8 threads)：Gurobi：COPT = 1: 3.50。
可见COPT目前速度也已经慢慢具有较强的竞争力，大家可以去愉快地尝试使用了。小编也是期待了很久，最近也决定尝试学习和使用COPT了。
看完了这些，我们来进入主题，开始COPT的安装、配置和测试。
COPT的申请、安装、配置和测试
COPT的许可(license)以及安包申请
同学们可以在下面的网址填写信息申请License和安装包，目前网址不支持直接下载安装包。COPT会通过邮件的方式将安装包和license发送给你。
申请网址： https://www.shanshu.ai/copt
申请界面如下：
注意事项：
申请界面的用户账号， 需要通过上图中如何获取用户账号名称里面的方法获得，不要想当然的乱写，否则申请测license是不匹配的。
- 如果用学校的邮箱申请。license是365天。
- 如果是用自己的163,qq, gmail等邮箱申请，License的有效期是6个月。
这是之前用163邮箱申请的情况
这是用学校邮箱申请的情况
COPT的安装
上图提供了两个链接，分别是
https://pub.shanshu.ai/download/copt/4.0.2/win64/CardinalOptimizer-4.0.2-win64-installer.ziphttps://pub.shanshu.ai/download/copt/4.0.2/win64/CardinalOptimizer-4.0.2-win64.zip
建议下载第二个，这个比较方便。原因是：第二个不用自己配置环境变量，COPT在安装的过程种会自动地配置环境变量。
下载之后，我们解压安装即可。
安装界面就是一直next就好，这里不再赘述。
COPT许可配置
COPT必须要配置相应的许可文件才能正常使用。license就在回复你的邮件中，如下图所示
配置许可的方法就是
- 以管理员身份打开命令行
win+R + cmd- 切换到COPT的安装目录下，如果你没有修改目录的话，默认目录是
C:\Program Files\COPT"，我们执行命令cd C:\Program Files\COPT- 执行命令:
copt_licgen -key 你的license，例如
copt_licgen -key copt_licgen -key 19200817f147gd9f60abc791def047fb
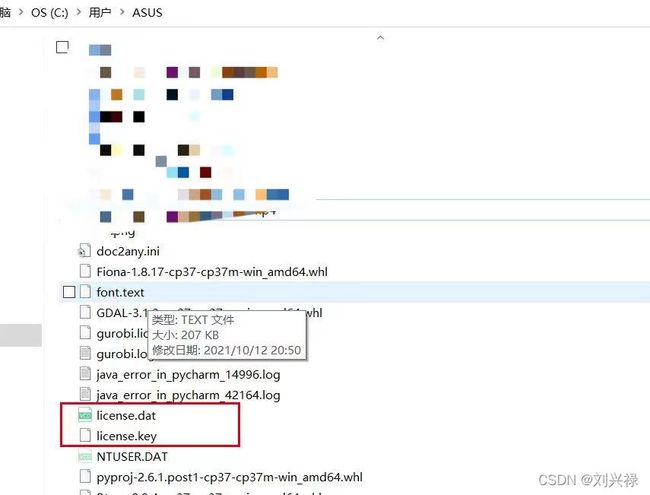
注意中间的空格。- 执行完毕后，你的用户根目录下会自动生成两个授权文件:
license.dat和license.key
这两个文件你可以通过搜索找到，也可以直接到相应目录下去找。我的电脑是在这里
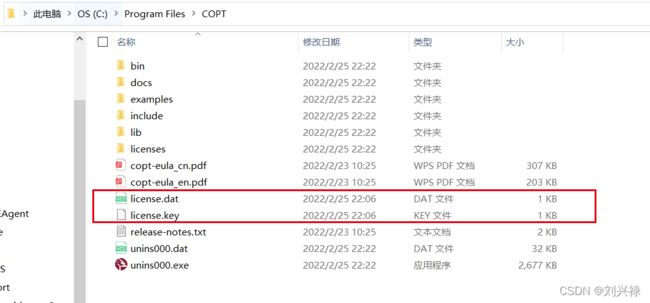
- 完成这一步，别忘了最后一步。将
license.dat和license.key拷贝到COPT的安装目录下，也就是拷贝到C:\Program Files\COPT"下。如下图。大功告成！可以开始写代码了。
COPT求解优化模型的测试： python接口
我们用一个非常简单的线性规划模型来测试一下。
例子如下：
max 8 x 1 + 5 x 2 s . t . x 1 + x 2 ⩽ 6 9 x 1 + 5 x 2 ⩽ 45 x 1 , x 2 ⩾ 0 \begin{aligned} \max \quad & 8x_1 + 5x_2 \\ s.t. \quad & x_1 + x_2 \leqslant 6 \\ & 9x_1 + 5x_2 \leqslant 45 \\ & x_1, x_2 \geqslant 0 \end{aligned} maxs.t.8x1+5x2x1+x2⩽69x1+5x2⩽45x1,x2⩾0
Python调用COPT建模的程序跟其他求解器基本一致，但是不同于Gurobi，COPT需要首先创建一个环境(也就是创建一个Envr 类的实例)，然后用这个Envr实例，调用函数createModel来建立模型。下面是一个例子：
from coptpy import *
# Create COPT environment
env = Envr()
# create model
model = env.createModel("LP example")
建模过程主要用到的函数如下：
- 创建环境+创建模型：
Envr()和Envr.createModel(name) - 创建决策变量:
Model.addVar(lb=0.0, ub=COPT.INFINITY, obj=0.0, vtype=COPT.CONTINUOUS, name="", column=None) - 设置目标函数：
Model.setObjective(expr, sense=None) - 添加约束：
Model.addConstr(lhs, sense=None, rhs=None, name="") - 创建线性表达式:
LinExpr(arg1=0.0, arg2=None)
– 注意，COPT中，LinExpr对象的addTerm()函数，第一个位置是系数(coef)，第二个位置是变量(var)，比如
–expr = LinExpr();
–expr.addTerm(1, x_1)； - 求解模型：
Model.solve()（注意，目前4.0.2版本及更早的版本，暂时还不支持callback。） - 设置求解参数(求解时间，Gap等)：
Model.setParam(paramname, newval)
– 设置求解时间：m.setParam(COPT.Param.TimeLimit, 3600)
– 设置求解MIP的求解Gap：model.setParam(COPT.Param.RelGap, 0.1) - 输出目标值：
model.objval - 输出解的值和变量名
–Model.getVars():获得模型的所有变量；
–var.index：获得变量的index，这个不同于变量名，只是一个序号；
–var.x: 获得变量在最优解中的取值；
–var.getName(): 获得变量名。
下面我们来完整地写出上面的例子并求解，输出解的信息。完整代码如下：
from coptpy import *
# Create COPT environment
env = Envr()
# create model
model = env.createModel("LP example")
# create variables
x1 = model.addVar(lb=0, ub=COPT.INFINITY, vtype = COPT.CONTINUOUS, name="x1")
x2 = model.addVar(lb=0, ub=COPT.INFINITY, vtype = COPT.CONTINUOUS, name="x2")
# create objective
model.setObjective(8*x1 + 5*x2, sense=COPT.MAXIMIZE)
# create constraints
model.addConstr(x1 + x2 <= 6)
model.addConstr(9*x1 + 5*x2 <= 45)
# solve and output the optimal solution
model.solve()
print("Objective value: {}".format(model.objval))
print("Variable solution:")
for var in model.getVars():
print(" x[{0}]: {1}".format(var.index, var.x))
求解结果如下
Hardware has 8 cores and 16 threads. Using instruction set X86_NATIVE (1)
Maximizing an LP problem
The original problem has:
2 rows, 2 columns and 4 non-zero elements
The presolved problem has:
2 rows, 2 columns and 4 non-zero elements
Starting the simplex solver using up to 8 threads
Method Iteration Objective Primal.NInf Dual.NInf Time
Dual 0 7.0451048183e+01 2 0 0.01s
Dual 2 4.1250756485e+01 0 0 0.01s
Postsolving
Dual 2 4.1250000000e+01 0 0 0.01s
Solving finished
Status: Optimal Objective: 4.1250000000e+01 Iterations: 2 Time: 0.01s
Objective value: 41.25
Variable solution:
x[0]: 3.75
x[1]: 2.25
从上述求解日志和求解结果来看，COPT使用了对偶单纯形法(dual simplex)求解该问题，迭代了2步。
COPT的建模语法、求解日志信息与其他求解器（例如Gurobi）也是类似的风格，用户学习成本极低。
开心，接下就可以进一步研究更多的用法了。之后有空我会陆续推出基于COPT的推文。希望对大家有帮助。
参考资料
[1]: 杉数科技官网: https://www.shanshu.ai/copt
[2]: 杉数求解器用户手册4.0.2.
欢迎关注我们的微信公众号 运小筹
公众号往期推文如下
